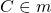Формулировка серединный перпендикуляр к отрезку или медиатриса звучит так — прямая, прочерченная через середину стороны под углом 90 0 .
- Характерные особенности медиатрисы треугольника.
- Характерные особенности средней линии треугольника.
- Как построить высоту треугольника — основные способы
- С применением циркуля
- С помощью линейки
- В остроугольном треугольнике
- В тупоугольной фигуре
- В прямоугольном и равнобедренном
- Серединный перпендикуляр
- 🎬 Видео
Видео:Перпендикулярные прямыеСкачать

Характерные особенности медиатрисы треугольника.
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Правильна будут и такая формулировка: любая точка, равноудаленная от концов отрезка, размещена на серединном перпендикуляре к нему.
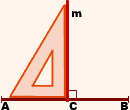
Центр описанной окружности находится в месте пресечения медиатрис треугольника. Следует отметить, что у остроугольного треугольника эта точка размещается внутри, у тупоугольного — за пределами треугольника, у прямоугольного — посредине гипотенузы.
Средняя линия трехугольника – отрезок, соединяющий середины двух его сторон. Общеизвестно, что у треугольника три стороны, и логично, что и три средние линии.
MN, MК, КN — средние линии для треугольника ABC.
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Характерные особенности средней линии треугольника.
Средняя линия трехугольника всегда параллельна одной из сторон и равна 1/2 этой стороны.
Средняя линия отделяет трехугольник, который подобен первоначальному, а их площади соотносятся ¼.
При пересечении всех трёх средних линий образуются четыре одинаковых треугольника, подобных первоначальному, но с коэффициентом подобия 0,5.
Видео:Построение серединных перпендикуляров треугольника с помощью циркуляСкачать

Как построить высоту треугольника — основные способы
Видео:Перпендикуляр от точки к плоскостиСкачать
С применением циркуля
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.
Способ начертить искомый отрезок:
- На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
- Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
- Иглу циркуля ставят в вершине любого угла у основания.
- Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
- Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
- Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
- Делают пометку в месте пересечения начерченных окружностей.
- Ластиком стирают лишние линии, оставляя лишь поставленную точку.
- С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
- Стирают линии, находящиеся под основанием.
Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.
Видео:7 класс, 16 урок, Перпендикуляр к прямойСкачать

С помощью линейки
Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.
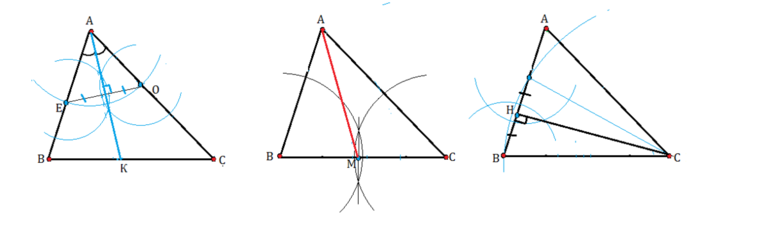
В остроугольном треугольнике
Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.
Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.
Правильная последовательность действий:
- Находят вершину, из которой хотят провести перпендикуляр.
- Совмещают угольник с противоположной стороной фигуры.
- Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
- Простым карандашом проводят линию, которая и будет искомым отрезком.
В тупоугольной фигуре
Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.
Порядок действий:
- Располагают чертёж так, чтобы тупой угол оказался у основания.
- Угольник прикладывают к наибольшей стороне фигуры.
- Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
- Соединяют 2 точки простым карандашом, получая искомую линию.
В прямоугольном и равнобедренном
В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.
Пошаговая инструкция:
- Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
- Вторую сторону линейки совмещают с вершиной прямого угла.
- Проводят линию, которая будет высотой.
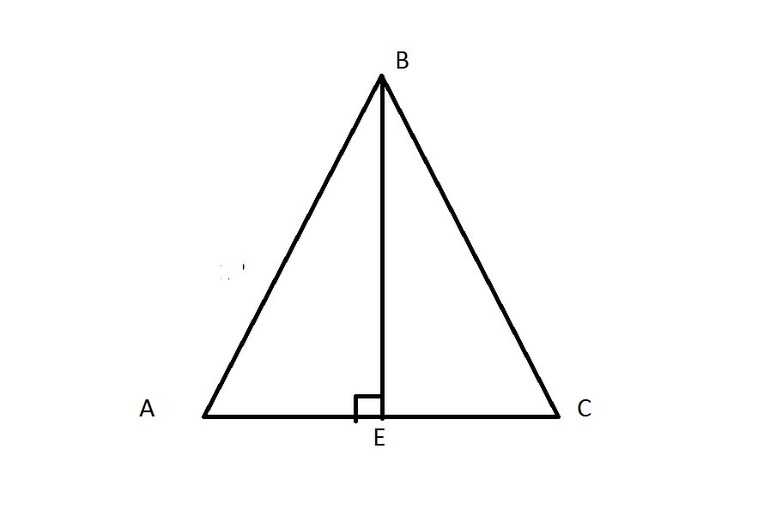
Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.
Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:
- Линейкой замеряют длину основания.
- Эту величину делят на 2.
- Полученное значение откладывают от вершины одного из углов при основании.
- Отмечают середину стороны и соединяют её с верхней точкой фигуры.
Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.
Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.
Видео:Построение высоты в треугольникеСкачать

Серединный перпендикуляр
Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.
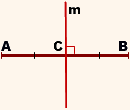
m — серединный перпендикуляр к отрезку AB, если
точка C — середина отрезка AB,
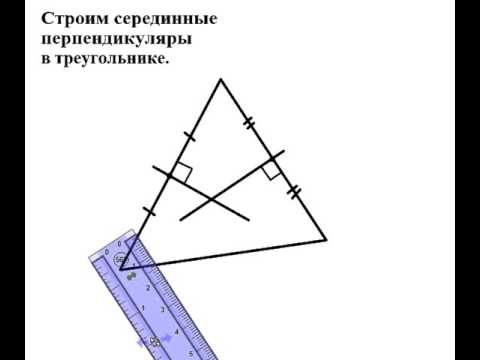
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:
1) найти середину отрезка;
2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):
Свойства серединного перпендикуляра.
1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.
3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
🎬 Видео
Геометрия 7 класс (Урок№11 - Перпендикуляр к прямой.)Скачать

Наклонная, проекция, перпендикуляр. 7 класс.Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

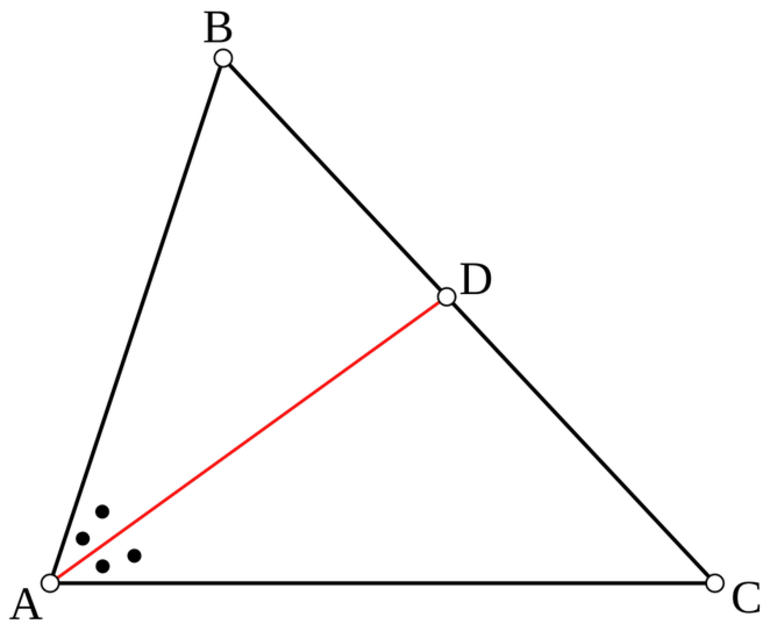
№258. Из середины D стороны ВС равностороннего треугольника ABC проведен перпендикулярСкачать

Перпендикулярные прямые. 6 класс.Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

Перпендикуляр к прямой через заданную точку.Скачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Построение перпендикуляра к прямойСкачать

Урок 12. Серединный перпендикуляр к отрезку (7 класс)Скачать

Серединные перпендикуляры в треугольникеСкачать
КАК ПРОВЕСТИ СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР? #shorts #егэ #огэ #математика #профильныйегэ #перпендикулярСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать