Вычисление длины дуги окружности в ворде информатика

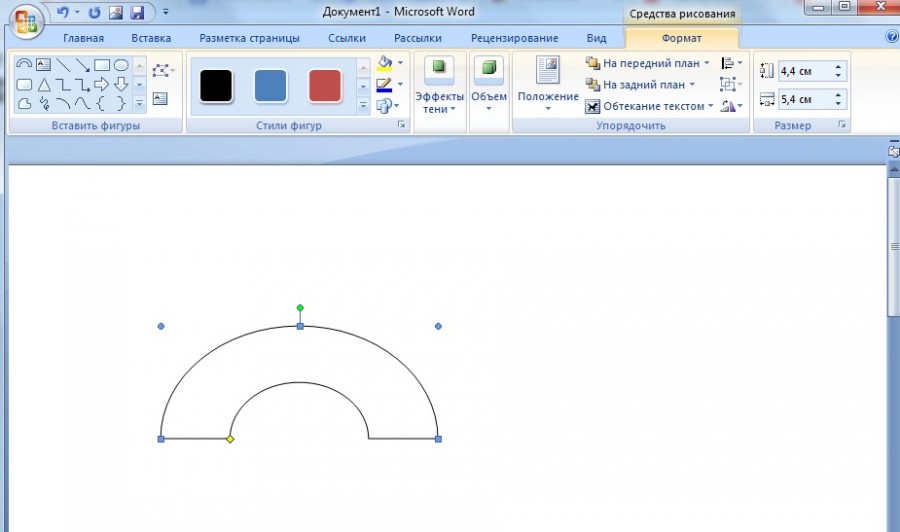
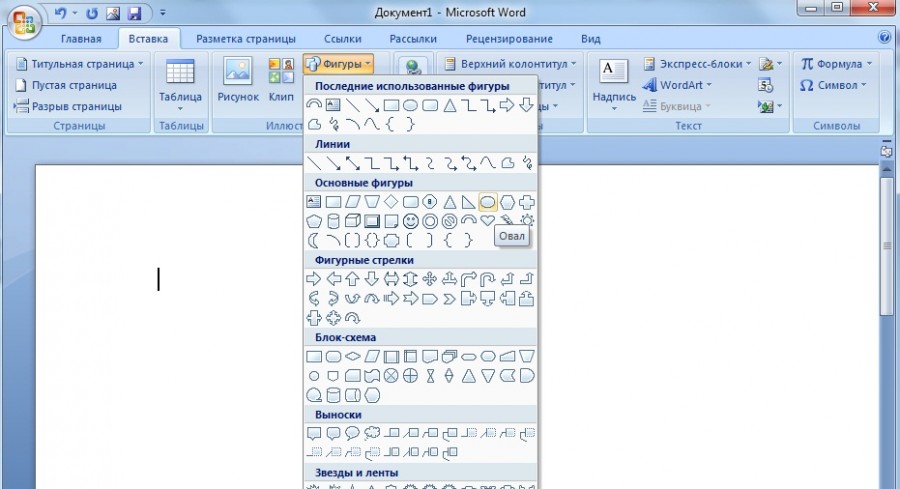
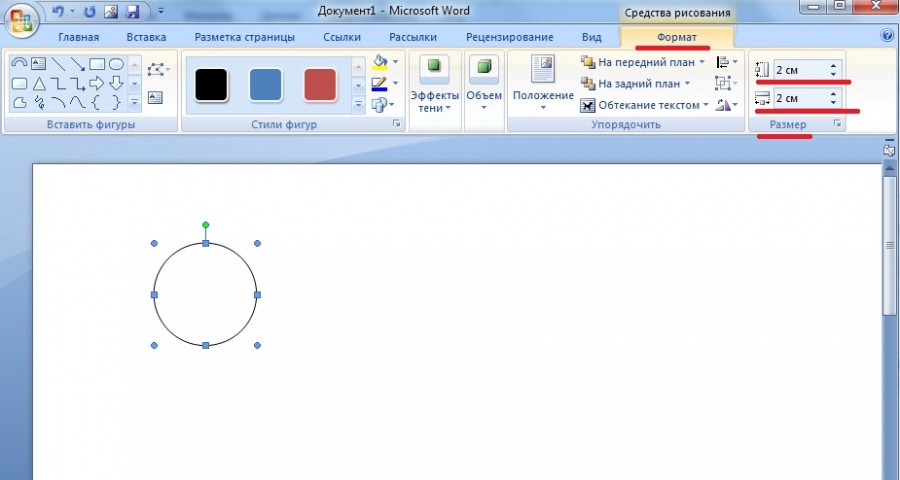
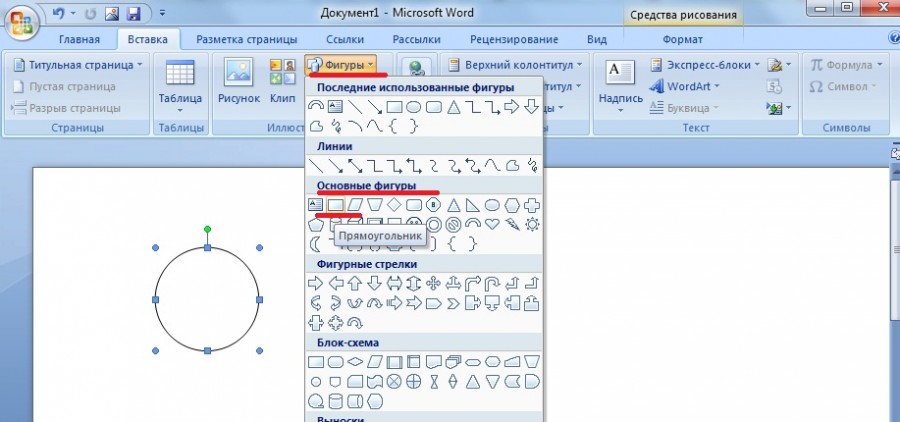
В программе ворд существует два способа нарисовать полукруг, давайте рассмотрим каждый более подробный.

Первый способ.

Первый шаг. На верхней панели настроек программы ворд, заходим во вкладку «Вставка», где в блоке «Иллюстрации» нажимаем на иконку «Фигуры». После чего откроется меню с разнообразными фигурами и в разделе «Основные фигуры», находим иконку «Арка» и жмем на неё.

Второй шаг. На экране появляется специальный крестик, и рисуем полукруг, потом можем его выделить и уменьшить или увеличить его размер и границы.

Второй способ.

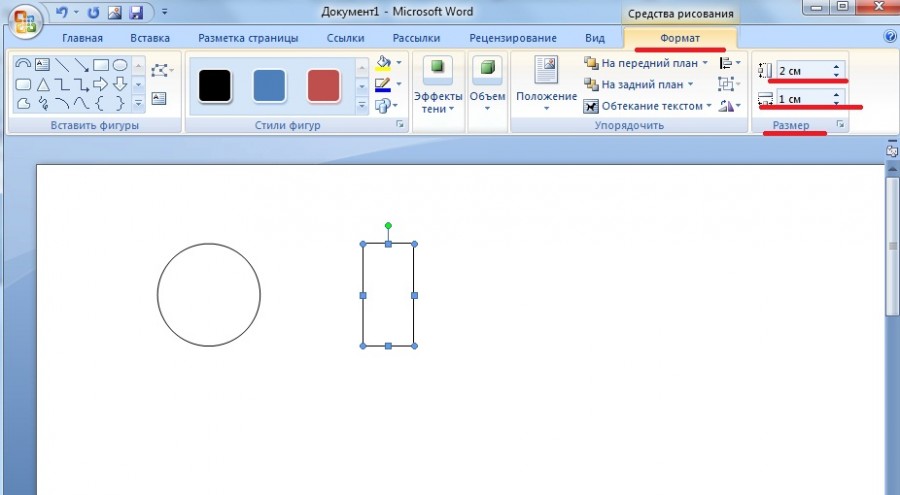
Первый шаг. Снова заходи во вкладку «Вставка», нажимаем на иконку «Фигуры» и в разделе «Основные фигуры» выбираем овал и рисуем сначала в произвольном размере.

Второй шаг. После этого выделяем овал и на верхней панели в закладке «Формат» устанавливаем размер ширины и высоты по два сантиметра.

Третий шаг. Снова входим во вкладку «Вставка», нажимаем на иконку «Фигуры» и в разделе «Основные фигуры», выбираем прямоугольник.

Четвертый шаг. Нарисовав прямоугольник произвольного размера, выделяем его. И задаем высоту два сантиметра, а ширину один сантиметр.

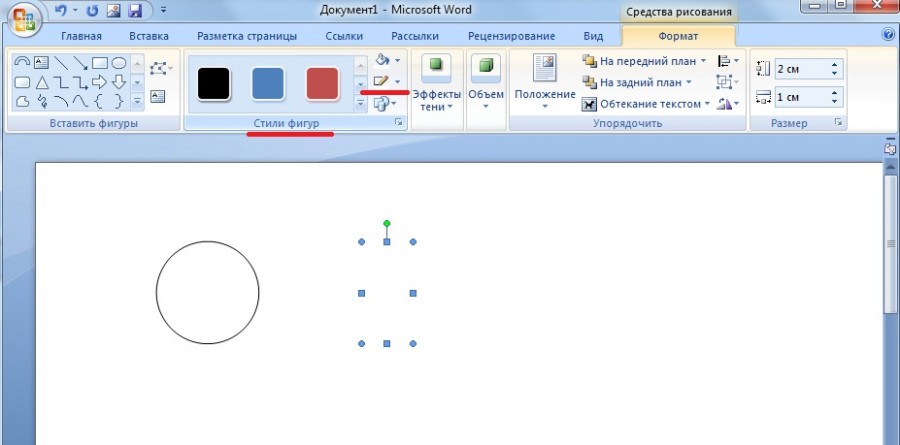
Пятый шаг. Теперь на панели «Формат», находим блок «Стили фигур» и выбираем белый цвет контура.

Шестой шаг. Теперь перемещаем прямоугольник, накладывая его на круг, в итоге мы получим полукруг.

Видео:Нахождение длины дуги кривойСкачать

Видео.

Видео:Длина дуги окружности. 9 класс.Скачать

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»
методическая разработка по информатике и икт (9 класс) на тему

Занятие, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Практическая работа на тему

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»

В данной разработке представлены задачи с геометрическим содержанием по теме «Окружность и круг» для 9 класса. Для этих задач разработаны алгоритмы и программы на псевдокоде и языке Паскаль. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе.

Видео:Вычисление длины дугиСкачать

Скачать:

Видео:ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать

Предварительный просмотр:

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС »

учитель математики информатики

Видео:Длина дуги кривойСкачать

Введение

Одна из главная задач ФГОС, которые призваны реализовать развивающий потенциал общего среднего образования — готовить своих учеников к жизни, обеспечить ребенку общекультурное, личностное и познавательное развитие, вооружить умением учиться. Перед выпускниками, вступающими в самостоятельную жизнь, встаёт проблема решать новые, неизвестные задачи, которые неизбежно встанут перед ними. Результат образования можно «измерить» умением успешно решать такие задачи.

В новых стандартах метапредметным результатам уделено особое внимание, поскольку именно они обеспечивают более качественную подготовку учащихся к самостоятельному решению проблем, с которыми встречается каждый человек на разных этапах своего жизненного пути в условиях быстро меняющегося общества. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе. Программирование обучает методам мышления, общим подходам к постановке и решению задач. Поэтому выбрана тема занятия, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Видео:Длина дуги кривой| Урок 1| Надежда Павловна МедведеваСкачать

Основная часть

Тема занятия : Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг».

Видео:Длина дуги окружностиСкачать

Задания, которые рассматриваются на занятии:

• вычисление длины окружности по заданному радиусу;
• нахождение площади круга, ограниченного окружностью заданного радиуса;
• нахождение площади кольца по внутреннему и внешнему радиусам;
• вычисление расстояния между двумя точками с заданными координатами;
• найти площади сектора по радиусу и дуге;
• определение минимального радиуса круга, в который попадают точки, заданные координатами на плоскости;

Для решения задач используем линейные структуры, ветвления и циклы.

Видео:Окружнось, дуга, длина дуги, центральный угол.Скачать

Проверяемые элементы содержания

Формальное исполнение алгоритма, записанного на естественном языке или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд.

Знание основных конструкций языка программирования, понятия переменной, оператора присваивания.

Умение исполнить алгоритм для конкретного исполнителя с фиксированным набором команд.

Анализ алгоритма, содержащего вспомогательные алгоритмы, цикл и ветвление.

Умение анализировать результат исполнения алгоритма.

Видео:Нахождение длины дуги кривой.Скачать

Основное содержание теоретической части

Алгоритмы работы с величинами: константы, переменные, понятие типов данных, ввод и вывод данных.

Структура программы на языке Паскаль. Представление данных в программе. Правила записи основных операторов: присваивания, ввода, вывода, ветвления, циклов.

Этапы решения задачи с использованием программирования: постановка задачи, формализация, алгоритмизация, кодирование, отладка, тестирование.

Практика на компьютере: знакомство с системой программирования на языке Паскаль; ввод, трансляция и исполнение данной программы; разработка и исполнение линейных, ветвящихся и циклических программ.

Переменная, константа, операторы ввода/вывода, оператор присваивания, арифметические операции с переменными.

Создание с использованием свойств геометрических фигур математических моделей для решения задач практического характера и задач из смежных дисциплин (для данного занятия – конкретно геометрии), исследовать полученные модели и интерпретировать результат.

Задачи на применение линейных алгоритмических структур. В ходе решения задач повторяются формулы курса геометрии 9 класса: вычисление длины окружности, площади круга, площади кольца, площади сектора, расстояния между двумя точками на плоскости, заданных координатами (метод координат в курсе геометрии).

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Задания на этапе первичного закрепления

Рассмотрим подробно задачи геометрического содержания с постановкой, математической моделью, алгоритмом, программой на языке Паскаль и полученными результатами (скриншот).

Задача 1. Вычислить длину окружности по заданному радиусу.

1. Результат – найти длину окружности.
2. Исходные данные – радиус окружности.
3. Ограничения на результат – положительное число.
4. Ограничения на исходные данные – положительное число.

Математическая модель. Вычислить длину окружности по формуле

Описать переменные. Ввести данные.

Вычислить по формуле длины окружности C= 2*π*R.

Write( ‘Введите радиус окружности R= ‘ );

WriteLn( ‘Длина окружности С= ‘ ,C: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 37, 57344814. Верно.

Задача 2. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

1. Результат – площадь круга.
2. Исходные данные – длина окружности.
3. Ограничения на результат – положительное число.
4. Ограничения на исходные данные – положительное число.

Математическая модель. Выразить радиус R из формулы длины окружности C= 2*π*R. Вычислить радиус R=C/(2* π). Вычислить площадь круга по формуле S= .

Описать переменные. Ввести данные.

Выразить радиус R из формулы длины окружности.

Вычислить радиус по формуле R=C/(2* π). Вычислить площадь круга по формуле S= .

Write( ‘Введите длину окружности С= ‘ );

WriteLn( ‘Площадь круга = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверка результата с помощью калькулятора, получим число 426, 5116724. Значит, программа правильна.

Задача 3. Найти площадь кольца, внутренний радиус которого равен r, а внешний – заданному числу R (R> r).

1. Результат – найти площадь кольца.
2. Исходные данные – внутренний радиус равен r, а внешний – R (R> r).
3. Ограничения на результат – положительное число.
4. Ограничения на исходные данные – положительные числа.

Математическая модель. Найдём площадь кольца по формуле S к =π*(R*R-r*r), где – R — внешний радиус, r-внутренний радиуc, (R> r).

Описать переменные. Ввести данные.

Вычислить по формуле площадь кольца по формуле S к =π*(R*R-r*r).

Writeln( ‘Введите радиусы окружностей R2 и R1 ‘ );

S := pi * (R2 * R2 — R1 * R1);

WriteLn( ‘Площадь кольца S = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 12, 56637061. Верно.

Задача 4. Вычислить расстояние между двумя точками с координатами X1, Y1 и X2, Y2.

1. Результат – найти расстояние R между двумя точками на плоскости.
2. Исходные данные – даны координаты точек (X1, Y1) и (X2, Y2).
3. Ограничения на результат – ограничение на расстояние R>=0
4. Ограничения на исходные данные — ограничений на координаты нет.

Математическая модель. Выведем формулу для вычисления расстояния между двумя точками на плоскости.

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x b — x a ;
BC = y b — y a .

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости: AB = .

Описать переменные. Ввести данные.

Вычислить расстояние между точками по формуле R= .

Напишем алгоритм на псевдокоде

* вывод (‘Введите координаты (x и y) точки 1’)

* вывод (‘Введите координаты (x и y) точки 2’)

* R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

* вывод (‘расстояние между точками 1 и 2 равно ‘, R:10:3);

X1, X2, Y1, Y2, R: Real ;

Writeln( ‘Введите координаты (x и y) точки 1’ );

Writeln( ‘Введите координаты (x и y) точки 2’ );

R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

Write( ‘расстояние между точками 1 и 2 равно ‘ , R: 10 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 4. Верно.

Задача 5. Найти площадь сектора, радиус которого равен 15.4, а дуга содержит заданное число радиан ϕ .

1. Результат – площадь сектора.
2. Исходные данные – величина угла в радианах.
3. Ограничения на результат – положительное число.
4. Ограничения на исходные данные – значение дуги в радианах меньше, чем 2π ≈ 6.28. Иначе сектор будет по величине больше круга.

Модель. Выведем формулу для вычисления площади сектора через угол, выраженный в радианах. Сектор круга ограничивается дугой между двумя точками А и В на окружности и двумя радиусами, проведёнными из концов дуги (точек А и В) к центру круга.

Два радиуса делят всю площадь круга на 2 сектора. Если угол между этими радиусами будет развёрнутым (180 0 ), то эти секторы будут между собой равны. Площадь сектора круга – это часть площади всей плоской фигуры, ограниченной окружностью с радиусом r. Площадь круга равна произведению квадрата радиуса на число S= . Площадь кругового сектора в радиан (полукруга) равна . Поэтому площадь сектора в один радиан в π раз меньше, т.е. равна : π. Значит, площадь сектора в α радиан равна =

* вывод (‘Введите величину дуги кругового сектора (в радианах)’)

* вывод (‘Площадь кругового сектора =’, S:8:2)

write(‘Введите величину дуги кругового сектора (в радианах) ‘);

writeln(‘Площадь кругового сектора = ‘, S:8:2)

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора.

Задача 6. Даны координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn,yn). Определить минимальный радиус круга, в который попадают все эти точки. Центр круга находится в начале координат.

1. Результат – определить минимальный радиус круга, в который попадают точки с заданными координатами.
2. Исходные данные – координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn, yn).
3. Ограничения на результат – неотрицательное действительное число.
4. Ограничения на исходные данные – координаты точек выражаются действительными числами, количество точек N — натуральное число.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И МЕТОД: Радиус круга с центром в начале координат вычисляется по формуле R= . Для наглядности рисунок.

АЛГОРИТМ. Вычисляем радиус (расстояние от начала координат до точки) для каждой точки, выбираем минимальное значение. Сравниваем два числа, наименьшее значение записываем как минимум. Это и будет минимальным значением радиуса. Так как количество точек известно, организуем цикл с параметром.

Видео:Видеоурок "Длина дуги кривой"Скачать

Компьютерный практикум. Создание текстовых документов. MS Word

Источники информации

УМК «Информатика» Л.Л. Босовой, А.Ю. Босовой, 10-11 классы. Информатика. Компьютерный практикум.

Цели работ. Отработка навыков в текстовом процессоре:

• ввод текста с клавиатуры;
• редактирование и форматирование фрагментов текста;
• автоматический контроль орфографии;
• создание и оформление многоуровневых списков, таблиц, формул, векторных изображений.

Просмотр содержимого документа
«Компьютерный практикум. Создание текстовых документов. MS Word»

Ввод, редактирование и форматирование документа. Создание списков и таблиц. Создание формул и рисунков.

Задание 1. Создайте и оформите текст «Основные элементы текстового документа» в соответствии с приведённым ниже образцом.

выравнивание — по центру;

шрифт — Аrial Вlаск;

размер шрифта — 16;

выравнивание — по ширине;

шрифт — Times New Roman;

размер шрифта — 14;

красная строка — 1 см;

междустрочный интервал всего текста — одинарный.

Место для выполнения задания 1

Задание 2. Убедитесь в отсутствии ошибок в созданном документе, используя средства орфографического контроля. (Рецензирование  Правописание)

Скопируйте первый набранный текст. Вставьте скопированный фрагмент в документ.

Для первой копии фрагмента используйте следующие параметры форматирования:

междустрочный интервал — 1,5 строки;

число колонок — Две.
(Выделите текст  вкладка Разметка страницы  Колонки Две)

Место для выполнения задания 3

Скопируйте и вставьте первый набранный текст.

Для второй копии фрагмента используйте следующие параметры форматирования:

отступ первой строки — нет;

междустрочный интервал — одинарный;

интервал перед абзацем — 24 пт;

первые символы абзацев — Буквица:
Пояснение:

Выделите символ  Вставка  Буквица Параметры буквицы:

интервал перед — 6 пт.

высота в строках: 2;

Место для выполнения задания 4

Вставьте копию первого набранного текста.

Для второй копии фрагмента используйте следующие параметры форматирования:

отступ слева — 2 см, справа — 2 см;

для первых слов абзацев интервал шрифта — разреженный на: 2пт;

текст абзацев в рамке,

заливка — голубая.
Пояснение:

Место для выполнения задания 5

Отформатируйте текст ниже по образцу.

выравнивание — по центру;

шрифт — Courier New;

размер шрифта — 14.

выравнивание — по ширине;

отступ слева — 1 см;

шрифт — Courier New;

размер шрифта — 14;

междустрочный интервал — одинарный.

ПРАВИЛА ПОСТАНОВКИ ПРОБЕЛА

Пробел используют только как разделитель между словами. Клавишу «ПРОБЕЛ» между словами надо нажимать только один раз.

после разделительных знаков (. , : ; ! ?) ; до и после тире;

перед открывающими кавычками или скобками; после закрывающих кавычек или скобок; перед знаками процентов;

в числе между цифрами, обозначающими сотни и тысячи, тысячи и миллионы ит. п.;

перед и после знаков арифметических операций, логических операций и операций отношения.

Пробел не ставится:

перед разделительными знаками (. , : ; ! ?); до и после дефиса;

перед закрывающими кавычками или скобками; после открывающих кавычек или скобок; перед знаками минут, секунд; в обыкновенных дробях;

после знаков «+» и «-» при записи положительных и отрицательных чисел.

Создайте и оформите многоуровневый список «Основные виды рефератов» в соответствии с приведённым ниже образцом.

выравнивание — по центру;

тип начертания — полужирный;

шрифт — Times New Roman;

размер шрифта — 11;

цвет шрифта — чёрный;

выравнивание — по левому краю;

шрифт — Times New Roman;

размер шрифта — 14;

междустрочный интервал — одинарный.

Преобразуйте текст в список

ОСНОВНЫЕ ВИДЫ РЕФЕРАТОВ

По полноте изложения

Количество реферируемых источников

Характер подачи информации (переработки знаний)

По читательскому назначению

Рефераты, составленные специалистами.

Воспроизведите по представленному ниже образцу сетку первого современного кроссворда, созданный в 1913 году американским журналистом Артуром Уинном.

💡 Видео

Вычисление длины дуги кривой в параметрических и полярных координатах. Вычисление объема тела.Скачать

Математика это не ИсламСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

Вычисление площадей плоских фигур в полярных координатах. Вычисление длины дуги кривой(продолжение).Скачать

8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Длина окружности. Математика 6 класс.Скачать

Учитель: Серікбол Актоты Тема урока: Формула длины дуги окружностиСкачать

Как создать многоуровневый списокСкачать

Master Arc Length Calculation Effortlessly With The Pipe Trades Pro Calculator!Скачать