В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин — точка O.
а) Докажите, что около четырёхугольника ABCD можно описать окружность.
б) Найдите радиус вписанной окружности, если AC = 10, BD = 26.
а) Рассмотрим треугольники ABO и COD: углы ABD и BDC при секущей BD не равны. Тогда, так как треугольники ABO и COD подобны, следовательно, углы ABO и DCO, а также BAO и CDO равны. Аналогично для треугольников AOD и BDC. Сумма углов ABO и OBC не равны 90°, тогда имеем конфигурацию как на рисунке справа.
Заметим, что сумма углов BAD и BCD равна:
Следовательно, вокруг четырехугольника ABCD можно описать окружность.
б) Обозначим сторону BO буквой a, сторону OC буквой b, тогда:
Из этого следует, что стороны AO и OC равны.
Пусть OB равно x, тогда
при 
С учетом симметрии, можно выбрать любое значение для x. Пусть OB равно 1, а OD — 25, тогда:
Найдем полупериметр четырехугольника ABCD:
Найдем площадь четырехугольника ABCD:
Вычислим искомый радиус:
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:№43. Диагонали четырёхугольника ABCD пересекаются в точке M. Известно, что углы BAC и ADC прямыеСкачать  Диагонали четырехугольника авсд пересекаются в точке о под прямым угломЗадание 16. В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке О под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин — точка О. а) Докажите, что в четырёхугольник ABCD можно вписать окружность. б) Найдите радиус вписанной окружности, если АС = 12, BD = 13. а)В четырехугольнике ABCD диагонали AC и BD взаимно перпендикулярны и пересекаются в точке O, следовательно, Пусть и это означает, что в четырехугольник ABCD можно вписать окружность. б)Радиус r вписанной окружности можно найти из площади четырехугольника ABCD: где P – периметр четырехугольника ABCD. Отсюда следует, что Рассмотрим равнобедренный треугольник ABC с биссектрисой OB, которая также является его высотой и медианой. Следовательно, AO=OC=6. Рассмотрим прямоугольный треугольник BCD с прямым углом Решаем квадратное уравнение, получаем корни: То есть, BO=4, OD = 9 или, наоборот, BO=9, OD=4. Возьмем первый вариант. Тогда: Следовательно, И радиус вписанной окружности, равен: Ответ: Видео:№1039. Диагонали квадрата ABCD пересекаются в точке О. Найдите угол между векторами: а) АВ и АССкачать  Диагонали четырехугольника авсд пересекаются в точке о под прямым углом
В четырехугольнике ABCD противоположные стороны не параллельны. Диагонали четырехугольника ABCD пересекаются в точке О под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин – точка О. а) Докажите, что в четырехугольник ABCD можно вписать окружность. б) Найдите радиус вписанной окружности, если AC = 12, BD = 13.
Решение: а) Δ ABO = ΔCBOпо катету и острому углу (BO–общая сторона, ∠ АВО = ∠СВО — по условию ) → АВ = СВ и АО = СО; Δ ADO = ΔCDO по катету и острому углу (DO – общая сторона, ∠ АDО = ∠ СDО — по условию ) → АD = СD и АО = СО; Т.к. AB = CB и AD = CD, то AB + CD = CB + AD→ в четырехугольник ABCD можно вписать окружность. б) Т.к. АО = СО и АС = 12, то АО = СО = 6 Пусть BO = y, тогда DO = 13 — y По свойству пересекающихся хорд AO⋅CO = BO⋅DO: Если у = 4, то ВО = 4и DO = 9 Если у = 9, то BO = 9 иDO = 4 Если в четырехугольник можно вписать окружность, то его площадь равна S = pr, где p–полупериметр четырехугольника, S–площадь четырехугольника, r–радиус вписанной окружности. 📹 ВидеоГеометрия Диагонали четырехугольника ABCD пересекаются в точке O Известно что угол A = углу D AO=ODСкачать  №382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать  №402. Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольникиСкачать  Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать  ОГЭ без рекламы математика 11 и 12 вариант задача 25Скачать  Геометрия Диагонали прямоугольника ABCD (см. рис.) пересекаются в точке O, угол ABD = 64. НайдитеСкачать  Геометрия Диагонали грани ABCD куба ABCDA1B1C1D1 пересекаются в точке O Найдите угол между прямымиСкачать  Геометрия Диагонали прямоугольника ABCD (см. рис.) пересекаются в точке O, угол ADB = 30, BD = 10 смСкачать  №748. Диагонали параллелограмма ABCD пересекаются в точке O. Равны ли векторы?Скачать  Задание 3 (№27717) ЕГЭ по математике. Урок 80Скачать  №403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметрСкачать  №1040. Диагонали ромба ABCD пересекаются в точке О, и диагональ BD равна стороне ромба.Скачать  №552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать  7.41.1. Планиметрия. Гордин Р.К.Скачать  7.43.1. Планиметрия. Гордин Р.К.Скачать  ОГЭ 2020 задание 18Скачать  №771. В параллелограмме ABCD диагонали пересекаются в точке ОСкачать 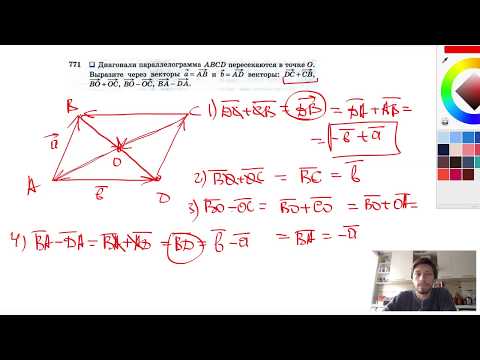 №511. В трапеции ABCD с боковыми сторонами АВ и CD диагонали пересекаются в точке О. а) Сравните плоСкачать  |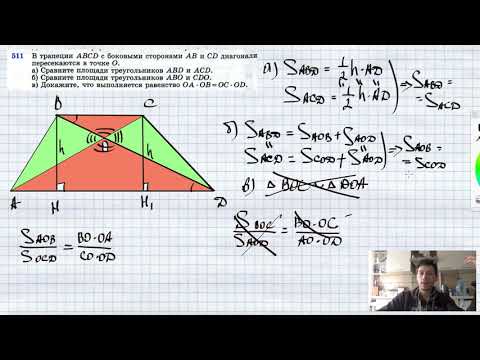
(так как треугольники ABO и CBO подобны по условию задания). Так как 
, то 
и 
. Так как треугольники BCOи COD подобны, то 
. Так как треугольники OCDи OADподобны, то 
. Треугольники ABC и ADC – равнобедренные со сторонами AB = BC и AD = DC. Следовательно,
. Следовательно, CO – высота. Пусть BO = y, тогда OD=13-yи
. Получаем периметр и площадь четырехугольника ABCD:
