Диагонали АС и ВD выпуклого четырёхугольника ABCD пересекаются в точке Р. Известно, что угол DAC равен 90°, а в 2 раза больше угла ADB. Сумма угла DBС и удвоенного угла ADС равна 180°.
а) Докажите, что ВР = 2AP.
б) Найдите площадь четырёхугольника AВCD, если BD = 8 и точка Р является серединой диагонали BD.
а) Пусть биссектриса угла РСВ пересекает отрезок РВ в точке М. Обозначим буквой β угол ADB. Получаем, что
Так как по свойству вертикальных углов, треугольники APD и МРС подобны, поэтому ∠PMC = 90°. Таким образом, в треугольнике ВСР биссектриса СМ является высотой, а значит, треугольник ВСР равнобедренный и PM = MB, CP = CB.
В треугольнике DBC:
Из этого равенства и из того, что следует, что ∠PCD = ∠PDC. Поэтому треугольник PCD равнобедренный и PD = PC. Значит, треугольники APD и МРС равны, поэтому
откуда следует, что BP = 2AP.
б) Точка Р является серединой отрезка BD, поэтому Отсюда следует, что треугольник ВСР равносторонний, поэтому ∠BPC = 60°. Из равенства
получаем, что AP = 2 и
Теперь найдём площадь четырёхугольника AВCD:
Ответ: б)
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать  Диагонали четырехугольника abcd ac и bd пересекаются в точке p найдитеЗадание 16. Диагонали АС и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC = CD. а) Докажите, что AB:BC=AP:PD. б) Найдите площадь треугольника COD, где О — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, АВ = 5, а ВС = 5√2. а) Так как стороны BC=CD, то и дуга BC равна дуге CD. На эти дуги опираются равные углы: BAC, CAD, CBD, CDB. Получаем подобные треугольники BPC и APD (по двум углам), следовательно, Далее, треугольники BPC и ABC также подобны по двум углам, поэтому В результате из (1) и (2), имеем: б) Так как BD – диаметр окружности, то треугольники BCD и ABD – прямоугольные с прямыми углами C и A соответственно. Также по условию задания BC=CD=5√2, получаем Рассмотрим прямоугольный треугольник BAD, в котором AB=5, BD=10, следовательно, угол BDA=30°, а угол ODO1 = 15° (так как O – центр вписанной окружности, поэтому DO – биссектриса). Далее, из равнобедренного треугольника BCD с основание BD получаем, что угол CDB=45°, следовательно, угол ODC=45+15=60°. Из прямоугольного треугольника ABD и полупериметр треугольника ABD, равен: Найдем отрезок DE=p-AB (как отрезок части касательной), имеем: и радиус вписанной окружности: Рассмотрим прямоугольный треугольник OED, из которого Рассмотрим треугольник OCD, в котором Ответ: Видео:Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать  В четырёхугольнике ABCD диагонали АС и BD перпендикулярны и пересекаются в точке Р. Отрезок, соединяющий вершину С с серединой МВидео:Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 12, AB = 7. Найдите DO.Скачать  Ваш ответВидео:№1040. Диагонали ромба ABCD пересекаются в точке О, и диагональ BD равна стороне ромба.Скачать  решение вопросаВидео:Геометрия Диагонали AC и BD трапеции ABCD пересекаются в точке O. Площади треугольников AOD и BOCСкачать  Похожие вопросы
Популярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 🌟 Видео№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать  Диагонали четырёхугольника ABCD, вписанного в окружность, взаимно перпендикулярны. Из вершин В и ССкачать 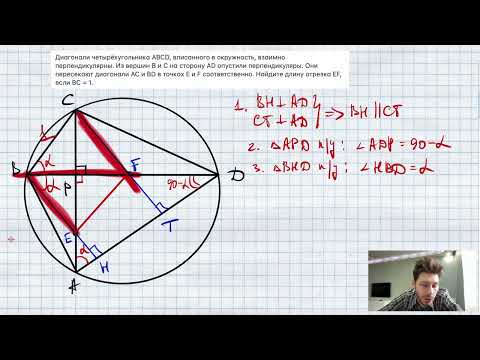 ОГЭ 2020 задание 18Скачать  Геометрия Диагонали четырехугольника ABCD пересекаются в точке O Известно что угол A = углу D AO=ODСкачать  #26. EGMO-2022, Problem 6Скачать  №403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметрСкачать  №912. Диагонали параллелограмма ABCD пересекаются в точке О, М - середина отрезка АО. НайдитеСкачать  ОГЭ по математике. Задание 15Скачать  Геометрия Диагонали четырёхугольника ABCD, вершины которого расположены на окружности, пересекаютсяСкачать  №383 На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что PB=QD. ДокажитеСкачать  Геометрия В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке P. Докажите, чтоСкачать  №43. Диагонали четырёхугольника ABCD пересекаются в точке M. Известно, что углы BAC и ADC прямыеСкачать  3.25.1. Планиметрия. Гордин Р.К.Скачать  ОГЭ по математике. Задание 16Скачать  ОГЭ 2022 Математика Задача №23 Вариант 5 Сборник под редакцией Ященко 36 вариантов.Скачать  |
 и
и или
или  (1)
(1)
 или
или  (2)
(2)







 , следовательно, треугольник ODC – равносторонний. Площадь этого треугольника, равна:
, следовательно, треугольник ODC – равносторонний. Площадь этого треугольника, равна:
