Окружности косоугольная диметрическая проекция (3 видео)

Pereosnastka.ru

Содержание

Обработка дерева и металла
Аксонометрические проекции
4.1. Прямоугольные проекции
4.1.1. Изометрическая проекция
4.1.2. Диметрическая проекция
4.2 Косоугольные проекции
4.2.1 Фронтальная диметрическая проекция
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
4.3.2 Построение эллипса по хордам
4.4 Штриховка сечений
Элементы косоугольной (фронтальной) диметрической проекции
🔍 Видео

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Обработка дерева и металла

Во фронтальной косоугольной диметрической проекции принято следующее положение аксонометрических осей: ось ох направлена горизонтально; ось оу — под углом 45° к оси ох и ось oz — вертикально . По этим осям и следует вести построение фронтальной проекции предмета. Допускается применять «левое» расположение осей.

Линейные размеры, параллельные оси оу, откладывают в масштабе, вдвое меньшем, чем по осям ох и oz. Характерным для этого вида аксонометрических проекций является то, что фигуры, параллельные фронтальной плоскости проекций V, изображаются без искажений. Поэтому такие аксонометрические проекции и называются фронтальными. Построение фронтальной проекции всегда начинают с нанесения осей, которые проводят тонкими сплошными линиями. Последовательность построения фронтальных проекций некоторых фигур показана на рис. 2.

Если расположить ось вращения цилиндра параллельно оси oz или ох, то его основания проецируются в виде эллипсов.

Фронтальная диметрическая проекция куба с вписанными в его грани окружностями изображена на рис. 34. Окружность, расположенная на передней грани куба, изображается без искажений, а окружности, расположенные на верхней и боковой гранях, изображаются в виде эллипсов одинаковой формы и размеров.

Для построения эллипса на гранях находят восемь точек, которые затем плавно соединяют по лекалу. Четыре точки определяются сразу — это середины сторон параллелограммов, изображающих грани куба. Четыре другие точки определяются на диагоналях параллелограммов путем переноса их с диагоналей квадрата.

Для построения эллипса на верхней грани сначала на передней грани куба отмечают точки 1 и 2 пересечения диагоналей квадрата с окружностью. Затем из этих точек проводят прямые параллельно оси oz до верхнего ребра куба (верхней стороны квадрата). Из полученных на ребре точек проводят прямые параллельно оси оу до пересечения их с диагоналями параллелограмма. Это и будут точки эллипса.

Аналогично находят диагональные точки при построении эллипса на боковой грани куба. Соединив найденные точки плавной кривой по лекалу, получим эллипсы.

Угол наклона большой оси эллипса равен примерно 7° по отношению к оси ох, если эллипс изображает окружность на верхней грани куба, и по отношению к оси oz, если эллипс изображает окружность на боковой грани куба. Малую ось эллипса располагают перпендикулярно большой.

На практике при построении фронтальных проекций деталей цилиндрической формы обычно вычерчивают не эллипсы, а овалы. Форма овала близка к форме эллипса, но вычертить его более просто, так как построение выполняют циркулем по правилам сопряжений.

Овал на верхней грани куба строят следующим образом: – проводят аксонометрические оси ох, оу и oz; затем из центра О — окружность диаметром, равным диаметру окружности, изображенной на рис. 34; – проводят большую ось овала под углом 7° к оси ох и перпендикулярно к ней малую ось. Продолжение малой оси пересекает окружность в точках O1 и 02; – из точек Oi и,02, как из центров, проводят вспомогательные дуги радиусом 001 равным 002, до пересечения с продолжением малой оси в точках 03 и 04, являющихся центрами больших дуг овала; – проводят прямые 04Л и 03В, которые пересекут большую ось овала в точках 06 и Ов, являющихся центрами малых дуг овала; – из центров 03 и 04 проводят большие дуги овалов радиусом 04А, равным 03В; – из центров 08 и 06 проводят малые дуги, замыкающие овал, радиусом ОьА, равным ОйВ.

Построение овала — приближенного изображения окружности — в профильной плоскости аналогичное.

Рассмотрим построение фронтальной диметрической проекции модели по чертежу, приведенному на рис. 5. Сначала проводят оси проекций ох, оу и oz. Наиболее характерным видом модели является вид спереди, поэтому построение фронтальной проекции начинают с вычерчивания в плоскости осей ох—oz такого же изображения, каким является вид спереди. В этой плоскости тонкими, едва заметными линиями намечают прямоугольник, соответствующий наибольшей высоте и ширине модели. Для этого по оси ох от точки о влево откладывают 60 мм (ширина модели), а по оси oz вверх — 40 мм (высота модели). Из полученных отметок проводят прямые, соответственно параллельные осям проекции ох и oz. Посередине габаритного прямоугольника проводят вертикальную осевую линию.

По отношению к этой осевой линии в габаритном прямоугольнике вычерчивают контур модели, соответствующий очертанию ее изображения на виде спереди. Из угловых точек вычерченного контура проводят параллельные прямые под углом 45° по отношению к оси ох, соответствующие направлению оси оу во фронтальной проекции.

На наклонных прямых откладывают размер толщины модели, уменьшенной в два раза, т. е. 50 : 2 = 25 мм. Полученные на наклонных прямых отметки соединяют последовательно прямыми линиями, в результате чего получают изображение модели во фронтальной проекции. Все указанные построения выполняют тонкими, едва заметными линиями. По окончании построения обводят полученное изображение контурными линиями и удаляют линии построения и линии невидимого контура.

Видео:Диметрические проекции.Скачать

Аксонометрические проекции

Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими .

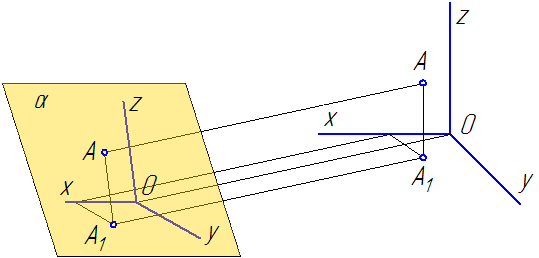
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1p/

Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
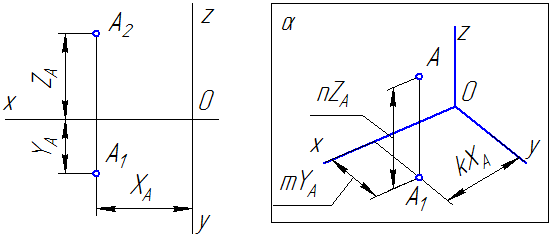
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2

Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

прямоугольные изометрические и диметрические;
косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

Видео:Прямоугольные диметрические проекцииСкачать

4.1. Прямоугольные проекции

4.1.1. Изометрическая проекция

Направление аксонометрических осей приведено на Рисунке 4.3.

Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

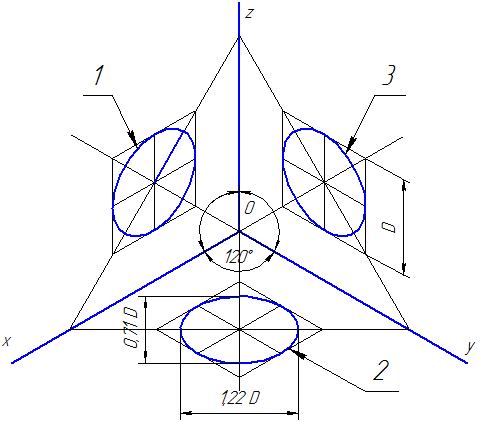
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

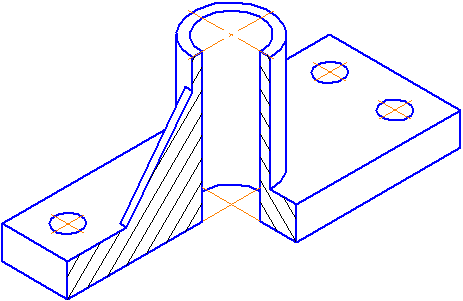
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

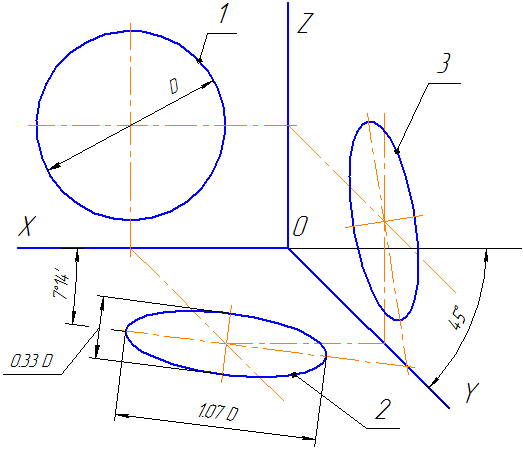
Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

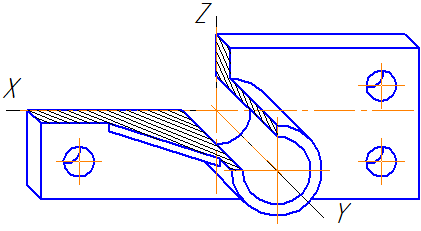
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

Видео:Аксонометрические проекцииСкачать

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

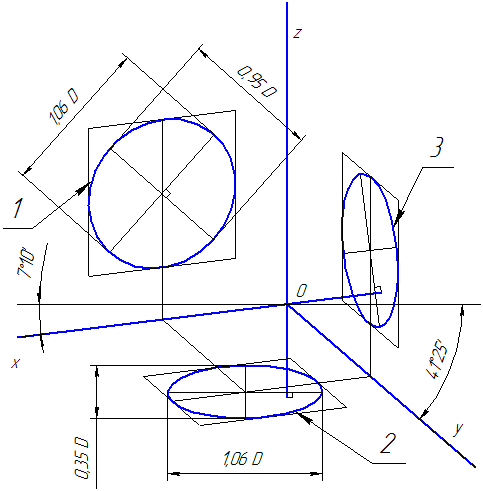
Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 30 0 и 60 0 .

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

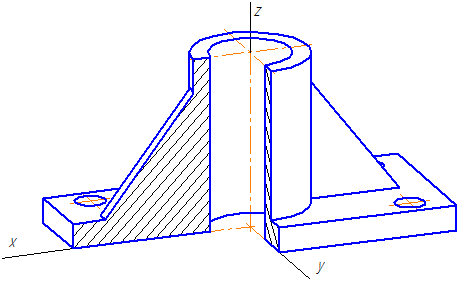
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

Видео:Косоугольная фронтальная диметрическая проекцияСкачать

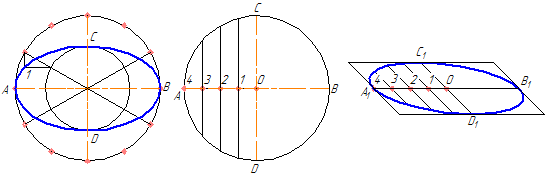
4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁ D₁ = 0,5CD. Диаметр А ₁В₁ делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

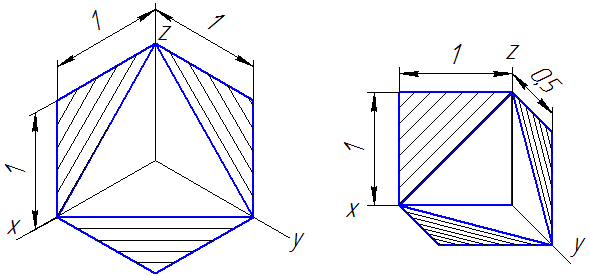
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Видео:Лекция №2. Аксонометрические проекции. Виды аксонометрии. Стандартные аксонометрические проекции.Скачать

Элементы косоугольной (фронтальной) диметрической проекции

Косоугольная (фронтальная) диметрическая проекция

Нами уже было на примерах выяснено преимущество прямоугольной (ортогональной) диметрической проекции перед изометрической. Это преимущество заключается в большей наглядности диме- трического изображения.

Основным недостатком прямоугольной диметрии является неудобное направление ее осей, затрудняющее работу по рейсшине и по треугольнику. В прямоугольной диметрии ось X отклоняется вниз от горизонтальной линии на угол в 7°, а ось Y — на угол в 41°.

Почти не потеряв в наглядности изображения, можно диметриче- ские оси значительно упростить и направить ось X горизонтально, а ось Y провести к ней под углом в 45°.

Такое положение легко получить, если систему взаимно перпендикулярных координатных осей X, Y и Z спроецировать на вертикальную (или горизонтальную) плоскость проекций не ортогонально (прямоугольно), а косоугольно, параллельным пучком лучей. Полученные в результате такого проецирования диметрические координатные оси показаны на фиг. 2 табл. 37, где попутно показан также и способ их построения. На фиг. 1 начерчен в этих осях основной диметрический куб с вписанными в его грани окружностями.

Окружность, вписанная в переднюю грань куба в косоугольных осях, не меняет формы и размеров. Это обстоятельство является одним из существенных преимуществ косоугольной проекции при вычерчивании сложных тел (например, см. табл. 39 и др.).

При вычерчивании аналогичных тел в ортогональной диметрии задача значительно усложняется необходимостью начертить большое количество эллипсов. Если в этом случае принять за основу ось косоугольной диметрии, то получим более простое решение, так как все окружности легко будет описать циркулем.

Косоугольная диметрия с большим успехом может быть применена во многих случаях практики при вычерчивании деталей со сложными контурами.

Например, на фиг. 4 табл. 38 начерчен корпус подшипника, имеющего сложное очертание формы передней стенки. В обычных ортогональных диметрических осях все криволинейные элементы этой стенки превращаются в эллипсы, чем значительно осложняется процесс вычерчивания этой детали.

На фиг. 4 табл. 38 этот подшипник начерчен в косоугольных диметрических осях, почему построение форм передней фронтальной стенки значительно упростилось. Таким образом, в косоугольной диметрии передняя фронтальная стенка изображается так же, как главный вид ортогонального чертежа. Поэтому часто в технике косоугольную диметрию называют фронтальной проекцией.

Все остальные особенности диметрии в косоугольных осях обычно сохраняются, т. е. по двум осям откладывают натуральные размеры, а по третьей оси размеры уменьшают вдвое (а иногда и в три раза).

На фиг. 4 табл. 37 начерчены цилиндры, расположенные вдоль косоугольных диметрических осей X, У, Z.

Большим недостатком верхнего и правого цилиндров является не- перпендикулярность их главных осей к координатным осям X и Z.

Такое положение осей создает непривычную для нашего глаза картину, и нам кажется, что в этих случаях начерчен не цилиндр, а косое сплющенное тело.

Однако если тот же цилиндр расположить вдоль оси У, то картина значительно меняется, и цилиндр в этом случае кажется более естественным.

Происходит это за счет сохранения перпендикулярности оси У к главной оси переднего эллипса, превратившегося в данном случае в окружность.

Так как выбор положения для главной оси при вычерчивании цилиндрических тел по большей части зависит от нашего усмотрения, то всегда целесообразно в косоугольной диметрии эти тела располагать вдоль оси У.

Преимущества косоугольной диметрии очень часто используются и для тел, имеющих прямоугольные очертания.

Например, на фиг. 3 в косоугольных диметрических осях очень эффектно могут быть представлены разного рода сложные врубки, предназначенные для соединения, положим, двух брусков в одно целое.

Косоугольная (фронтальная) диметрическая проекция

В этом случае чертим на некотором расстоянии фронтальный вид боковых стенок двух сопрягаемых брусков и затем из всех точек излома контура проводим линии, параллельные оси Y, для левого бруска отклонив их в сторону, а для правого бруска — в другую.

Отметив по этим осям размер толщины брусков, сокращенный вдвое, очень легко вычерчиваем контуры врубки; при этом форма ее выявляется с большей степенью наглядности.

На фиг. 1 показан способ определения направления главных осей для верхнего эллипса. Сделанные построения аналогичны рассмотренным выше на рис. 24 (см. параграф 1.8).

Теоретическая сторона вопроса о получении косоугольной проекции рассмотрена в части 1 настоящего пособия.

Слева вверху на фиг. 1 тонкой штрихпунктирной чертой показано построение точек эллипса, лежащих на диагоналях верхнего ромба. Для этой цели известным приемом построен прямоугольный треугольник с углами в 45° и из точки а₀ через S проведена полуокружность.

Упрощенный способ изображения окружностей в косоугольной диметрии (таблица 38)

Окружность, вписанная в грани куба, при косоугольном способе проецирования изображается эллипсами для верхней (нижней) и правой (левой) граней куба. Окружность, вписанная в переднюю грань куба, не изменяет своей формы и размеров (фиг. 1).

Вычерчивание эллипсов по точкам неудобно и отнимает много времени, поэтому и для косоугольного способа проецирования удобнее эллипсы заменить четырехцентровыми овалами, легко вычерчиваемыми при помощи кругового циркуля. Можно предложить следующий приближенный способ построения окружности в косоугольной диметрической проекции (фиг. 2).

Намечаем сначала ось эллипса. Эта ось не горизонтальна, а наклонена несколько к горизонту (см. фиг. 1 табл. 37). Можно принять наклон примерно в 7° и строить его по тангенсу, для чего, как уже знаем, можно отложить по горизонтальному направлению восемь каких- либо единиц, а по вертикальному — одну такую же единицу. Далее по намеченной оси от центра эллипса раскладываем размер диаметра окружности:

и этим намечаем большую ось эллипса. Малая ось может быть намечена перпендикулярно к большой оси, и размер малой оси составляет 1/3 от D, где D — фактический размер диаметра вычерчиваемой окружности. Здесь, как и обычно, предполагается, что сокращениями по осям X, Y и Z пренебрегаем.

Разметив большую и малую оси, приступаем к проведению очертания больших дуг овала. Для этой цели необходимо наметить положение центра ц1 и симметричного ему сверху ц1. Центр ц1 на фиг. 2 не показан. Положение центра ц1 будет определено, если вдоль малой оси эллипса от его центра отложить размер D₀.

Поставив острие циркуля в точку ц1, описываем радиусом R большую дугу овала. Радиус для малых дуг овала определяется без вычисления; этот радиус г = се. Взяв в циркуль размер хорды се, получаем величину радиуса, которым и скругляем острые концы из точек ц2 и ц2. На фиг. 3 показан способ построения четырехцентрового овала, вписанного в боковые грани куба.

Этот овал совершенно тождествен овалу, показанному на фиг. 2.

Последовательность действий при вычерчивании овала по фиг. 3 такова.

Намечаем направление большой оси овала. С этой целью по вертикальному направлению откладываем восемь и по горизонтальному направлению одну такую же единицу. На проведенной оси эллипса раскладываем диаметр вычерчиваемой окружности, увеличенный в 1,06 раза, т. е. откладываем D₀ = 1,06D, где D — фактический диаметр вычерчиваемой окружности. Перпендикулярно к большой оси намечаем направление малой оси овала и по этому направлению раскладываем размер малой оси овала:

Наметив размер большой оси овала и перпендикулярно к нему размер малой оси овала, приступаем к вычерчиванию самого овала. С этой целью определяем положение ц1 и ц2. Для нахождения ц1 откладываем от центра овала вдоль его малой оси размер D₀ и из намеченной точки ц1 радиусом R описываем большую дугу стенки эллипса.

Упрощенный способ изображения окружностей в косоугольной диметрии

Радиусом г для скругления острых концов овала является размер хорды ес, которую замеряем циркулем непосредственно по чертежу.

Необходимо запомнить, что при фронтальном способе проецирования большая ось горизонтального эллипса (см. фиг. 2) наклонена к горизонту примерно на угол 7°, а большая ось вертикального эллипса (см. фиг. 3) наклонена на такой же угол 7° к вертикальной линии. Кроме того, полезно помнить, что размер большой оси эллипса D₀

1,06D, а размер малой оси dg =—, где D — диаметр вычерчиваемой окружности. 3

На фиг. 4 показан способ изображения корпуса подшипника, вычерченного в осях косоугольной диметрии. Здесь следует обратить внимание на то, что сложные очертания фронтальной стенки и средней выемки этого корпуса могут быть легко вычерчены при помощи кругового циркуля и лишь отверстия в опорной плите проецируются в виде эллипсов, для построения которых рекомендуется сначала начертить контуры параллелограмов, в которые эти эллипсы могут быть затем вписаны либо от руки, либо при помощи циркуля, как это было показано на фиг. 2.

Составление косоугольного диметрического изображения по чертежу (таблица 39)

На фиг. 1 табл. 39 дан чертеж крышки вентиля. Крышка начерчена в двух проекциях: вид спереди (главный вид) и вид сверху для выявления внутреннего устройства детали. На главном виде сделан вырез правой четверти.

Крышка имеет круглую форму, и на проекции вида сверху (см. фиг. 1) на ней видно большое количество окружностей (отверстия, фланец и т. д.). Учитывая это обстоятельство, целесообразно крышку начертить в осях косоугольной, фронтальной, диметрии. Это и сделано на фиг. 2, где крышка поставлена в такое положение, что все ее криволинейные очертания проецируются без искажения в виде окружностей.

Для построения использованы размеры, нанесенные на фиг. 1. Последовательность построения такова: в первую очередь вычерчен большой фланец крышки и на его поверхности размечено четыре отверстия для болтов, затем начерчены верхний овальный фланец и конусовидные приливы, в последнюю очередь сделан разрез и нанесена штриховка.

Составление косоугольного диметрического изображения по чертежу