Кто ввел обозначение параллельных прямых (8 видео)

История термина параллельность. Параллельность вокруг нас.

В данной работе рассматривается термин параллельность начиная с ученых разного времени

Содержание

Просмотр содержимого документа «История термина параллельность. Параллельность вокруг нас.»
Кто ввел обозначение параллельных прямых
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Интересный факт
Историческая справка
Параллельные прямые в быту и повседневной жизни
Домашнее задание
Геометрия. 7 класс
📺 Видео

Просмотр содержимого документа
«История термина параллельность. Параллельность вокруг нас.»

Параллельность вокруг нас

Название параллельных прямых произошло от греческого слова «параллелой», которое означает «рядом идущие». Слово стало употребляться как математический термин 2500 лет назад в школе Пифагаора.

Впервые термин «параллельные прямые» возник в книге «Начала», автором которой является древнегреческий математик Евклид. Определение параллельных прямых

Евклид(3 век до н.э.), в трудах «Начала»: «Параллельные суть прямые, которые находясь в одной плоскости и будучи продолжены в обе стороны неограниченно ни с той , ни с другой стороны между собой не встречаются».

Посидоний (1 век до н.э.).

« Две прямые, лежащие в одной плоскости, равноотстоящие друг от друга».

Древнегреческий ученый Папп( вторая половина 3 века до н.э.) ввел символ параллельности прямых. Впоследствии английский экономист Рикардо (1772-1823) этот символ использовал как знак равенства. Только в 18 веке стали использовать символ.

Практические способы построения

В жизни мы часто встречаем параллельные линии, не всегда задумываясь, каким способом их получить.

Можно строить параллельные прямые с помощью имеющихся в наличии инструментов. Самый простой инструмент для построения параллельных прямых — простая линейка и угольник.

Угольник передвигаем вдоль линейки и карандашом проводим прямые, которые будут параллельны между собой.

Инструменты, используемые на практике при построении

Рейсшина – чертежный прибор для проведения параллельных линий, который состоит из линейки с поперечной планкой. Промышленность выпускает различные виды рейсшин. Здесь пример конструкторской рейсшины обычной деревянной. При помощи рейсшины можно проводить горизонтальные параллельные прямые, а при помощи рейсшины или линейки и угольника можно без труда вычерчивать и вертикальные, и наклонные параллельные прямые.

Малка — инструмент для перенесения угловых размеров при разметке деталей, для построения параллельных прямых. При выполнения столярных работ для разметки параллельных прямых используется малка (две деревянные планки ,скрепленные шарниром).

В жизни мы часто встречаемся с понятием параллельности

При строительстве зданий строго учитывается понятие параллельности. Самый наглядный пример параллельности прямых — железнодорожное полотно.

Рельсы на горизонте пересекаются, но в действительности такого быть не может. Это оптическая иллюзия.

При строительстве зданий строго учитывается понятие параллельности. Параллельные линии придают улицам особую красоту и органично вписываются в пейзаж.

Лестница задает ритм движению человека.

При сервировке стола столовые приборы раскладывают строго параллельно друг другу.

Многие животные, рыбы, насекомые имеют «параллельный» окрас.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Кто ввел обозначение параллельных прямых

Две прямые на плоскости называются параллельными, если они не пересекаются.

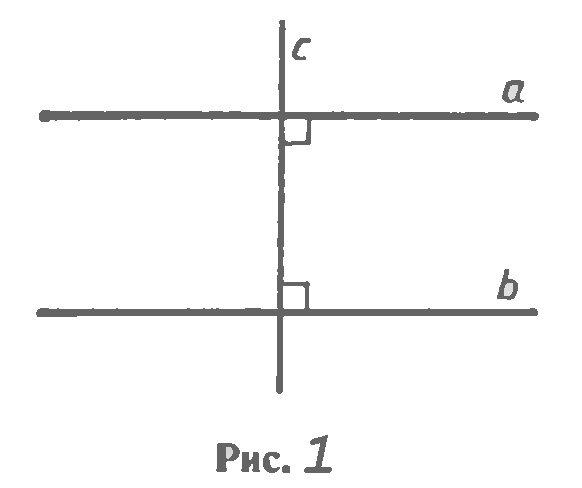
Параллельность прямых а и b обозначают так: а||b. На рисунке 1 изображены прямые a и b, перпендикулярные к прямой с. Такие прямые а и b не пересекаются, т. е. они параллельны.

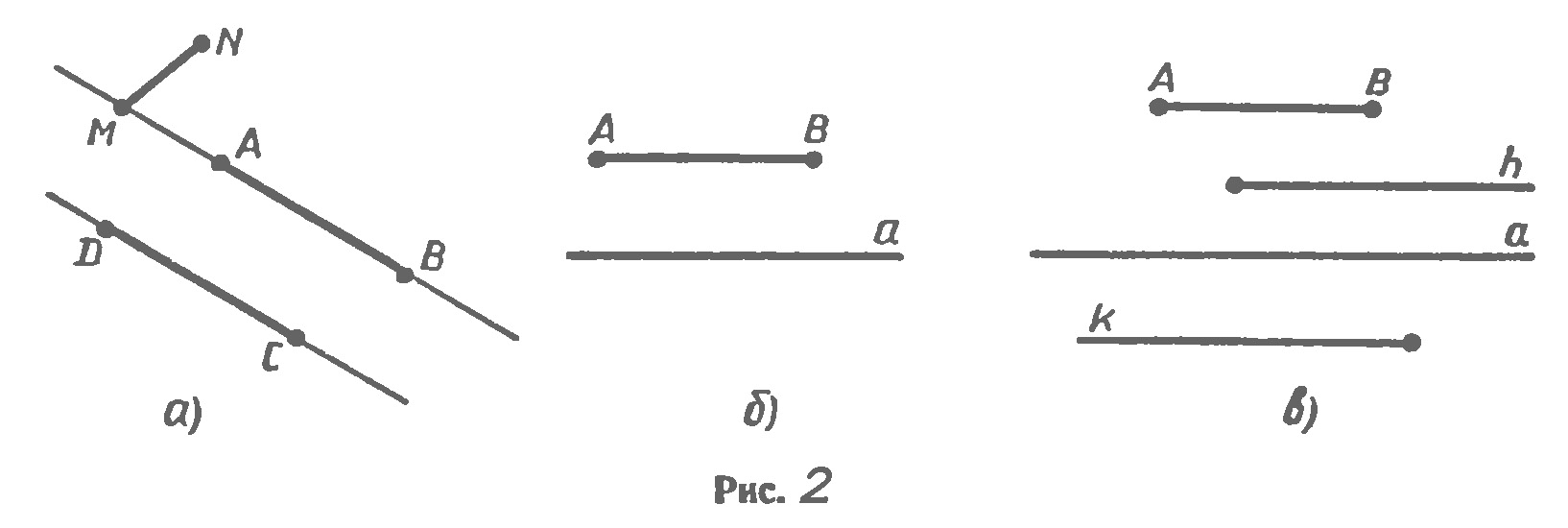
Наряду с параллельными прямыми часто рассматривают параллельные отрезки. Два отрезка называются параллельными, если они лежат на параллельных прямых. На рисунке (рис. 2,а) отрезки АВ и СD параллельны (АВ||СО) а отрезки МN и СD не параллельны. Аналогично определяется параллельность отрезка и прямой (рис. 2,б), луча и прямой, отрезка и луча, двух лучей(рис. 2,в).

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Признаки параллельности двух прямых

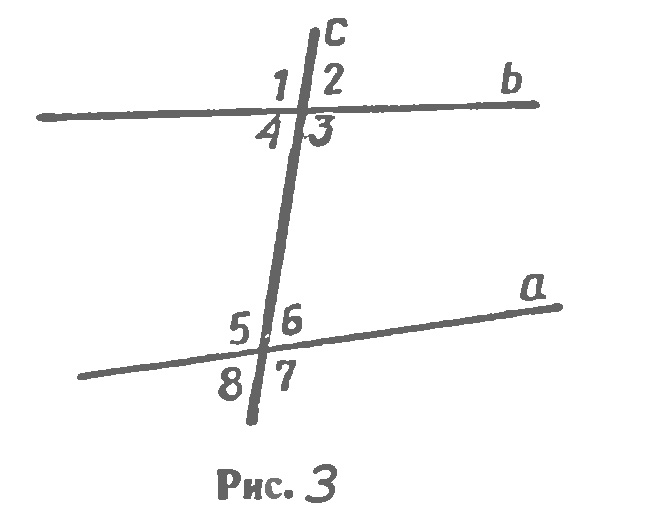
Прямая с называется секущей ми отношению к прямым а и b, если она пересекает их в двух точках (рис. 3). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 3 обозначены цифрами.

Некоторые пары этих углов имеют специальные названия:

накрест лежащие углы: 3 и 5, 4 и 6;
односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Рассмотрим три признака параллельности двух прямых, связанные с этими парами углов.

Теорема.Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

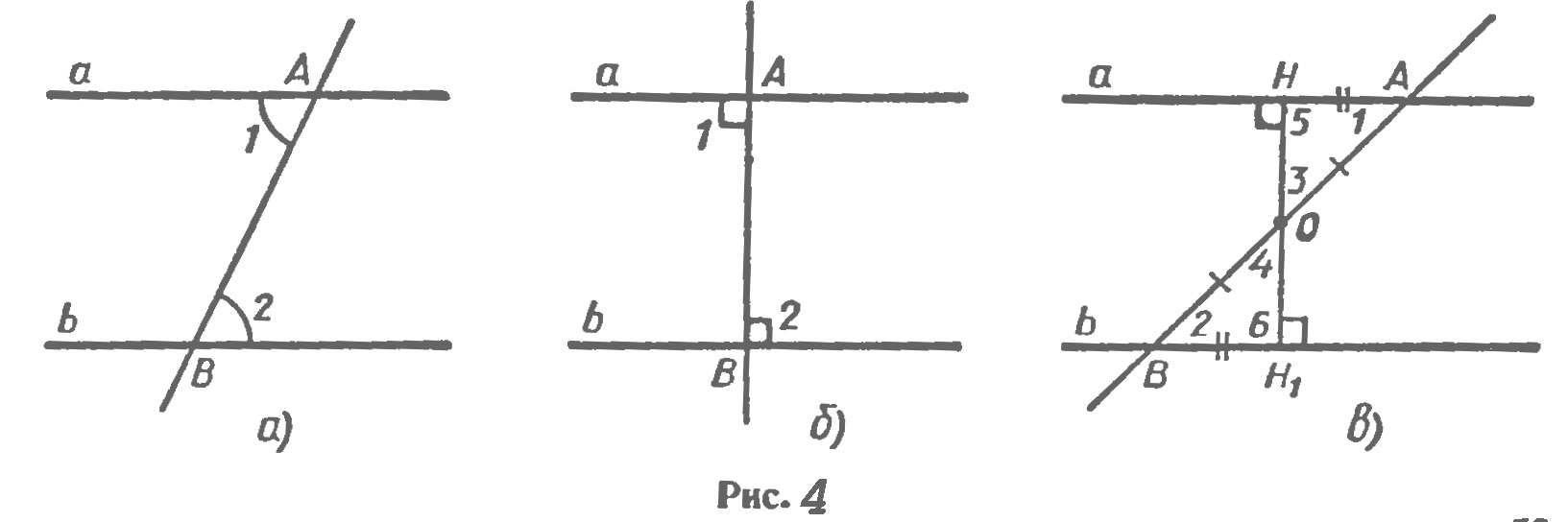
Доказательство.Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны: ∠1=∠2 (рис. 4, а).

Покажем,что а||b. Если углы 1 и 2 прямые (рис. 4, б), то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны. Рассмотрим случай, когда углы 1 и 2 не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой а (рис. 4, в). На прямой b от точки В отложим отрезок ВН1 равный отрезку AH, как показано на рисунке 4, в, и проведем отрезок ОН1. Треугольники ОНА и ОН1В равны по двум сторонам и углу между ними (АО=ВО. АН=ВН1 ∠1=∠2), поэтому ∠3=∠4 и ∠15=∠16. Из равенства ∠3=∠4 следует, что точка Н1 лежит на продолжении луча ОН, т. е. точки Н, О и Н1 лежат на одной прямой, а из равенства ∠5=∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Значит, прямые а и b перпендикулярны к прямой НН1 поэтому они параллельны. Теорема доказана.

Теорема.Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

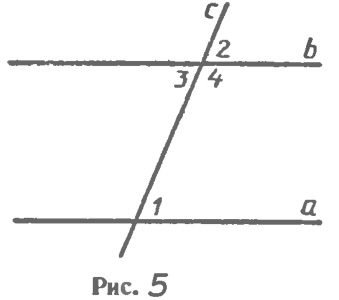
Доказательство.Пусть при пересечении прямых а и b секущей с соответственные углы равны, например ∠1= ∠ 2 (рис. 5). Так как углы 2 и 3 — вертикальные, то ∠2=∠3. Из этих двух равенств следует, что ∠1=∠3. Но углы 1 и 3 — накрест лежащие, поэтому прямые а и b параллельны. Теорема доказана.

Теорема.Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Доказательство.Пусть при пересечении прямых а и b секущей с сумма односторонних углов равна 180°, например ∠1+∠4=180° (см. рис. 5). Так как углы 3 и 4 — смежные, то ∠3+∠4=180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые а и b параллельны. Теорема доказана.

Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

Практические способы построения параллельных прямых

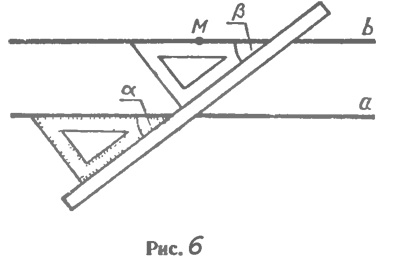
Признаки параллельности прямых лежат в основе способов построения параллельных прямых с помощью различных инструментов, используемых на практике. Рассмотрим, например, способ построения параллельных прямых с помощью чертежного угольника и линейки. Чтобы построить прямую, проходящую через точку М и параллельную данной прямой а, приложим чертежный угольник к прямой а, а к нему линейку так, как показано на рисунке 103. Затем, передвигая угольник вдоль линейки, добьемся того, чтобы точ ка М оказалась на стороне угольника, и проведем прямую b. Прямые а и b параллельны, так как соответственные углы, обозначенные на рисунке 103 буквами альфа и бета, равны.

Еще есть способ построения параллельных прямых при помощи рейсшины. Этим способом пользуются в чертежной практике.

Аналогичный способ применяется при выполнении столярных работ, где для разметки параллельных прямых используется малка (две деревянные планки, скрепленные шарниром).

Видео:7 класс, 24 урок, Определение параллельных прямыхСкачать

Интересный факт

Особое место в истории математики занимает пятый постулат Евклида (аксиома о параллельных прямых). Долгое время математики безуспешно пытались вывести пятый постулат из остальных постулатов Евклида и лишь в середине XIX века благодаря исследованиям Н. И. Лобачевского, Б. Римана и Я. Бойяи стало ясно, что пятый постулат не может быть выведен из остальных, а система аксиом, предложенная Евклидом, не единственно возможная.

Аксиома параллельных прямых

Еще древние греки придумали простой способ: как провести циркулем и линейкой через точку А, лежащую вне данной прямой l, другую прямую m, не пересекающую прямую l. Но единственно ли решение этой задачи? Или через точку А можно провести несколько разных прямых, не пересекающих исходную прямую m?

Евклид, видимо, первый среди эллинов понял, что ответ на этот вопрос нельзя получить, исходя из прочих свойств прямых и точек – тех, которые он сформулировал в виде аксиом и постулатов. Нужно ввести дополнительный постулат о единственности искомой прямой m – и назвать эту прямую параллельной!

А возможны ли иные формулировки постулата о параллельных прямых – не совместимые с постулатом Евклида? Например, можно предположить существование нескольких разных прямых, не пересекающих данную прямую l и проходящих через общую точку А. Приведет ли такое предположение к логическому противоречию или нет? Если нет, то возможны иные геометрии, кроме евклидовой!

Первую неевклидову геометрию изобрели в 1820-е годы сразу три талантливых математика: немец Карл Гаусс, русский Николай Лобачевский и венгр Янош Бойяи. Русский математик оказался самым смелым и упорным из троих открывателей. Он первый опубликовал свою книгу с предсказанием замечательных свойств неевклидовых фигур. Например, на плоскости Лобачевского сумма внутренних углов треугольника всегда меньше 180 градусов. Она принимает разные значения для разных треугольников; при этом два подобных треугольника обязательно равны!

В конце 19 века геометры Клейн и Пуанкаре изобрели довольно простые модели поверхностей, на которых воплощается геометрия Лобачевского. Еще раньше Риман заметил, что на обычной сфере воплощена третья возможная геометрия (проективная): в ней «параллельных» прямых вовсе нет, а сумма внутренних углов треугольника всегда больше, чем 180 градусов.

До начала 20 века считалось, что неевклидовы геометрии могут быть полезны только внутри математической науки. Но в 1910-е годы Эйнштейн создал Общую Теорию Относительности: она оказалась четырехмерным воплощением неевклидовой геометрии Лобачевского. С тех пор физики верят, что каждая непротиворечивая математическая конструкция воплощена где-нибудь в Природе. Возможно, что так оно и есть.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Историческая справка

В древние века, буквально 2500 лет назад, в известной школе Пифагора греческое слово «параллелос» начали употреблять, как геометрический термин, хотя определения параллельных прямых в те времена еще не знали. Но исторические факты говорят о том, что древнегреческий ученый Евклид в третьем веке до нашей эры, в своих книгах все же, раскрыл смысл такого понятия, как параллельные прямые.

Как вам уже известно, из пройденного материала в предыдущих классах, термин «параллелос» в переводе с греческого языка обозначает рядом идущий или проведенный друг возле друга.

В математике для обозначения параллельных прямых существует специальный знак. Правда, не всегда знак параллельности имел теперешний вид. Так, например, древнегреческий математик Папп в третьем веке нашей эры для обозначения параллельности пользовался знаком равно «=». И лишь в восемнадцатом веке, благодаря Уильяму Оутреду для обозначения параллельных прямых, стали использовать знак «//». Если есть, например, параллельные а и в, то на письме их следует записывать, как а//в

А вот знак «=» во всеобщее обращение ввел Рекорд и его стали использовать, как знак равенства.

Видео:7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Параллельные прямые в быту и повседневной жизни

С параллельными прямыми мы часто встречаемся в окружающей нас жизни, хотя, как правило, редко на этом акцентируем свое внимание. На уроках музыки, открывая нотную тетрадь, сразу же невооруженным взглядом мы видим линии нотного стана. Но параллельные линии вы можете увидеть не только в нотных тетрадях и сборниках песен, но и если внимательно присмотритесь к музыкальным инструментам. Ведь струны гитары, арфы или органа также расположены параллельно.

Подняв на улице глаза вверх, вы видите параллельно проходящие электрические провода. Оказавшись в метро или на железной дороге, также не сложно заметить, что рельсы расположены параллельно друг к другу.

Параллельные линии можно встретить повсюду. Они нам постоянно встречаются в быту, живописи. Без них не обойтись и в архитектуре, так как в строительстве зданий строго учитывается понятие параллельности.

Если вы внимательно посмотрите на изображение, то сразу же заметите в этих архитектурных сооружениях присутствие параллельных прямых. Возможно, они служат так долго и остаются красивыми благодаря тому, что архитекторы и инженеры при создании этих культовых зданий использовали параллельные прямые.

А задумывались ли вы когда-нибудь над тем, почему в линиях электропередач, провода располагаются параллельно? И представьте себе, чтобы было, если бы они не были бы параллельными и пересекались или соприкасались друг с другом. А это привело бы к нехорошим последствиям, при которых могло произойти замыкание, перебоям и отсутствию электричества. А что могло произойти с поездом, если бы рельсы не были бы параллельными? Об этом даже страшно подумать.

Вам всем хорошо известно, что параллельные прямые никогда не пересекаются. Но если вы долго будете смотреть вдаль, в бесконечность, то в итоге можете увидеть, как параллельные прямые пересекаются. В этом случае мы с вами столкнулись с иллюзией зрения. Может быть, только благодаря таким иллюзиям и зрительным искажениям и появилась живопись.

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Домашнее задание

1. Назовите свои примеры, где вы в повседневной жизни, в быту или в природе сталкиваетесь с моментами или фактами параллельности.
2. Какие вы знаете способы, благодаря которым можно начертить параллельные прямые? Назовите эти способы.
3. Начертите параллельные прямые в тетради, способами, которые вам известны.
4. При каких условиях прямые, можно назвать параллельными?

1. Какие прямые называются параллельными?
2. Какие практические способы построения параллельных прямых существуют.?

Видео:Параллельность прямых. 10 класс.Скачать

Геометрия. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Формулировка определения параллельных прямых.
Изображение параллельных прямых различными методами.
Как распознать на чертежах параллельные прямые?
Нахождение на рисунке пары накрест лежащих односторонних углов.

Параллельные прямые – две прямые на плоскости называются параллельными, если они не пересекаются.

Параллельные отрезки – два отрезка называются параллельными, если они лежат на параллельных прямых.

Параллельные лучи – два луча называются параллельными, если они лежат на параллельных прямых.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что на плоскости бывают пересекающиеся и непересекающиеся прямые, вы знаете, как их строить на чертеже. Теперь давайте рассмотрим прямые, которые называются параллельными, и научимся их строить различными способами.

Для начала дадим определение параллельным прямым.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Параллельные прямые имеют своё обозначение: a ║ b.

Рассмотрим прямые а и b, перпендикулярные прямой c. Ранее мы выяснили, что такие прямые не пересекаются, следовательно, прямые а и b параллельны.

Очень часто рассматриваются не только параллельные прямые, но и параллельные отрезки.

Дадим им определение.

Два отрезка называются параллельными, если они лежат на параллельных прямых.

Два луча называются параллельными, если они лежат на параллельных прямых.

Рассмотрим прямую с, пересекающую прямые а и b.

Прямая c называется секущей по отношению к прямым a и b, если она пересекает каждую из них.

Как видно из рисунка, при пересечении прямых а и b секущей c образуются 8 углов. Пронумеруем полученные углы.

Оказывается, некоторые пары образованных углов имеют свои названия.

Так, например, углы 3 и 5, 4 и 6 ‑ называются накрест лежащие углы.

Углы 4 и 5 или 3 и 6 ‑ называются односторонними углами.

А пары углов 1 и 5, 4 и 8, 2 и 6 или 3 и 7 ‑ называются соответственными углами.

Как же можно построить параллельные прямые?

Для построения параллельных прямых существует несколько способов построения с помощью различных чертёжных инструментов. Рассмотрим построение параллельных прямых с помощью чертёжного угольника и линейки.

Построим прямую b, проходящую через точку M и параллельную данной прямой а.

Приложим чертёжный угольник к прямой а, к нему приложим линейку. Теперь передвинем угольник вдоль линейки так, чтобы точка M оказалась на стороне угольника, остается провести прямую b. Прямые а и b будут параллельны, на основе признаков параллельности двух прямых, которые будут изучены позднее.

Материал для углублённого изучения темы

Другие способы построения параллельных прямых.

Рассмотрим ещё два способа построения параллельных прямых с помощью чертёжных инструментов.

В чертёжной практике очень часто используется способ построения параллельных прямых с помощью рейсшины.

При выполнении столярных работ, для разметки параллельных прямых используется ещё один инструмент – малка, который представляет собой две планки, скреплённые шарниром.

При нанесении параллельных рисок можно использовать рейсмус, который представляет собой деревянную заготовку с двумя регулируемыми брусками, на концах который прикреплены для нанесения рисок иглы или гвозди.

Разбор заданий тренировочного модуля

№ 1. Один из односторонних углов при двух параллельных прямых и секущей на 40º меньше другого. Найдите меньший угол, если известно, что сумма односторонних углов равна 180°.

Пусть х – меньший из односторонних углов, тогда больший равен х + 40. Т. к. сумма односторонних углов по условию равна 180°, составим уравнение.

х = 70° – градусная мера меньшего угла.

№ 2. Через параллельные прямые а и m проведены секущие АК и КР так, как показано на рисунке. КО = ВК = АК, при этом АК = КР = 9 см, отрезок ВО =АР, АР = 6 см. На сколько сантиметров периметр ∆ВОК меньше периметра ∆АКР?