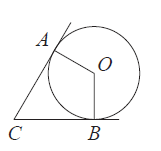Угол с равен 68 градусов вписана окружность

В угол С равен угловой величине 68° вписана окружность, которая касается сторон угла в точках А и В. Найдите угол ∠АОВ.

Угол A и B прямые, так как ОA и OB радиусы проведенные к касательным.
СО — биссектриса, так как равноудалена от сторон угла.

∠OCB = 68°:2=34°
Найдем угол ∠COB из прямоугольного треугольника ∆COB
(сумма углов в треугольнике равна 180 градусам):
180°-34°-90°=56°

Найдем угол ∠AOB:
∠AOB=2∠COB
2•56=112° градусов

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

В угол $C$, равный $68^$.

Задание:

Решение:

Первое решение:

Радиус окружности перпендикулярен касательной в точке касания, поэтому углы $CAO$ и $CBO$ прямые, т.е. по $90^$. В четырехугольнике $AOBC$ сумма углов равна $360^$, значит, угол $AOB$ будет равен $360^-90^-90^-83^=112^$.

Второе решение:
Углы $CAO$ и $CBO$ прямые, так как $OA$ и $OB$ радиусы проведенные к касательным. $CO$ — биссектриса, так как равноудалена от сторон угла, а биссектриса делит угол пополам, это значит, что угол $OCB$ равен $68^div 2=34^$.

Найдем угол $COB$ из прямоугольного треугольника $COB$, при этом мы знаем, что сумма углов в треугольнике равна $180^$: $180^-34^-90^=56^$. А ранее мы писали, что биссектриса делит угол пополам, значит, угол $AOB$ будет равен $56^cdot 2=112^$.

Угол с 68 градусов в окружность

В угол С равен угловой величине

В угол С равен угловой величине 68° вписана окружность, которая касается сторон угла в точках А и В. Найдите угол ∠АОВ.

Угол A и B прямые, так как ОA и OB радиусы проведенные к касательным.
СО — биссектриса, так как равноудалена от сторон угла.

∠OCB = 68°:2=34°
Найдем угол ∠COB из прямоугольного треугольника ∆COB
(сумма углов в треугольнике равна 180 градусам):
180°-34°-90°=56°

Найдем угол ∠AOB:
∠AOB=2∠COB
2•56=112° градусов

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

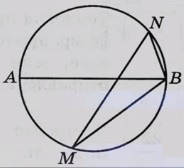
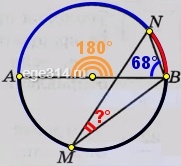
Решение №2117 На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что ∠NBA = 68°. Найдите угол NMB.

На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что ∠NBA = 68°. Найдите угол NMB. Ответ дайте в градусах.

Источник: ОГЭ Ященко 2022 (36 вар)

AB – диаметр, делит окружность на две равные части по:

360°/2 = 180°

Заметим, что дуги на которые опираются ∠NBA и ∠NMB в сумме дают 180°:

‿AN + ‿NB = 180°

Дуга ‿AN в два раза больше угла который на неё опирается:

‿AN = 2·∠NBA = 2·68º = 136°

136° + ‿NB = 180°
‿NB = 180° – 136° = 44°

∠NMB равен половине дуги ‿NB на которую опирается:

∠NMB = ‿NB/2 = 44°/2 = 22°

Углы, связанные с окружностью

Вписанные и центральные углы

Углы, образованные хордами, касательными и секущими

Доказательства теорем об углах, связанных с окружностью

Вписанные и центральные углы

Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.

Теоремы о вписанных и центральных углах

Фигура	Рисунок	Теорема
Вписанный угол

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанный уголВписанные углы, опирающиеся на одну и ту же дугу равны.Вписанный уголВписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хордыВписанный уголДва вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хордыВписанный уголВписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметрОкружность, описанная около прямоугольного треугольника

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Теоремы об углах, образованных хордами, касательными и секущими

Вписанный угол

Окружность, описанная около прямоугольного треугольника

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Угол, образованный секущими, которые пересекаются вне круга

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Угол, образованный касательной и хордой, проходящей через точку касания

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Угол, образованный касательной и секущей

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Угол, образованный двумя касательными к окружности

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство

Угол, образованный пересекающимися хордами хордами

Формула:

Угол, образованный секущими секущими , которые пересекаются вне круга

Формула:

Угол, образованный касательной и хордой хордой , проходящей через точку касания

Формула:

Угол, образованный касательной и секущей касательной и секущей

Формула:

Угол, образованный двумя касательными касательными к окружности

Формулы: