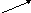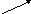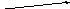Урок по математики векторы

Конспект урока по геометрии по теме: «Понятие вектора. Действия над векторами».

Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Скачать:

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Предварительный просмотр:

Тема: Понятие вектора. Действия над векторами.

• Ввести определения вектора в пространстве, равенства векторов. Рассмотреть правила действия над векторами, правило сложения нескольких векторов в пространстве.
• Воспитывать личностные качества обучающихся (умение слушать), доброжелательность по отношению к окружающим, внимательность, аккуратность, дисциплинированность.
• Развивать пространственное воображение и логическое мышление обучающихся, умение быстро ориентироваться в обстановке; развивать сообразительность, находчивость, тренировать память.

2. Мотивация урока.

Поразмышляйте над содержанием пословицы

«Плохо, когда сила живет без ума, да нехорошо, когда и ум без силы». То есть, если есть сила, то надо знать, куда ее направить. От этого зависит, будет ли пружина сжиматься или растягиваться, полетит ли мяч в ворота противника или в собственные и многое другое. Вы уже, конечно, догадались, что сегодня речь пойдет о векторах, причем о векторах в пространстве. Геометрия – одна из самых интереснейших наук, которая изучает много важных и интересных тем. Одна из них – это “Векторы”. С понятием “Вектор” вы уже знакомы, но вы знакомы с векторами на плоскости, а сегодня мы пополним свои знания о векторах и рассмотрим “Векторы в пространстве”

3. Актуализация опорных знаний.

1. Что называется вектором на плоскости?
2. Приведите пример векторных величин.
3. Что такое абсолютная величина вектора; направление вектора?
4. Какие векторы называются равными?
5. Сформулируйте правила сложения двух векторов на плоскости.
6. Какой вектор называют разницей двух векторов?

4. Объяснение нового материала сопровождается презентацией:.

Векторы на плоскости были изучены в 9 классе в разделе “Планиметрия”. Сегодня на уроке рассмотрим векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия сходны с определением вектора на плоскости и связанными с ним понятиями.

Раз мы уже знакомы с векторами на плоскости, то нам будет не трудно говорить о векторах в пространстве. Результатом нашей работы станет опорный конспект.

Что такое вектор? Как построить вектор? Как обозначаются вектора?

Обратите внимание: что над буквенным обозначением вектора ставится стрелка или черта- в разной литературе по- разному. Так, например, в учебнике физики — стрелка, а в учебнике геометрии — черта.

Вектором называется направленный отрезок.

Вектор характеризуется следующими элементами:
1) начальной точкой (точкой приложения);
2 )направлением;
3) длиной («модулем вектора»).

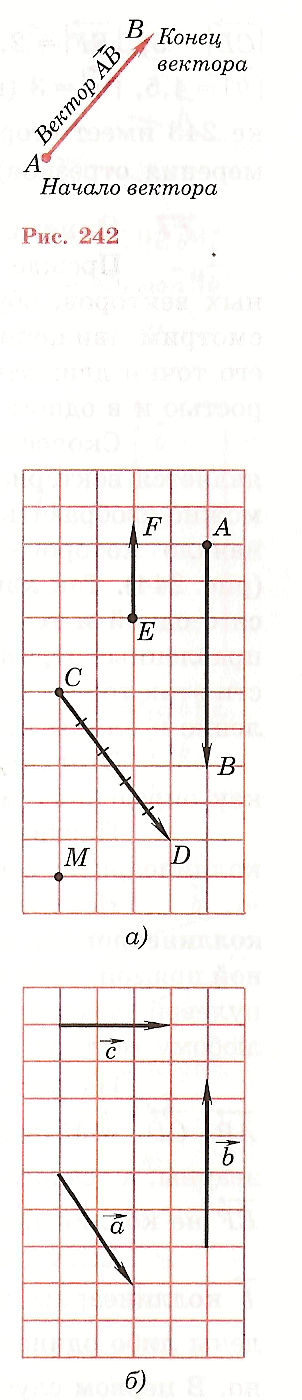
Если начало вектора — точка А, а его конец — точка В, то вектор обозначается или .

От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.

Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления. Обозначается: .

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора . Обозначается .

Два вектора называются равными , если они совмещаются параллельным переносом.

Два ненулевых вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.
Если векторы и коллинеарны и их лучи одинаково направлены, то векторы и называются сонаправленными . Обозначаются .
Если векторы и коллинеарны, а их лучи не являются сонаправленными, то векторы и называются противоположно направленными .
Обозначаются . Нулевой вектор условились считать сонаправленным с любым вектором.

Свойство коллинеарных векторов

Если векторы и коллинеарны и , то существует число k такое, что . причем если k > 0, то векторы и сонаправленные, если k

Правило треугольника . Каковы бы ни были точки А, В, С, имеет место векторное равенство:

Правило параллелограмма . Если векторы и неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм. Диагональ параллелограмма есть сумма двух векторов и .

Координаты вектора. Числа x, y и z называются координатами вектора в данном базисе. В этом случае пишут:

Действия над векторами, заданными своими координатами

При сложении векторов их соответстветственные координаты
складываются.

При вычитании векторов их соответстветственные координаты
вычитаются.

При умножении вектора на число все его координаты умножаются на это число.

1. Запишите координаты вектора АО, если А(6;-2;4), О – начало координат?
2. Найти координаты вектора АВ, если А(3; 4; -1) и В( -2; 0; 4)
3. Дано: АВ= СD, где А ( 1;0;1),В ( -1; 1;2), С (0;2;-1). Найти: D( х ,у,z)

Коллективное решение задач:

1. В пространстве даны точки А, В, С, D. Найдите вектор с началом и концом в этих точках, который равен: а) ВС+СА+АD; б) АВ+ВD+BA-CD.
2. Найдите координаты конца вектора АВ(1;-3;7), если А(2;5;-1).
3. У какого из приведенных векторов самая большая длина:

6. Зарядка для глаз.

1. Что называют вектором?
2. Выполняется ли правило параллелограмма и правило треугольника в случае сложения векторов в пространстве?
3. Сформулируйте правило параллелепипеда для сложения векторов в пространстве?
4. Какие векторы называются равными?
5. Какие векторы называются сонаправленными в пространстве; противоположно направленными в пространстве?

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

По теме: методические разработки, презентации и конспекты

Уроки геометрии по теме «Вектор. Действия с векторами»

Уроки с использованием КМ-школы.

презентация «Векторы.Действия над векторами.Проекция вектора»

В 10 классе при рассмотрении основ кинематики возникает необходимость работы учащимся с векторными величинами. Данная презентация может быть использована для повторения математических основ поня.

«Координаты вектора. Действия над векторами, заданными координатами. Построение векторов с помощью программы GeoGebra»

Разработка урока геометрии в 9 классе с помощью программы GeoGebra.

9 класс. Вектора. Действия над векторами

Презентация для учащихся 9-х классов по теме вектора.

Конспект урока по математике на тему «Понятие смешанной дроби»

Данный урок предназначен для учащихся 5 класса.Содержание учебного материала соответствует цели урока, требованиям учебной программы и стандарту образования. На уроке используются различные формы орга.

План-конспект урока и презентация по теме: «Понятие о наречии» (русский язык, 7 класс).

Данный урок проводится по методическому комплексу М.М. Разумовской.

Методическая разработка урока: «Векторы в пространстве. Действия с векторами. Скалярное произведение векторов»

Методическая разработка урока обобщения и систематизации знаний с использованием эвристического метода обучения и компьютерных технологий.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Конспект открытого урока «Векторы. Действия над векторами»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Не пропустите открытие тысячелетия! // Vital MathСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Данный урок является вторым в разделе «Векторы».

Теме «Векторы в пространстве» в примерной программе ФИРО отводится 12 часов.

Темы разбиты следующим образом:

Понятие вектора. Действия над векторами

1.Скалярные и векторные величины. Угол между векторами. Сумма векторов

2.Противоположные векторы. Разность векторов. Умножение вектора на число

3.Коллинеарные векторы. Разложение вектора

Прямоугольная декартова система координат

4.Прямоугольная декартова система координат. Координаты вектора. Длина вектора

5.Скалярное произведение векторов. Свойства скалярного произведения

6.Угол между векторами

Для гуманитарного и естественно-научного профилей профессионального образования более характерным является усиление общекультурной составляющей учебной дисциплины с ориентацией на визуально-образный и логический стили учебной работы.

Урок проводится в нестандартной форме с целью поддержания интереса к предмету. Учащиеся на подобных уроках получают хороший эмоциональный заряд, так как урок проходит в непринужденной доброжелательной обстановке. Важным положительным эффектом применения компьютерной техники на уроке является повышение мотивации учения. При изучении темы “Векторы в пространстве” необходимо актуализировать довольно большой объем знаний, полученных в 9 классе. С использованием компьютера этот процесс идет значительно быстрее, а за счет экономии времени удается рассмотреть большее количество задач, сократить время на повторение пройденного материала и усвоение нового материала за счет большей наглядности и активизации зрительной памяти. Чертеж, выполненный на доске, проигрывает виртуальному уже хотя бы потому, что виртуальный можно воспроизводить в неизменном виде (что актуально для зрительной памяти) любое количество раз; при необходимости можно возвращаться к предыдущим этапам построения.

Использование компьютерных технологий в образовательном процессе вообще и на уроках математики в частности, позволяет придти к следующим выводам:

Мультимедийная система обеспечивает :

· Наглядность материала, в том числе, за счет звука, цвета, движения;

· Ускорение темпа урока;

· Свободу постоянного экспериментирования с целью улучшения методики преподавания;

· Последовательный характер обучения за счет планомерного накапливания наглядных электронных пособий, позволяющих с легкостью в любой момент вернуться к уже знакомым, эмоционально окрашенным образам пройденного материала, которые могут быть гораздо экспрессивнее всем известных опорных сигналов.

Компьютер на уроке — это педагогическая реальность, которая твердо вошла в нашу жизнь; при этом компьютер можно рассматривать как еще одно дополнение к процессу обучения, а не заменяющее учителя и учебник средство обучения.

В этой теме основной акцент делается на формирование наглядных представлений. Для каждого из рассматриваемых случаев даются определения и некоторые признаки. При изучении определений и свойств векторов основное внимание необходимо уделить усвоению формулировок и умению применять их к решению задач.

Основное внимание направлено на задачи вычисления суммы и разности векторов, нахождения координат вектора, через начало и конец вектора , умножения вектора на число, а также признака коллинеарности векторов. При повторении определений равных и сонаправленых, противоположных и противоположнонаправленных векторов особое внимание следует уделить “реальному” изображению этих векторов. С этой целью различные векторы иллюстрирую на отдельных слайдах и на прямоугольном параллелепипеде.

Работая на уроке, учащиеся овладевают:

1. Учебно-интеллектуальными умениями и навыками:

— по формулам вычисляют координаты вектора, длину вектора, сумму и разность векторов, умножают вектор на число.

— анализируют учебный материал 9 класса , сравнивают коллинеарные векторы, равные, сонаправленные, противоположные и противоположнонаправленные векторы по их координатам и представляя их графически.

— планируют работу, осуществляют самоконтроль.

Чтобы урок для учащихся был активным и максимально индивидуализированным, чтобы реализовались особенности каждого учащегося, применяю технологию интерактивного обучения с опорными конспектами.

Тема урока: Векторы в пространстве. Действия с векторами

· Ввести понятие вектора в пространстве, его длины, понятие коллинеарных и равных векторов; действия над векторами в пространстве.

· Развитие пространственного воображения учащихся.

· Развивать умения строить логическую цепочку рассуждений, анализировать, выделять главное, сравнивать, строить аналогии , обобщать и систематизировать, делать выводы.

· Развивать умение работать в должном темпе.

· Воспитание умения слушать, умения работать в малых группах.

· Воспитание познавательного интереса к предмету.

· Активизация мыслительно-познавательной деятельности учащихся.

· Создание условий для формирования знаний, умений и навыков

Тип урока: урок изучения нового материала.

Вид урока: урок с компьютерным сопровождением.

Интерактивная технология: работа с опорным конспектом, во время компьютерного сопровождения

Учебный предмет: геометрия

Уровень образования школьников: урок проводился с учащимися 1 курса колледжа «Подмосковье».

Метод обучения : наглядный; демонстрация мультимедийной презентации.

· опорные конспекты “Векторы на плоскости и в пространстве”.

Алгебра: «Действия над действительными числами»

Физика: «Сила», «Скорость», «Движение», «Давление»

А так же биология, химия, экономика, психология, литература

I. Организационный момент.

II. Мотивация учебной деятельности.

III. Изучение нового материала и применение знаний при решении типовых задач.

IV. Самостоятельное применение знаний, умений и навыков.

V. Задание на дом.

I. Организационный момент.

Преподаватель приветствует учащихся и отмечает в журнале отсутствующих.

II . Мотивация учебной деятельности .

Вступительное слово преподавателя:

Эпиграфом к нашему уроку я взяла высказывание американского физика Юджина Пола Вигнера: “Математика — это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями“. Сегодня как раз мы и будем заниматься такими хитроумными операциями над специально разработанными понятиями.

Мой первый слог — почтенный срок,

Коль прожит он недаром;

Модель второго на столе,

Румяна, с пылу с жару.

Меня вы встретите везде –

Такой я вездесущий.

А имя громкое мое –

Преподаватель сообщает тему урока и ставит задачу совместного сотрудничества с учащимися на период урока,

В наши дни понятие «вектор» постоянно встречается в газетных и журнальных пуб­ликациях, в выступлениях политиков, уче­ных, педагогов. Обсуждая важнейшие про­цессы в жизни общества, говорят о векторе реформ и его социальной составляющей, о векторе экономических преобразований и его изменении, о направлении вектора раз­вития системы образования.

С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор.

Понятие о век­торе как направленном отрезке вошло в сознание и речь современного образованно­го человека.

Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831).

А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу

Гибсс — американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.

Образ Гиббса запечатлён в «Галерее славы великих американцев». Его имя присвоено многим величинам и понятиям химической термодинамики: энергия Гиббса, парадокс Гиббса, правило фаз Гиббса, уравнения Гиббса — Гельмгольца, уравнения Гиббса — Дюгема, лемма Гиббса, треугольник Гиббса — Розебома и др.

Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа.

Почти одновременно с ним исследованиями в том же направлении занимался

английский математик — Уильям Кингдон Клиффорд (1845–1879)

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.

Предлагается учащимся сделать небольшие выступления по заданной теме

Вектор используются везде, даже там, где мы их не замечаем, например в литературе:

Маргарита Алигер, биография которой вызывает искренний интерес у поклонников ее творчества, – знаменитая советская поэтесса, удостоившаяся Сталинской премии второй степени за поэму «Зоя» о бесстрашном подвиге советской девушки Зои Космодемьянской. После семилетки училась в химическом техникуме. С детства писала стихи.

Векторы в физике.

О, физика, наука из наук!
Все впереди!
Как мало за плечами!
Пусть химия нам будет вместо рук,
Пусть станет математика очами.
Не разлучайте этих трех сестер,
Познания всего в подлунном мире.
Тогда лишь будет ум и глаз остер,
И знанье человеческое шире.

Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу равна нулю. А сила, как известно, векторная величина.

В химии. Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца. Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее, основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».

Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы. Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.

Векторы в экономике

Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора. Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.

Векторы в психологии

На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов. Системно-векторная психология позиционируется не как отрасль классической психологии или определенное течение, а как отдельная наука изучения типологии личности.

Вектор – это симбиоз физиологических и психологических качеств человека. Это — характер, темперамент, здоровье, привычки индивида.

Векторы в повседневной жизни

Мы обратили внимание, что векторы, помимо точных наук, встречаются нам каждый день, т.е. повседневно. Векторы – указатели, которые помогают нам быстро найти тот или иной объект, отдел и сэкономить время, или стрелки дорожных знаков.

В курсе 9 класса вы изучали векторы на плоскости

Перед нами стоит задача – дать определение вектора в пространстве, научиться находить его длину по координатам начала и конца вектора и рассмотреть основные действия над векторами: сложение, вычитание, умножение на число, а также рассмотреть коллинеарные и компланарные векторы.

Поставленную перед нами задачу мы будем решать на основе сравнительного анализа и установления закономерностей: как давались определения вектора и операций над векторами на плоскости и как они формулируются для векторов в пространстве. На каждой парте лежат опорные конспекты, правую часть которых необходимо заполнить учащимся, пользуясь материалом учебника.

III . Изучение нового материала и применение знаний при решении типовых задач.

На прошлом уроке вы составляли опорные конспекты. где отмечали основные определения и действия с векторами на плоскости. Теперь я предлагаю вам в этих же конспектах заполнить вторую часть их

Определение. Вектором называется направленный отрезок

Длина этого отрезка называется длиной (модулем, абсолютной величиной) вектора.

=

| | = АВ

(х₂ – х₁; у₂ – у₁)

(________;_________;__________)

Длина вектора. (х; у)

= + у 2

Длина вектора. (х; у; z )

= √

Векторы .лежащие на одной прямой или на парраллельных прямых

Признак коллинеарности векторов

(х₁; у₁) ( x ₂ ; y ₂ )

=

Признак коллинеарности векторов

(х₁; у₁; z ₁ ) ( x ₂ ; y ₂ ; z ₂ )

Равные векторы. У равных векторов равны соответствующие координаты.

(х₁; у₁) х₁ = х₂

(х₂; у₂) у₁ = у₂

Векторы равны, если:

1. Равны длины векторов

2. Векторы сонаправлены

(х₁; у₁; z ₁ )

( х₂; у₂; z ₂ )

Векторы равны, если:

(х₁; у₁) x ₁ = — x ₂

( x ₂ ; y ₂ ) y ₁ = — y ₂

(х₁; у₁; z ₁ )

( x ₂ ; y ₂ ; z ₂ )

(х₁; у₁) и ( x ₂ ; y ₂ )

+ = ( x ₁ + y ₁ ; x ₂ + y ₂ )

Сумма векторов (х₁; у₁; z ₁ ) и ( x ₂ ; y ₂ ; z ₂ )

+ = (______; ______;_______)

Разность векторов

(х₁; у₁) и ( x ₂ ; y ₂ )

— = ( x ₁ — y ₁ ; x ₂ — y ₂ )

Разность векторов (х₁; у₁; z ₁ ) и ( x ₂ ; y ₂ ; z ₂ )

— = (______; _______;________)

Умножение вектора на число

Умножение вектора на число

λ (х; у; z ) = (λх; λу; λ z )

Дайте определение вектора в пространстве и запишите его в таблицу.

Как найти координаты вектора, зная координаты точек начала и конца вектора., запишите в таблицу

Задача Найдите координаты вектора , если М(10; -4; 2) и К(16; 2 -5).

Как вычислить длину вектора, зная его координаты, запишите в таблицу

Задача 2. Найдите модуль вектора ( — 5; 1; 2).

Ответ:

Любая точка пространства является нулевым вектором. Длина нулевого вектора равна 0.

Коллинеарные вектора , сонаправленные, противоположнонаправленные, признак коллинеарности , записать в таблицу

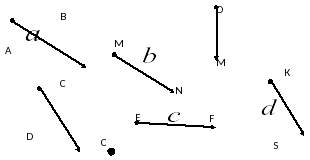
Устно решить задачу. Какие векторы на рисунке сонаправлены, противоположнонаправлены. Найти длины векторов

Равенство векторов, противоположные векторы, записать в таблицу

Могут быть ли равными векторы?

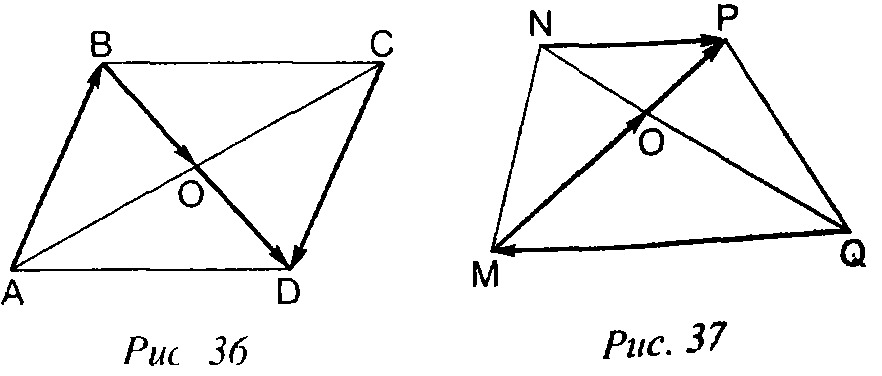
Сколько равных векторов изображено на рисунках?

При каком значении n векторы (4; 2 n — 1; -1) и (4; 9 – 3 n ; -1) равны?

Дайте определение суммы векторов. А если сложить несколько векторов в пространстве, какая фигура получится?

Заметили ли вы, что многоугольник, который получается при построении суммы нескольких векторов, может оказаться пространственным, т. е. не все его вершины лежат в одной плоскости?

Задача 5 . Найдите сумму векторов и , если А(2; 3; -1), С(3; -2; 0), а В – произвольная точка пространства

Ответ: (1; -5; 1)

Дайте определение разности векторов.,запишите в таблицу

Задача 6. Найдите разность векторов и , если В(3; 7; 10), С(1; 9; -6), а А – произвольная точка пространства.

Ответ: (2; -2; 16)

Как умножается вектор на число?,запишите в таблицу

Задача 7. Найдите координаты вектора с = 2а -3 b , если а(7; -3; 0) и b (4; 1; -2)

Задача 8 . Найдите абсолютную величину вектора 3 , если (4; -4; 2) Рассмотреть 2 способа решения.

Ответ: = 18

IV. Самостоятельное применение знаний, умений и навыков.

1.Что называется вектором?

б)отрезок, обозначенный двумя заглавными латинскими буквами

в) отрезок с выбранным направлением

2. Какой вектор является нулевым?

а)длина вектора равна 0

б)вектор лежит на прямой

в)вектор обозначен одной буквой

3. Векторы коллинеарны, если…

а)лежат на прямых

б)лежат на параллельных прямых

в)один из векторов нулевой

5. Векторы называются равными, если …

а)их длины равны

б)их модули равны и векторы направлены в одну сторону

в)они отложены от одной точки

Даны векторы (-3; 0; 4) и (2; 4; -4)

1. Длину вектора .

2. При каких значениях k и m вектор ( k ; -3; m ) коллинеарен вектору ?

3. Из векторов (1; 1; -2), (-1; -2; 2), (2; -4; 4), (-4; -4; 2) укажите векторы противоположнонаправленные с вектором .

Дано:

1) Находим координаты вектора

;

2) Затем находим координаты вектора

3) Теперь находим аналогично координаты вектора

4) Теперь находим сумму данных векторов, складывая соответствующие координаты:

Ответ:

С учетом познавательных и когнитивных способностей необходимо учащимся раздать разноуровневые задания на применение навыков и умений действий над векторами (работа в тетрадях).

1. Найдите координаты вектора , если

2. Даны векторы и Найдите координаты и длину вектора .

1. Даны векторы и Найдите координаты и длину вектора .

2. Даны векторы Найдите координаты вектора

3. Найдите длину вектора , если

1. Даны векторы Найдите координаты вектора

2. Найдите длину вектора , если

3. Из точки построен вектор . Найдите координаты точки , если:

4. Даны векторы и Найдите координаты и длину вектора .

Данный вид работы учащиеся выполняют в тетрадях, после чего учитель собирает тетради для проверки.

V . Задание на дом. (слайд 54)

Закончи предложение: Я умею …, я могу …, я знаю ….

VII . Итог урока. Оценивание учащихся.

Видео:Вычитание векторов. 9 класс.Скачать

«Векторы»

ввести определение вектора, нулевого вектора, длины вектора, коллинеарных векторов, равных векторов, сонаправленных и противоположно направленных векторов,

— развитие навыков выполнения рисунков; правильности обозначения векторов;

— воспитывать внимательность и аккуратность при обозначении и построении

векторов, взаимопомощь при изучении темы.

Просмотр содержимого документа
«»Векторы»»

Тема: «Понятие вектора. Модуль и направление вектора. Равные вектора».

Цель: — ввести определение вектора, нулевого вектора, длины вектора, коллинеарных векторов, равных векторов, сонаправленных и противоположно направленных векторов,

— развитие навыков выполнения рисунков; правильности обозначения векторов;

— воспитывать внимательность и аккуратность при обозначении и построении

векторов, взаимопомощь при изучении темы.

1. Организационный момент

«Образование – это не количество прослушанных уроков, а количество понятых. Так что, если хотите идти вперед, то поспешайте медленно и будьте внимательны»

2. Мотивация урока.

Мой первый слог — почтенный срок,

Коль прожит он недаром;

Модель второго на столе,

Румяна, с пылу с жару. (Век-тор)

Группа туристов вышла в трехдневный поход. На туристической базе было известно, что за день группа проходит 30 км. На следующий день группа связалась по рации с турбазой и только успела передать, что один из туристов повредил ногу и не может двигаться дальше, как связь прервалась. Что предпринять руководителю туристической базы? Что необходимо знать, чтобы как можно скорее прийти на помощь группе?

Спасибо за ваши предложения. Сегодня мы узнаем ответы на этот и многие другие вопросы, связанные с определением положения тела в произвольный момент времени. Мы ближе познакомимся с понятием вектора, перемещения, научимся изображать векторы, определять их направление.

3. Актуализация опорных знаний.

-скалярные величины (имеют числовое значение): масса, площадь, длина, объём, время, температура.

— векторные величины (имеют числовое значение и направление): сила, перемещение, скорость, ускорение, вес.

4. Изучение нового материала.

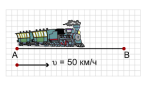
Многие величины полностью характеризуются своими численными: длина, площадь, температура, цена. Их называют скалярными величинами или скалярами. Но есть и такие величины, которые характеризуются не только своим численным значением, но и направлением: сила, скорость, перемещение. Например, мало знать, что скорость поезда равна 50 км/ ч. Надо знать еще в каком направлении движется этот поезд. Указать направление можно, например, стрелкой.

Так, поезд движется со скоростью 50 км/ч из пункта А в пункт В. Величины, которые характеризуются не только своими числовыми значениями, но направлением, называются векторными величинами или векторами.

Из курса физики вам знакомы такие величины.

Пусть на тело действует сила 8 Н. Надо еще знать, в каком направлении действует сила.

Стрелка показывает направление силы, а длина отрезка соответствует в выбранном масштабе числовому значению силы.

Рассмотрим отрезок произвольной величины. Его концы – граничные точки отрезка. На данном отрезке можно отметить 2 направления.

Чтобы выбрать одно из направлений, одну граничную точку отрезка назовем началом, другую – концом. Теперь будем считать, что отрезок направлен от начала к концу.

Отрезок, для которого обозначены начало и конец, называется направленным отрезком или вектором.

На рисунке вектор обозначается отрезком со стрелкой, показывающей направление вектора. Обозначается вектор двумя заглавными латинскими буквами со стрелкой над ними, например 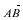, где А – начало вектора, В – конец вектора.

Вектор – направленный отрезок.

А – начало вектора

В В – конец вектора

Задание 1: Назовите векторы, изображенные на рис.85, 86.

Задание 2: (№406) Отметьте три точки А, В и С, не лежащие на одной прямой. навертите векторы АВ, ВС и АС.

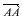
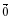
Также любая точка плоскости – вектор. В данном случае вектор называется нулевым, т.е начало вектора совпадает с его концом. Обозначается такой вектор двумя одинаковыми заглавными латинскими буквами — или .

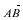
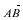
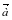
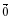
Длиной или модулем ненулевого вектора называется длина отрезка АВ. Длина вектора обозначается (). Длина нулевого вектора считается равной нулю: =0.

Коллинеарные векторы – это ненулевые векторы, если они лежат на параллельных прямых или на одной прямой: | | .

а) сонаправленные векторы.

б) противоположно направлены.

Т.к. у нулевого вектора начало и конец совпадают, поэтому определенного направления он не имеет.

Задание 3: По рис. 87-90 назвать виды векторов.

Ненулевые векторы называются равными, если их модули равны и они сонаправлены. Любые два нулевых вектора равны.

Задание 4: (№417) (Работа в парах) По рис. 97 назвать виды векторов.

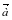
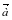
Пусть дана точка А и А – начало вектора . Тогда вектор отложен от точки А.

От любой точки М можно отложить вектор, равный данному вектору 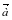, и притом только один.

5. Историческая справка.

Как институт без ректора,

Так геометрия без вектора!

Теория векторов развивалась в XIX в. параллельно с теорией систем линейных уравнений. Направленные отрезки использовал Арган (J.R. Argand, 1768–1822) в работе «Опыт некоторого представления мнимых величин … «, опубликованной в 1806 году. Эти отрезки Арган обозначал символами →a, →b и т.п. Мëбиус обозначал отрезок с началом в точке A и концом в точке B символом AB . Он считается одним из основателей теории векторов. Термин «вектор» ввел Гамильтон приблизительно в 1845 году. Он же определил скалярное и векторное произведения векторов в 1853 году.

6. Закрепление знаний.

Графически: № 407, 409, 411.

У доски: № 415, 418.

7. Самостоятельная работа учащихся.

Решить в парах № 419.

Задание на повторение: (из курса «Геометрия 7 класс»)

Фронтальный опрос «Дальше, дальше…». Класс разбит на 3 команды. За каждый верный ответ-жетон.

Что такое геометрия?

Что такое планиметрия?

Приведите примеры плоских и неплоских фигур.

Опишите понятие точка.

Опишите понятие прямая.

Опишите понятие плоскость.

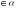
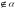
Что означает запись А, В?

Сформулируйте основное свойство расположения точки на прямой.

Как обозначается луч?

Какие лучи называются дополнительными?

Что такое отрезок?

Что такое концы отрезка?

В каких единицах измеряется отрезок?

Сформулируйте основное свойство измерения отрезков.

Что такое середина отрезка?

Что такое расстояние между двумя точками?

какая фигура называется углом?

Как обозначаются углы?

В каких единицах измеряются углы?

Какой угол называется острым?

Какой угол называется прямым?

Какой угол называется тупым?

Какой угол называется развернутым?

Сформулируйте основное свойство измерения углов.

Что такое биссектриса угла?

Какие углы называются равными?

8.Итоги урока. Рефлексия. Д/з.

Выучить п. 12, вопросы с.112-113.

Решить: на 7 баллов- № 408, 410, на 9 баллов- № 408, 410, 412, на 12 баллов- № 408, 410,

Сообщение « Из истории векторов».

Что ты понял сегодня на уроке?

Чего ты сегодня не понял на уроке?

При выполнении каких заданий ты ошибся и почему?

Укажи причины успехов и неудач своей деятельности.

Что вам дало изучение понятия вектор?

Каков смысл сегодняшнего урока?

Мировая наука начиналась с геометрии. Человек не может по настоящему развиваться культурно и духовно, если он не изучал в школе геометрию. Геометрия возникла не только из практических, но и духовных потребностей человека.

Тема: «Равные вектора».

Цель: — закрепить понятие вектора; коллинеарных, сонаправленных, равных векторов;

отработать навыки применения понятия вектор при решении задач.

— развитие умений выделять главное, сравнивать, обобщать, делать выводы, критически относиться к получаемой информации, аргументировать собственное высказывание;

— создание условий для формирования ответственного отношения к учебному

труду, умения работать в паре, микрогруппе.

1. Организационный момент

Мудр не тот, кто знает много, а тот, чьи знания полезны.

Ребята, послушайте, какая тишина!

Это в школе начались уроки.

Мы не будем тратить время зря,

И приступим все к работе.

Мы сюда пришли учиться,

Не лениться, а трудиться.

Проверка готовности к уроку.

2. Мотивация урока.

Девизом нашего урока является высказывание: “Есть в математике нечто, вызывающее человеческий восторг”, так как на уроках геометрии очень важно уметь, смотреть и видеть, замечать и отмечать различные особенности геометрических фигур. Даю “установку”: Развивать и тренировать свое геометрическое зрение.

Кто ничего не замечает,

Тот ничего не изучает.

Кто ничего не изучает,

Тот вечно хнычет и скучает.

3. Актуализация опорных знаний. Проверка д/з.(сверка с доской №420)

-Что такое вектор?

— Как он изображается на рисунках?

— Какой вектор называется нулевым?

— Что такое длина вектора?

— Какие векторы называются коллинеарными?

— Какие векторы называются равными?

? Какие из следующих величин являются векторными: скорость, масса, сила, время, температура, длина, площадь, работа? Докажите это.

Задание 1. Назовите векторы, укажите их начало и конец.

Задание 2.( обсуждение в парах) Укажите:

в) противоположно направленные;

д) равные по модулю;

4. Решение упражнений по теме «Понятие вектора. Модуль и направление вектора. Равные вектора».

решить устно: № 421( в группах),423,

решение у доски: 424, 425, 426,

6. Физминутка для глаз.

-Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке, классную доску по периметру против часовой стрелки, треугольник, изображенный на стенде по часовой стрелке и равный ему треугольник против часовой стрелки. Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа. Закройте глаза, сосчитайте до 5, откройте глаза и …

Мы ладонь к глазам приставим,
Ноги крепкие расставим.
Поворачиваясь вправо,
Оглядимся величаво.
И налево надо тоже
Поглядеть из под ладошек.
И – направо! И еще
Через левое плечо!
а теперь продолжим работу.

7. Самостоятельная работа учащихся.

Работа в парах. Решить № 430.

Задание на повторение: (из курса «Геометрия 7 класс»)

1)Назовите пары смежных углов и вертикальных углов:

2) Найти величины остальных углов.

8.Итоги урока. Рефлексия. Д/з.

Повторить п.12. Решить на 8 баллов- № 424, 427, на 12 баллов- № 424, 427, 431, 433.

Что вы узнали нового? На уроке:

вы сделали вывод …

вы пополнили словарный запас следующими терминами …

Тема урока: «Координаты вектора»

обучающая: ввести понятие координат вектора, координат равных векторов, координат противоположных векторов; формирование навыков решения простейших задач методом координат;

развивающая: развитие мыслительных операций (анализ, синтез, сравнение);

воспитательная: развивать у учащихся культуру речи, аккуратность ведения записей.

1. Организационный момент

Ребята, послушайте, какая тишина!

Это в школе начались уроки.

Мы не будем тратить время зря,

И приступим все к работе.

Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:

— Что есть больше всего на свете? – Пространство.

— Что быстрее всего? – Ум.

— Что мудрее всего? – Время.

— Что приятнее всего? – Достичь желаемого.

Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.

2. Мотивация урока.

Мы познакомились с понятием координат точки на плоскости. Сегодня на уроке мы узнаем о координатах вектора, равных и противоположных векторов, познакомимся с формулой для нахождения длины вектора.

3. Актуализация опорных знаний. Проверка д/з.(сверка с доской №434)

1. Дайте определение вектора

[Вектором или направленным отрезком называется отрезок для которого указано, какая из его граничных точек считается началом, а какая – концом.]

2 Длина или модуль ненулевого вектора АВ – это

[длина отрезка АВ]

3.Ненулевые вектора называются коллинеарными, если…

[они лежат либо на одной прямой, либо на параллельных прямых]

4.Сколько векторов равных данному можно отложить от точки

5. Два коллинеарных вектора направленные одинаково называются

6. Векторы называются равными, если…

[они сонаправлены и их длины равны]

— отгадайте слово: ровная, гладкая поверхность, когда человек отпускается в нравственном отношении, говорят о нём, что он катится по наклонной… (плоскости)

Под каким углом пересекаются координатные прямые х и у, образующие систему координат на плоскости?

Как называют каждую из этих прямых?

Ответ: координатную прямую х называют осью абсцисс, а координатную прямую у – осью ординат.

Как называют точку пересечения этих прямых?

Ответ: точку пересечения этих прямых называют началом координат.

Как называют пару чисел, определяющих положение точки на плоскости?

Ответ: эту пару чисел называют координатами точки.

Как называют первое число? Второе число?

Ответ: первое число – абсцисса точки,

второе число – ордината точки.

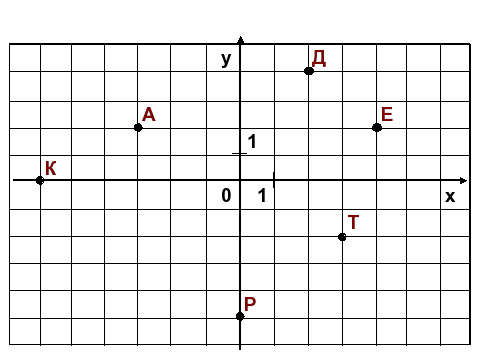
Задание: Назовите координаты точек. Найдите расстояние между точками А и Д.

4. Изучение нового материала.

Координаты вектора с началом в точке А и концом в точке В:

Равные векторы имеют равные соответствующие координаты:

Модуль (длина вектора). Задание: По рисунку определить длину вектора.

Из формулы расстояния между двумя точками следует, что для вектора (а₁; а₂):

Быстро встали, улыбнулись.

— Ну-ка, плечи распрямите,

— Вправо, влево повернитесь,

— Рук коленями коснитесь.

— Сели, встали. Сели, встали

— И на месте побежали.

6. Закрепление нового материала.

Решить № 445, 446, 447, 448, 452, 454.

Решить в парах № № 450.

8.Итоги урока. Рефлексия. Д/з.

Выучить п.13. Вопросы с.119. Решить на 8 баллов- № 449, 451, на 12 баллов- № 455, 459,

Что нового узнали на уроке?

— Оцените свои знания по таблице:

Тема: «Сложение и вычитание векторов»

Цель: — дать определение суммы и разности векторов; научить учащихся строить сумму двух данных векторов, используя правила треугольника и параллелограмма, содействовать формированию навыков выполнения действий над векторами;

— развитие графической культуры и вычислительных навыков школьников;

— воспитание навыков учебного труда.

1. Организационный момент

2. Мотивация урока.

3. Актуализация опорных знаний. Проверка д/з.(сверка с доской №434)

Что называют координатами данного вектора?

Что можно сказать о координатах равных векторов?

Как найти координаты вектора, если известны координаты его начала и конца?

Как найти модуль вектора, если известны его координаты?

Решить № 456, 460.

4. Формирование новых знаний.

1. Правило треугольника.

3. Правило параллелограмма

4. Свойства сложения векторов.

в) ( + ) + = + ( + ) .

Правилом треугольника сложения векторов называется следующий способ:
Пусть есть произвольные векторы ā и b. Надо от конца вектора a отложить вектор b`, равный вектору b. Тогда вектор, начало которого совпадает с началом вектора ā, а конец совпадет с концом вектора b`, будет суммой ā + b.

Векторное сложение можно производить также по правилу параллелограмма, равносильному правилу треугольника: при построении параллелограмма оба слагающих вектора откладывают от одной точки и они служат сторонами параллелограмма. Тогда диагональ параллелограмма, проведенная из той же точки, есть векторная сумма.

Вычитание векторов, как и вычитание чисел, — это действие, обратное сложению. Разность двух векторов и называется такой вектор , который в сумме с вектором дает вектор . Разность векторов и обозначается так: — . Построить разность векторов и можно следующим образом. Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда вектор и будет разностью — , поскольку

=+. Итак, == — = — .

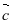
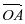
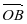
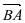
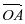
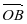
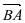
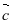
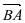
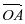
Вычитание векторов можно свести к сложению точно так же, как и в случае чисел а и b:

а — b = а + (- b), где числа b и + (- b) — противоположные.

Итак, нам надо доказать, что результат вычитания вектора из вектора тот же, что и результат сложения векторов а + (- b).

Чтоб глаза твои зоркие были,

Чтоб в очках тебе не ходить,

Эти лёгкие движенья

Вдаль посмотри и под ноги,

Вправо, влево побыстрей.

Удивимся, что такое?

И закроем их скорей.

А теперь по кругу быстро,

Словно стрелочка часов,

Проведём глазами дружно,

Ну, а дальше будь здоров!

6. Закрепление нового материала.

Решить № 458, 459, 470, 480.

Решить в парах № 484.

8.Итоги урока. Рефлексия. Д/з.

Выучить п. 14 . Вопросы с. 127 . Решить на 8 баллов- № 480, 471 , на 12 баллов- № 480, 471,485, 483.

Что нового узнали на уроке?

— Оцените свои знания по таблице:

Тема: «Умножение вектора на число»

Образовательные: рассмотрение правил треугольника и параллелограмма сложения векторов в пространстве, законы сложения векторов; изучение правил сложения нескольких векторов в пространстве и его применение при нахождении векторных сумм, не прибегая к рисункам; рассмотрение правил умножения вектора на число и основные свойства этого действия, а так же их применение при решении задач.

Развивающие: развитие памяти, математической речи, наблюдательности, развитие графических навыков у учащихся.

Воспитательные: формирование культуры ученического труда.

1. Организационный момент

Добрый день! Добрый час!

Как я рада видеть вас.

Прозвенел уже звонок

Друг на друга поглядели

И тихонько дружно сели.

2. Мотивация урока.

Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.

Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.

Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.

3. Актуализация опорных знаний. Проверка д/з.

1. Что называют суммой и разностью векторов?

2. Какие существуют способы нахождения суммы и разности векторов?

3. Каково взаимное расположение векторов при нахождении :

а) суммы двух векторов используя правило треугольника и правило параллелограмма?

б) разности двух векторов?

в) вектора противоположного данному?

4. Что называют длинной вектора?

Решить № 475, 490, 492.

4. Изучение нового материала.

1. Произведение вектора на число.

Определив сложение двух векторов, мы можем рассмотреть суммы вида: а+а, а+а+а и т.д.. Такие суммы, как и в алгебре, обозначаются 2а,3а и т.д. (рисунок1). Этот пример показывает, что удобно ввести операцию умножения вектора на число, и подсказывает, как дать соответствующее определение.

Произведением ненулевого вектора на число k называется такой вектор, длина которого равна  k*, причем векторы и сонаправлены при k  0 и противоположно направлены при k

Произведением нулевого вектора на любое число считается нулевой вектор.

2. Следствия из определения:

1. 1 = для любого вектора.

Действительно, если 0, то по определению 1 =1 = и т.к. k=1 0, то

1 1 =. Если =0, то1 =0 1 = для любого вектора.

2. (-1) = — для любого вектора .

Действительно, если 0, то (-1)  = -1= и т.к. k=-1 =0

(-1) = — для любого вектора .

3. Если k =0, то либо k=0, либо =0.

Действительно, если k =0, то  k= k=0, т.е. либо  k=0, либо =0, что и означает, либо k=0, либо =0.

4. Если k = k и k0, то =.

Действительно, если  k= k, то  k= k, отсюда =. Если k 0, то k, k, а т.к. k = k, .

Если же kk, k, а т.к. k = k, то.

Итак,= и , т.е. =

3. Законы умножения вектора на число

Умножение вектора на число подчиняется тем же законам, что и умножение чисел. Докажем три закона, справедливые для любых векторов и и любых чисел k и m.

1.( k + m) = k+ m ( I распределительный закон)

2. k( + ) = k+ k ( II распределительный закон)

3. (k m) = k (m) ( сочетательный закон)

5. Упражнение «Чудо-нос».

После слов «задержу дыхание» учащиеся делают вдох и задерживают дыхание. Учитель читает стихотворный текст, ребята только выполняют задание.

🌟 Видео

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Угол между диагоналями куба. Метод координат и векторов. Задачи на даче-15.Скачать

10 класс, 40 урок, Сложение и вычитание векторовСкачать

Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Новое задание профиля №2. Все, что нужно знать о векторах | Аня МатеманяСкачать

Сложение векторов. 9 класс.Скачать

О смысле комплексных чиселСкачать

10 класс, 38 урок, Понятие вектораСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

8 класс, 40 урок, Понятие вектораСкачать

Скалярное произведение векторов. 9 класс.Скачать

Векторы. Метод координат. Вебинар | МатематикаСкачать