что прямая, проходящая через точку М и середину стороны AD, перпендикулярна ВС.
Ответ:
Ну, ответ в прикреплённом файле.
Решение:
Пусть ABCD — данная трапеция, AD и BC — ее основания, O — точка пересечения диагоналей AC и BD этой трапеции. Докажем, что треугольники AOB и COD имеют одинаковую площадь. Для этого опустим из точек B и C на прямую AD перпендикуляры BP и CQ. Тогда площадь треугольника ABD равна.
P. S.
Считай, то что O = M, просто я в инете нашла только такую схему, ведь сама я их рисовать не умею. А решение я сама делала. Надеюсь ты хорошо сделаешь это ДЗ 😉
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать
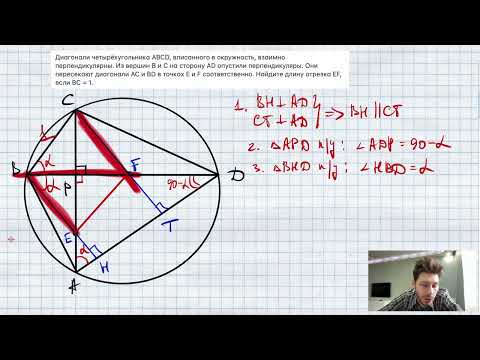
Четырехугольник ABCD вписан в окружность, его диагонали АС и BD взаимно перпендикулярны, а прямые АВ и CD пересекаются в точке О. Вычислите
Видео:Диагонали четырёхугольника ABCD, вписанного в окружность, взаимно перпендикулярны. Из вершин В и ССкачать
Ваш ответ
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать
решение вопроса
Видео:3 правила для вписанного четырехугольника #shortsСкачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,727
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Задание 26 Вписанный четырёхугольникСкачать
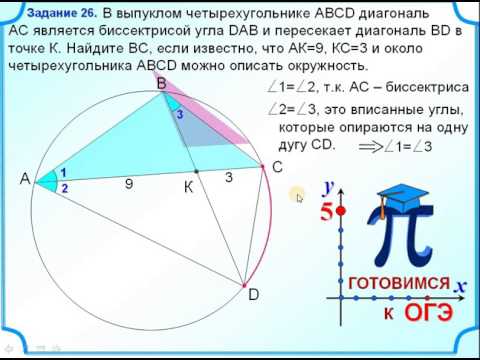
Диагонали ас и вд вписанного в окружность четырехугольника авсд взаимно перпендикулярны
Задание 16. Диагонали АС и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC = CD.
а) Докажите, что AB:BC=AP:PD.
б) Найдите площадь треугольника COD, где О — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, АВ = 5, а ВС = 5√2.
а) Так как стороны BC=CD, то и дуга BC равна дуге CD. На эти дуги опираются равные углы: BAC, CAD, CBD, CDB. Получаем подобные треугольники BPC и APD (по двум углам), следовательно, 
и
или 
(1)
Далее, треугольники BPC и ABC также подобны по двум углам, поэтому
или 
(2)
В результате из (1) и (2), имеем:
б) Так как BD – диаметр окружности, то треугольники BCD и ABD – прямоугольные с прямыми углами C и A соответственно. Также по условию задания BC=CD=5√2, получаем
Рассмотрим прямоугольный треугольник BAD, в котором AB=5, BD=10, следовательно, угол BDA=30°, а угол ODO1 = 15° (так как O – центр вписанной окружности, поэтому DO – биссектриса).
Далее, из равнобедренного треугольника BCD с основание BD получаем, что угол CDB=45°, следовательно, угол ODC=45+15=60°. Из прямоугольного треугольника ABD
и полупериметр треугольника ABD, равен:
Найдем отрезок DE=p-AB (как отрезок части касательной), имеем:
и радиус вписанной окружности:
Рассмотрим прямоугольный треугольник OED, из которого
Рассмотрим треугольник OCD, в котором 
, следовательно, треугольник ODC – равносторонний. Площадь этого треугольника, равна:
Ответ: 
📺 Видео
Геометрия Четырёхугольник ABCD со сторонами AB = 2 и CD = 5 вписан в окружность. Диагонали AC и BDСкачать
ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать
№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать
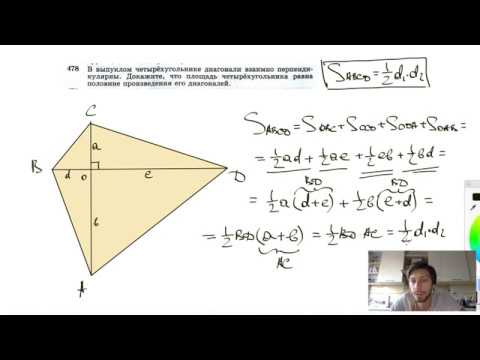
#58. Олимпиадная задача о четырехугольникеСкачать
Задание 26 Вписанный четырёхугольникСкачать
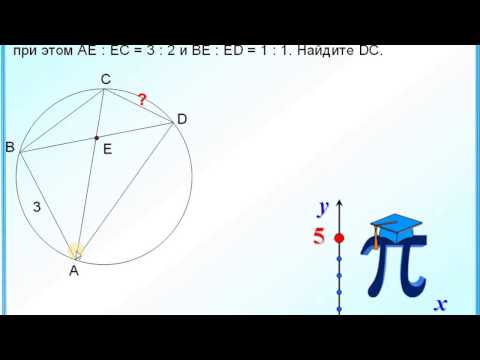
ОГЭ по математике 2024 геометрия | Разбор всех 16 заданийСкачать
МЕРЗЛЯК-8 ГЕОМЕТРИЯ. ОПИСАННАЯ И ВПИСАННАЯ ОКРУЖНОСТИ ЧЕТЫРЁХУГОЛЬНИКА. ПАРАГРАФ-10. ТЕОРИЯСкачать
Геометрия Диагонали AC и BD параллелограмма ABCD равны соответственно 24 см и 10 см AD = 13 смСкачать
Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать
№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать
Отрезки AC и BD – диаметры окружности с центром O ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать
№ 101-200 - Геометрия 9 класс КазаковСкачать
№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать
ЕГЭ Математика Задание 6#27935Скачать
