Продолжение стороны треугольника это

Треугольник. Остроугольный, тупоугольный и прямоугольный треугольник.

Катеты и гипотенуза. Равнобедренный и равносторонний треугольник.

Основные свойства треугольников. Сумма углов треугольника.

Внешний угол треугольника. Признаки равенства треугольников.

Признаки равенства прямоугольных треугольников.

Замечательные линии и точки в треугольнике: высоты, медианы,

биссектрисы, срединны e перпендикуляры, ортоцентр,

центр тяжести, центр описанного круга, центр вписанного круга.

Теорема Пифагора. Соотношение сторон в произвольном треугольнике.

Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

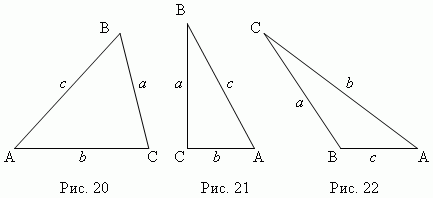
Если все три угла острые ( рис.20 ), то это остроугольный треугольник . Если один из углов прямой ( C, рис.21 ), то это прямоугольный треугольник; стороны a , b , образующие прямой угол, называются катетами; сторона c , противоположная прямому углу, называется гипотенузой. Если один из углов тупой ( B, рис.22 ), то это тупоугольный треугольник.

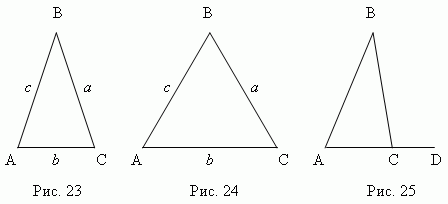
Треугольник ABC ( рис.23 ) — равнобедренный , если две его стороны равны ( a = c ); эти равные стороны называются боковыми, третья сторона называется основанием треугольника. Треугольник ABC ( рис.24 ) – равносторонний , если все его стороны равны ( a = b = c ). В общем случае ( a ≠ b ≠ c ) имеем неравносторонний треугольник.

Основные свойства треугольников. В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

В частности, все углы в равностороннем треугольнике равны.

3. Сумма углов треугольника равна 180 º .

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Из двух последних свойств следует, что каждый угол в равностороннем

Видео:Найдите третью сторону треугольникаСкачать

треугольнике равен 60 º.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

4. Продолжая одну из сторон треугольника ( AC , рис.25), получаем внешний

Видео:9 класс, 15 урок, Решение треугольниковСкачать

угол BCD . Внешний угол треугольника равен сумме внутренних углов,

Видео:Нахождение стороны прямоугольного треугольникаСкачать

не смежных с ним : BCD = A + B .

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

5. Любая сторона треугольника меньше суммы двух других сторон и больше

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

их разности ( a b – c; b b > a – c; c c > a – b ).

Признаки равенства треугольников.

Треугольники равны, если у них соответственно равны:

a ) две стороны и угол между ними;

b ) два угла и прилегающая к ним сторона;

Признаки равенства прямоугольных треугольников.

Д ва прямоугольных треугольника равны, если выполняется одно из следующих условий:

1) равны их катеты;

2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;

4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;

5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Замечательные линии и точки в треугольнике.

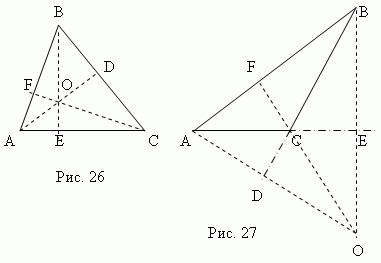
Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ). Эта сторона называется основанием треугольника . Три высоты треугольника всегда пересекаются в одной точке , называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника ( точка O , рис.26 ) расположен внутри треугольника, а ортоцентр тупоугольного треугольника ( точка O , рис.27 ) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

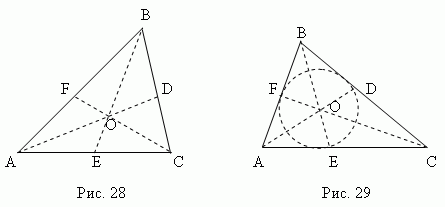
Медиана – это отрезок , соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника ( AD , BE , CF , рис.28 ) пересекаются в одной точке O , всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.

Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника ( AD , BE , CF , рис.29 ) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).

Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам ; например, на рис.29 AE : CE = AB : BC .

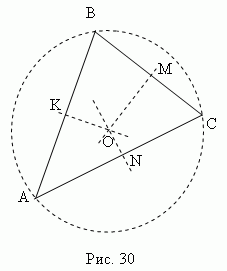
Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника АВС ( KO , MO , NO , рис.30 ) пересекаются в одной точке О, являющейся центром описанного круга ( точки K , M , N – середины сторон треугольника ABC ).

В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном — в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.

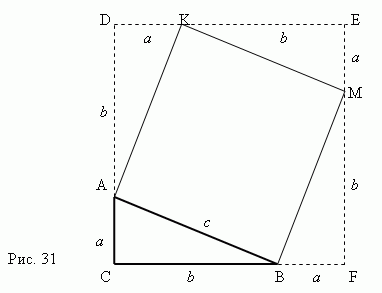
Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Доказательство теоремы Пифагора с очевидностью следует из рис.31. Рассмотрим прямоугольный треугольник ABC с катетами a , b и гипотенузой c .

Построим квадрат AKMB , используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF , сторона которого равна a + b . Теперь ясно, что площадь квадрата CDEF равна ( a + b ) 2 . С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB , то есть

и окончательно имеем:

Соотношение сторон в произвольном треугольнике.

В общем случае ( для произвольного треугольника ) имеем:

где C – угол между сторонами a и b .

Copyright © 2004 — 2012 Др. Юрий Беренгард. All rights reserved.

Видео:Задача про стороны треугольника. Геометрия 7 класс.Скачать

Обобщающий урок «Теоремы Менелая и Чевы»

Разделы: Математика

Цель:

• повторить и обобщить изученные теоремы;
• рассмотреть их применение при решении ряда задач;
• подготовка учащихся к вступительным экзаменам в ВУЗы;
• воспитывать эстетическое выполнение чертежей к задачам.

Оборудование: мультимедийный проектор. Приложение 1.

1. Организационный момент.

2. Проверка домашнего задания:

• доказательство теорем – 2 учащихся + 2 уч-ся – консультанты (проверяющие);
• решение домашних задач – 3 учащихся;
• работа с классом – устное решение задач:

Точка С₁ делит сторону АВ треугольника АВС в отношении 2 : 1. точка В₁ лежит на продолжении стороны АС за точку С, и АС = СВ₁. В каком отношении делит прямая В₁ С₁ сторону ВС? (на слайде 2).

Решение: По условиюИспользуя теорему Менелая, находим: .

В треугольнике АВС АD – медиана, точка О – середина медианы. Прямая ВО пересекает сторону АС в точке К.

В каком отношении точка К делит АС, считая от точки А? (на слайде 3).

Решение: Пусть ВD = DС = а, АО = ОD = m. Прямая ВК пересекает две стороны и продолжение третьей стороны треугольника АDС . По теореме Менелая .

В треугольнике АВС на стороне ВС взята точка N так, что NС = 3ВN; на продолжении стороны АС за точку А взята точка М так, что МА = АС. Прямая МN пересекает сторону АВ в точке F. Найдите отношение . (на слайде 4).

Решение: По условию задачи МА = АС, NС = 3 ВN. Пусть МА = АС = b, BN = k, NC = 3k. Прямая МN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая

.

На стороне PQ треугольника PQR взята точка N, а на стороне РR – точка L, причем NQ = LR. Точка пересечения отрезков QL и NR делит QR в отношении m : n, считая от точки Q. Найдите PN : PR. (на слайде 5).

Решение: По условию NQ = LR, . Пусть NA = LR = a, QF =km, LF = kn. Прямая NR пересекает две стороны треугольника PQL и продолжение третьей. По теореме Менелая

.

3. Отработка практических навыков.

1. Решение задач:

Докажите теорему: Медианы треугольника пересекаются в одной точке; точка пересечения делит каждую из них в отношении 2 : 1, считая от вершины. (рисунок 1 слайд 6).

Доказательство: Пусть АМ₁, ВМ₂, СМ₃ – медианы треугольника АВС. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что Тогда по теореме Чевы (обратной) отрезки АМ₁, ВМ₂ и СМ₃ пересекаются в одной точке. Имеем:

Итак, доказано, что медианы треугольника пересекаются в одной точке.

Пусть О – точка пересечения медиан. Прямая М₃С пересекает две стороны треугольника АВМ₂ и продолжение третьей стороны этого треугольника. По теореме Менелая

или .

Рассматривая теорему Менелая для треугольников АМ₁С и АМ₂С, мы получаем, что

. Теорема доказана.

Докажите теорему: Биссектрисы треугольника пересекаются в одной точке. (рисунок 2 слайд 6).

Доказательство: Достаточно показать, что . Тогда по теореме Чевы (обратной) AL_1, BL_2, CL₃ пересекаются в одной точке. По свойству биссектрис треугольника:

. Перемножая почленно полученные равенства, получаем: . Итак, для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке. Теорема доказана.

Докажите теорему: Высоты остроугольного треугольника пересекаются в одной точке. (рисунок 3 слайд 6).

Доказательство: Пусть АН₁, АН_2, АН₃ – высоты треугольника АВС со сторонами a, b, c. Из прямоугольных треугольников АВН₂ и ВСН₂ по теореме Пифагора выразим, соответственно, квадрат общего катета ВН₂, обозначив АН₂ = х, СН₂ = b – х.

(ВН₂) 2 = с 2 – х 2 и (ВН₂) 2 = а 2 – (b – х) 2 . приравнивая правые части полученных равенств, получаем с 2 – х 2 = а 2 – (b – х) 2 , откуда х = .

Тогда b –x = b — = .

Итак, АН₂ = , СН₂ = .

Аналогично рассуждая для прямоугольных треугольников АСН₂ и ВСН₃, ВАН₁ и САН₁, получим АН₃ = , ВН₃ = и ВН₁ = ,

СН₁ = .

Для доказательства теоремы достаточно показать, что . Тогда по теореме Чевы (обратной) отрезки АН₁, ВН₂ и СН₃ пересекаются в одной точке. Подставив в левую часть равенства выражения длин отрезков АН₃, ВН₃, ВН₁, СН₁, СН₂ и АН₂ через а, b, с, убеждаемся, что равенство Чевы для высот треугольника выполняется. Теорема доказана.

Задачи 5 – 7 самостоятельное решение 3 учащихся. (чертежи на экране).

2. остальные:

Докажите теорему: Если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон пересекаются в одной точке. (на рисунке 4 слайд 6).

Доказательство: Пусть А₁, В₁ и С₁ – точки касания вписанной окружности треугольника АВС. Для того, чтобы доказать, что отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:

. Используя свойство касательных, проведенных из одной точки, введем обозначения: ВС₁ = ВА₁ = х, СА₁ = СВ₁ = у, АВ₁ = АС₁ = z.

. Равенство Чевы выполняется, значит, указанные отрезки (биссектрисы треугольника) пересекаются в одной точке. Эту точку называют точкой Жергона. Теорема доказана.

3. Разбор задач 5, 6, 7.

Пусть АD – медиана треугольника АВС. На стороне АD взята точка К так, что АК : КD = 3 : 1. Прямая ВК разбивает треугольник АВС на два. Найдите отношение площадей этих треугольников. (на слайде 7 рисунок 1)

Решение: Пусть АD = DC = a, KD = m, тогда АК = 3m. Пусть Р – точка пересечения прямой ВК со стороной АС. Необходимо найти отношение . Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то = . По теореме Менелая для треугольника ADC и секущей РВ имеем: . Итак, = .

В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС = 4. А₁ и С₁ – точки касания, принадлежащие соответственно сторонам ВС и ВА. Р – точка пересечения отрезков АА₁ и СС₁. Точка Р лежит на биссектрисе ВВ₁. Найдите АР : РА₁.

(на слайде 7 рисунок 2)

Решение: Точка касания окружности со стороной АС не совпадает с В₁, так как треугольник АВС – разносторонний. Пусть С₁В = х, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (см рисунок) 8 – х + 5 – х = 4, х = .

Значит, С₁В = ВА₁ = , А₁С = 5 — = , АС₁ = 8 — = .

В треугольнике АВА₁ прямая С₁С пересекает две его стороны и продолжение третьей стороны. По теореме Менелая .

Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник. (на слайде 7).

Решение: Пусть в треугольнике АВС АВ = 5, ВС = 7, АС = 6. Угол ВАС лежит против большей стороны в треугольнике АВС, значит, угол ВАС – больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть О – точка пересечения биссектрис. Необходимо найти АО : ОD. Так как АD – биссектриса треугольника АВС, то , то есть BD = 5k, DС = 6k. так как BF – биссектриса треугольника АВС, то , то есть AF = 5m, FC = 7m. Прямая BF пересекает две стороны и продолжение третьей стороны треугольника ADC. По теореме Менелая .

4. Самостоятельное решение задач 9, 10, 11. – 3 учащихся.

Задача 12 (для всех оставшихся учащихся класса):

Биссектрисы ВЕ и АD треугольника АВС пересекаются в точке Q. Найдите площадь треугольника АВС, если площадь треугольника BQD = 1, 2АС = 3 АВ, 3ВС = 4 АВ. (рисунок 4 на слайде 7).

Решение: Пусть АВ = а, тогда АС = , ВС = . АD — биссектриса треугольника АВС, тогда , то есть BD = 2p, DC = 3p. ВЕ – биссектриса треугольника АВС, тогда , АЕ = 3 k, ЕС = 4k. В треугольнике ВЕС прямая АD пересекает две его стороны и продолжение третьей стороны. По теореме Менелая , , , то есть EQ = 9m, QB = 14m. Треугольники QBD и EBC имеют общий угол, значит , S_ЕВС = .

Треугольники АВС и ВЕС имеют равные высоты, проведенные из вершины В, значит, , тогда S_ABC = _.

5. Разбор задач 9, 10, 11.

Решение задач – практикум:

А. На сторонах ВС, СА, АВ равнобедренного треугольника АВС с основанием АВ взяты точки А_1, В₁, С_1, так что прямые АА₁, ВВ₁, СС₁ – конкурентные.

Докажите, что

По теореме Чевы имеем: (1 ).

По теореме синусов:, откуда СА₁ = СА .,

, откуда А₁В = АВ . , ,

откуда АВ₁ = АВ . , , откуда В₁С = ВС . , так как СА = ВС по условию. Подставив полученные равенства в равенство (1 ) получим:

.

Что и требовалось доказать.

В. На стороне АС треугольника АВС взята такая точка М, что АМ = ?АС, а на продолжении стороны ВС – такая точка N, что BN = СВ. В каком отношении точка Р – точка пересечения отрезков АВ и MN делит каждый из этих отрезков?

По теореме Менелая для треугольника АВС и секущей MN имеем:

. По условию следовательно ,

так как 0,5 . (-2) . х = 1, — 2х = — 2, х = 1.

Для треугольника MNC и секущей АВ по теореме Менелая имеем: по условию

значит, — , откуда, .

8. Самостоятельное решение задач: 1 вариант:

1. На продолжениях сторон АВ, ВС, АС треугольника АВС взяты соответственно точки С₁, А₁, В₁ так, что АВ = ВС₁, ВС = СА₁, СА = АВ₁. Найдите отношение в котором прямая АВ₁ делит сторону А₁С₁ треугольника А₁В₁С₁. (3 балла).

2. На медиане СС₁ треугольника АВС взята точка М. Прямые АМ и ВМ пересекают стороны треугольника соответственно в точках А₁ и В₁. Докажите, что прямые АВ и А₁В₁ параллельны. (3 балла).

3. Пусть на продолжении сторон АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В_1. Докажите, что точки А₁, В_1, С₁ лежат на одной прямой тогда и только тогда, когда выполняется равенство . (4 балла).

4. Используя теорему Чевы, докажите, что высоты треугольника или их продолжения пересекаются в одной точке. (4 балла).

5. Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля). (Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон). (5 баллов).

6. Пусть на сторонах АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В₁ так, что прямые АА₁, ВВ₁, СС₁ пересекаются в точке О. Докажите, что выполняется равенство . (5 баллов).

7. Пусть на ребрах АВ, ВС, СD и АD тетраэдра АВСD взяты соответственно точки А₁, В₁, С₁, D_1. Докажите, что точки А₁, В₁, С₁, D₁ лежат в одной плоскости тогда и только тогда, когда выполняется равенство (5 баллов).

1. Точки А₁ и В₁ делят стороны ВС и АС треугольника АВС в отношениях 2 : 1 и 1 : 2. Прямые АА₁ и ВВ₁ пересекаются в точке О. Площадь треугольника АВС равна 1. Найдите площадь треугольника ОВС. (3 балла).

2. Отрезок МN, соединяющий середины сторон АD и ВС четырехугольника АВСD делится диагоналями на три равные части. Докажите, что АВСD – трапеция, одно из оснований АВ или СD, которое в двое больше другого. (3 балла).

3. Пусть на стороне АВ и продолжении сторон ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В₁. Докажите, что прямые АА₁, ВВ₁, СС₁ пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство . (4 балла).

4. Используя теорему Чевы, докажите, что высоты треугольника или их продолжения пересекаются в одной точке. (4 балла).

5. Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля). (Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон). (5 баллов).

6. Пусть на сторонах АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁, В₁ так, что прямые АА₁, ВВ₁ и СС₁ пересекаются в точке О. Докажите, что выполняется равенство . (5 баллов).

7. Пусть на ребрах АВ, ВС, СD и АD тетраэдра АВСD взяты соответственно точки А₁, В₁, С₁, D_1. Докажите, что точки А₁, В₁, С₁, D₁ лежат в одной плоскости тогда и только тогда, когда выполняется равенство (5 баллов).

9. Домашнее задание: учебник § 3, № 855, № 861, № 859.

Видео:Найдите сторону треугольника на рисункеСкачать

Треугольник. Формулы и свойства треугольников.

Видео:№470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведенная кСкачать

Типы треугольников

По величине углов

По числу равных сторон

Видео:Уравнения стороны треугольника и медианыСкачать

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Видео:Найдите стороны треугольникаСкачать

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Видео:Теорема косинусов. Две стороны треугольника равны 4 см и 8 см, а угол ....Скачать

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Видео:Треугольники. 7 класс.Скачать

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

Связь между вписанной и описанной окружностями треугольника

Видео:Признаки равенства треугольников. 7 класс.Скачать

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Видео:Почему в треугольнике против большей стороны - больший угол ➜ ДоказательствоСкачать

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.