1. Высказывания с кванторами
2. Отрицание высказываний и высказывательных форм
- Высказывания с кванторами
В формулировках математических предложений часто встречаются слова: «каждый», «все», «некоторые», «хотя бы один». Например, свойство противоположных сторон прямоугольника формулируется так: «В любом прямоугольнике противоположные стороны равны», а о свойстве натуральных чисел мы говорили, что «некоторые натуральные числа кратны 3». Выясним, каков смысл этих слов и как они используются в математике.
Если задана высказывательная форма, то, чтобы превратить ее в высказывание, достаточно вместо каждой из переменных, входящих в форму, подставить ее значение. Например, если на множестве N натуральных чисел задана высказывательная форма А(х) – «число х кратно 5», то, подставив в нее вместо х число 20, мы получим истинное высказывание «число 20 кратно 5». Если же в эту высказывательную форму подставить вместо х число 17, мы получим ложное высказывание «число 17 кратно 5».
Однако существуют и другие способы получения высказываний из высказывательных форм.
Если перед высказывательной формой «число х кратно 5» поставить слово «всякое», то получится предложение «всякое число х кратно 5».Относительно этого предложения можно задать вопрос, истинно оно или ложно. Значит, оно является высказыванием, причем ложным.
Выражение «для всякого х» в логике называется квантором общности по переменной х (переменная может быть обозначена и другой буквой) и обозначается символом ∀х.
Запись (∀х.) А(х) означает: «для всякого значения х предложение А(х) – истинное высказывание.». Иногда эту запись дополняют обозначением множества Х, на котором задана высказывательная форма А(х), и тогда предложение можно читать:
а) для всякого х из множества Х истинно А(х);
б) всякий элемент из множества Х обладает свойством А.
Выражение «существует х такое, что…» в логике называется квантором существованияпо переменной х (переменная может быть обозначена и другой буквой) и обозначается символом ∃х.
Запись (∃х) А(х) означает: «существует такое значение х, что А(х) – истинное высказывание». Иногда эту запись дополняют обозначением множества Х, на котором задана высказывательная форма А(х), и тогда предложение (∃х) А(х) можно читать:
а) существует такое х из множества Х, что истинно А(х);
б) хотя бы один элемент х из множества Х обладает свойством А.
Заметим, что в математике наряду со словом «всякий» употребляют слова «каждый», «любой», а вместо слова «существует» используют слова «некоторые», «найдется», «есть», «хотя бы один».
Итак, если задана одноместная высказывательная форма А(х), то чтобы превратить ее в высказывание, достаточно связать квантором общности или существования содержащуюся в ней переменную. Если же высказывательная форма содержит несколько переменных, то перевести ее в высказывание можно, если связать квантором каждую переменную. Например, если дана высказывательная форма «х > у», то для получения высказывания надо связать квантором обе переменные: например, (∀х) (∃у) х > у или (∃х) (∃у) х > у.
Однако важно уметь не только переходить от высказывательной формы к высказыванию с помощью кванторов, но и распознавать их логическую структуру. Дело в том, что кванторы содержатся в формулировках определений, теорем и других математических предложений, хотя часто только подразумеваются. Например, в формулировке теоремы «Вертикальные углы равны» квантора в явном виде нет, но предполагается, что данное утверждение справедливо для всех вертикальных углов. Записывая коммутативное свойство сложения в виде а + b = b + а, подразумевают, что оно справедливо для любых чисел а и b.
Задача 1. Выявить логическую структуру следующих высказываний:
а) Некоторые нечетные числа делятся на 5.
б) Произведение двух любых последовательных натуральных чисел кратно 2.
в) В прямоугольнике диагонали равны.
Решение: а) (∃х∈Х) х ⋮5; б) (∀х∈ N) х(х+1) ⋮2; в) (∀х∈ Х) А(х).
Выясним теперь, как устанавливают значения истинности высказываний, содержащих кванторы.
Рассмотрим высказывание с квантором общности — (∀х∈ Х) А(х). Чтобы убедиться в истинности этого высказывания, надо показать, что множество истинности ТА высказывательной формы А(х) совпадает с множеством Х (ТА = Х). Чтобы убедиться в ложности высказывания (∀х∈ Х) А(х), достаточно показать, что ТА ≠ Х, т.е. показать, что существует такое значение х ∈ Х, при котором высказывательная форма обращается в ложное высказывание.
Задача 2. Установить, истинны или ложны следующие высказывания:
а) Для каждого х из множества значение выражения (4 –х):( 2х + 1) есть число целое.
б) Произведение двух любых последовательных натуральных чисел кратно 2.
в) Всякое натуральное число делится на 5.
а) Путем перебора всех возможных случаев установлено, что при заданных значениях х выражение принимает целое значение, т.е. высказывание истинное.
б) Высказывание истинно.
в) Высказывание ложно. Для этого достаточно привести хотя бы один пример.
В математике говорят, что в ложности данного высказывания мы убедились, приведя контрпример.
Вообще истинность высказывания с квантором общности устанавливается путем доказательства. Показать ложность таких высказываний можно, приведя контрпример.
Задача 3. Установить, истинны или ложны следующие высказывания:
а) Среди треугольников есть прямоугольные.
б) Некоторые прямоугольные треугольники являются равносторонними.
а) Высказывание истинное.
б) Высказывание ложное.
Вообще истинность высказывания с квантором существования устанавливается при помощи конкретного примера. Показать ложность таких высказываний можно, проведя доказательство.
- Отрицание высказываний и высказывательных форм
Пусть предложение А – высказывание. Если перед сказуемым данного предложения поставить частицу «не» либо перед всем предложением поставить слова «неверно, что», то получится новое предложение, которое называется отрицанием данного и обозначается Ā (читают: «не А» или «неверно, что А).
Определение. Отрицанием высказывания А называется высказывание Ā, которое ложно, когда высказывание А истинно, и истинно, когда высказывание А – ложно.
Таблица истинности отрицания имеет вид:
| А | Ā |
| и | л |
| л | и |
Из данного определения следует, что предложение и его отрицание не могут быть ни одновременно истинны, ни одновременно ложны.
Построим отрицание ложного высказывания «число 28 делится на 9:
А) Число 28 не делится на 9.
Б) Неверно, что число 28 делится на 9.
Высказывания, которые мы получили, истинные. Значит, отрицание данного предложения построено правильно.
Рассмотрим теперь правила построения отрицания конъюнкции и дизъюнкции высказываний. Если перед всем составным высказыванием поставим слова «неверно, что», то, безусловно, получим его отрицание. А как быть с частицей «не»? Можно ли поставить перед сказуемым составного предложения и получить его отрицание? На примере можно показать, что нельзя.



| А | В | А∧В |  А∧В А∧В |  А А |  В В |   А∨ В А∨ В |
| и | и | и | л | л | л | л |
| и | л | л | и | л | и | и |
| л | и | л | и | и | л | и |
| л | л | л | и | и | и | и |

Про высказывания вида А∧В и А∨ В говорят, что они равносильны, и пишут



Аналогично можно доказать, что имеет место равносильность



Эти равносильности носят название законов де Моргана.
Из них вытекает следующее правило построения отрицания конъюнкции и дизъюнкции: чтобы построить отрицание конъюнкции (дизъюнкции), достаточно заменить отрицаниями составляющие ее высказывания, а союз «и» («или») заменить союзом «или» («и).
Задача 1. Построить отрицание высказывания «число 28 делится на 9 или на 6».
1 способ: «неверно, что число 28 делится на 9 или на 6».
2 способ: воспользуемся законом де Моргана: «число 28 не делится на 9 и не делится на 6».
Как быть, если высказывания содержат кванторы? Строить отрицания высказываний при помощи частицы «не» перед сказуемым нельзя. Остается другой путь – перед всем предложением ставим слова «неверно, что». Например, дано высказывание всякий прямоугольный треугольник является равнобедренным». Его отрицанием будет высказывание «неверно, что всякий прямоугольный треугольник является равнобедренным». Это предложение имеет тот же смысл, что и предложение «некоторые прямоугольные треугольники не являются равнобедренными».
Отрицанием высказывания «некоторые прямоугольные треугольники не являются равнобедренными» является высказывание «неверно, что некоторые прямоугольные треугольники не являются равнобедренными», которое имеет тот же смысл, что и предложение «все прямоугольные треугольники не являются равнобедренными».
Вообще, если дано предложение ∀(х) А(х), то его отрицанием будут предложения




Получаем две равносильности:
 |  |
 |  |
Из них вытекает правило: для того чтобы построить отрицание высказывания, начинающегося с квантора общности (существования), достаточно заменить его кантором существования (общности) и построить отрицание предложения, стоящего после квантора.
Задача 2. Построить отрицание высказывания «некоторые однозначные числа делятся на 10».
1) «неверно, что некоторые однозначные числа делятся на 10»
2) «все однозначные числа не делятся на 10».
Последнее, о чем пойдет речь, — это отрицание высказывательных форм.

 |
обозначим А(х) (читают: «не А(х) или неверно, что А(х)». Предложение А(х) будет обращаться в истинное высказывание лишь при тех значениях х из множества Х, при которых А(х) – ложно. Таким образом, Т Ā = Т´ А – множество истинности предложения
А(х), а Т ´ А – дополнение множества Т А до множества Х.
Доказательство этого равенства мы опускаем.
Пусть, например, на множестве натуральных чисел задана высказывательная форма А(х) – «число х кратно 5». Тогда ее отрицанием будет предложение «число х не кратно 5» (или «неверно, что число х кратно 5»), истинное при всех значениях х, которые не кратны 5.
Лекция 8. Теоремы
1. Отношения следования и равносильности между предложениями
2. Структура теоремы. Виды теорем
3. Необходимые и достаточные условия. Рассуждения от противного. Правильные и неправильные рассуждения.
4. Основные выводы
- Отношения следования и равносильности между предложениями
Рассмотрим две высказывательные формы: «число х кратно 4» и «число х кратно 2», заданные на множестве N натуральных чисел.
Как связаны между собой эти два предложения?
Можно сказать так: из того, что число х кратно 4, следует, что х кратно 2. Это мы можем утверждать, потому что знаем – при всех значениях х, при которых истинно предложение «число х кратно 4», будет истинно и предложение «число х кратно 2». В этом случае говорят, что данные предложения находятся в отношении логического следования.
Определение. Высказывательная форма В(х) следует из высказывательной формы А(х), если В(х) обращается в истинное высказывание при всех тех значениях х, при которых А(х) истинна.
Если А и В – высказывания, тогда говорят, что из А следует В, если всякий раз, когда А истинно, истинно и В.
Для обозначения отношения логического следования используется знак ⇒. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) ⇒ В(х), прочитать которое можно по разному:
1) Из А(х) следует В(х).
2) Всякое А(х) есть В(х).
3) Если А(х), то В(х).
4) В(х) есть следствие А(х).
5) А(х) есть достаточное условие для В(х).
6) В(х) есть необходимое условие для А(х).
Например, утверждение о том, что из предложения «число х кратно 4», следует предложение «число х кратно 2», можно сформулировать еще так:
— Всякое число, которое кратно 4, кратно и 2.
— Если число кратно 4, то оно кратно и 2.
— Кратность число 2 есть следствие кратности его 4.
— Кратность числа 4 есть достаточное условие для его кратности 2.
— Кратность числа 2 есть необходимое условие для его кратности 4.
Последние два предложения часто формулируют в следующей форме:
— Для того чтобы число было кратно 2, достаточно, чтобы оно было кратно 4.
— Для того чтобы число было кратно 4, необходимо, чтобы оно было кратно 2
Так как одно и то же утверждение «из А(х) следует В(х)» можно прочитать по-разному, надо уметь переходить от одной его формулировки к другой, не меняя смысла.
Задача 1. Данные предложения переформулируйте, используя различные способы прочтения утверждения А(х) ⇒ В(х):
Всякий квадрат является прямоугольником.
А(х) – «четырехугольник – квадрат» и В(х) – «четырехугольник – прямоугольник».
1) Из того, что четырехугольник – квадрат, следует, что он прямоугольник.
2) Если четырехугольник – квадрат, то он прямоугольник
3) Четырехугольник является прямоугольником – это следствие того, что четырехугольник – квадрат.
4) Для того чтобы четырехугольник был прямоугольником, достаточно, чтобы он был квадратом.
5) Для того чтобы четырехугольник был квадратом, необходимо, чтобы он был прямоугольником.
Как и любое высказывание, предложение А(х) ⇒ В(х) может быть истинным или ложным. Но так как оно может быть сформулировано в виде «всякое А(х) есть В(х)», то его истинность устанавливается путем доказательства, а с помощью контрпримера – что оно ложно.
Определение. Предложения А(х) и В(х) равносильны, если из предложения А(х) следует предложение В(х), а из предложения В(х) следует предложение А(х).
Для обозначения отношения равносильности используется знак ⇔. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) ⇔ В(х), прочитать которое можно по-разному:
1) А(х) равносильно В(х).
2) А(х) тогда и только тогда, когда В(х).
3) А(х) – необходимо и достаточное условие для В(х).
4) В(х) — необходимое и достаточное условие для А(х).
Например, утверждение о том, что предложение «число делится на 3» и «сумма цифр в записи числа делится на 3» равносильны, можно сформулировать еще так:
— Число делится на 3 тогда и только тогда, когда сумма цифр в его записи делится на 3.
— Для того чтобы число делилось на 3, необходимо и достаточно, чтобы сумма цифр в его записи делилась на 3.
С теоретико-множественной точки зрения высказывание А(х) ⇔ В(х) означает, что если ТА – множество истинности высказывательной формы А(х), а ТВ – множество истинности высказывательной формы В(х), то ТА = ТВ.
Например, уравнения 3х(х-2) = 0 и 3х(х-2)(х+3) = 0 равносильны на множестве целых неотрицательных чисел, потому что множество их решений .
Заметим, что мы рассматриваем понятия логического следования и равносильности для одноместных высказывательных форм. Для предложений, содержащих две и более переменных, эти понятия определяются аналогично.
Отметим также, что знак ⇔ мы использовали раньше, в частности, рассматривая логическую структуру явных определений понятий. Мы установили, что ее можно представить в виде а⇔ в. Определение порождает два равносильных предложения.



- Структура теоремы. Виды теорем.
Понятие логического следования позволяет уточнить ряд вопросов, связанных с предложениями, которые в математике называют теоремами.
Теорема– это высказывание, истинность которого устанавливается посредством рассуждения (доказательства).
С логической точки зрения теорема представляет собой высказывание вида А ⇒ В, где А и В – высказывательные формы с одной или несколькими переменными. Предложение А называют условием теоремы, а предложение В – ее заключением.
Например, условием теоремы «если четырехугольник является прямоугольником, то в нем диагонали раны» является предложение «четырехугольник – прямоугольник, а заключением – предложение «в таком четырехугольнике диагонали равны».
В рассмотренном примере теорема была сформулирована с помощью слов «если …, то …». Но, как нам известно, утверждение А ⇒ В можно сформулировать и по-другому. Например, рассмотренную теорему можно сформулировать так: «во всяком прямоугольнике диагонали равны» или «для того, чтобы четырехугольник был прямоугольником, необходимо, чтобы его диагонали были равны». Есть и другие способы, но удобнее теорему формулировать в виде «если …, то …», поскольку сразу видно ее условие (что дано) и заключение (что надо доказать).
В математике кроме теорем используются предложения, называемые правилами и формулами. Выясним, чем они отличаются от теоремы.
Рассмотрим, например, такую теорему из школьного курса алгебры: «если а – любое число и k, n – натуральные число, то справедливо равенство аⁿ•аʰ = аⁿ⁺ʰ». Для того чтобы этой теоремой удобнее было пользоваться, при выполнении различных преобразований ее формулируют в виде правила: «при умножении степеней с одинаковыми основаниями показатели складываются» или записывают только формулу.
Учитель должен уметь разворачивать изучаемые в начальной школе правила (формулы) и формулировать соответствующие им теоремы. Например, правило деления суммы на число: «для того чтобы разделить сумму на число, можно разделить на это число каждое из слагаемых и полученные результаты сложить». К этой формулировке иногда добавляют формулу: (а + b): с = а : с + b: с. Так как этот материал изучают в начальной школе, то надо отчетливо понимать, что числа могут быть только целыми неотрицательными, причем с ≠ 0. Кроме того, воспользоваться правой частью этого равенства можно при условии, что а кратно с и b кратно с.
Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если В, то А», которое называют обратным данному. Однако не всегда это предложение является теоремой. Рассмотрим, например, теорему: «если четырехугольник является прямоугольником, то в нем диагонали равны». Построим предложение, обратное данному: «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником». Это высказывание ложное, в чем можно убедиться, приведя контрпример: в равнобедренной трапеции диагонали равны, но трапеция не является прямоугольником.
Рассмотрим теперь теорему «в равнобедренном треугольнике углы при основании равны». Обратное ей предложение таково: «если в треугольнике углы при основании равны, то этот треугольник – равнобедренный». Оно, как известно, истинное и поэтому является теоремой. Ее называют теоремой, обратной данной.
Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если не А, то не В», которое называют противоположным. Но не всегда это предложение является теоремой. Например, предложение, противоположное теореме «если четырехугольник является прямоугольником, то в нем диагонали равны», будет ложным: «если четырехугольник не является прямоугольником, то в нем диагонали не равны».
В том случае, если предложение, противоположное данному, будет истинно, его называют теоремой, противоположной данной.
Таким образом, если для теоремы А ⇒ В сформулировать обратное или противоположное предложения, то их надо доказывать (и тогда их можно называть соответственно обратной и противоположной теоремами) или опровергать.
Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если не В, то не А», которое называют обратным противоположному. Например, для теоремы «если четырехугольник является прямоугольником, то в нем диагонали равны» предложение, обратное противоположному, будет таким: «если в четырехугольнике диагонали не равны, то он не является прямоугольником». Это, как известно, предложение истинное и, следовательно, является теоремой. Ее называют обратно противоположной данной.


Эту равносильность называют законом контрапозиции. Мы принимаем его без доказательства. Согласно этому закону, предложение, обратно противоположное какой-либо теореме, также является теоремой, и, значит, вместо данной теоремы можно доказывать теорему, обратно противоположную данной.
Кроме того, из закона контрапозиции следует, что предложение, обратное данному, и предложение, противоположное данному, одновременно истинны либо одновременно ложны. Поэтому, рассматривая их, достаточно доказать (или опровергнуть) какое-нибудь одно; тем самым будет доказано (опровергнуто) другое.
Заметим, что если для данной теоремы А ⇒ В существует обратная В ⇒А, то их можно соединить в одну А ⇔ В, и тогда в формулировке будут использованы слова «необходимо и достаточно», «тогда и только тогда, когда». Например: «треугольник будет равнобедренным тогда и только тогда, когда в нем углы при основании равны».
С другой стороны, если теорема имеет вид А ⇔ В, то это значит, что она состоит из двух взаимно обратных теорем А ⇒ В и В ⇒А и, следовательно, ее доказательство сводится к доказательству двух указанных теорем.
Заметим также, что если условие или заключение данной теоремы представляет собой конъюнкцию или дизъюнкцию, то, чтобы получить предложение, противоположное данному, нужно учитывать правила построения отрицания конъюнкции или дизъюнкции. Например, дана теорема «если число делится на 3 и 4, то оно делится на 12». Предложение, противоположное данному, можно сформулировать так: «если число не делится на 12, то оно не делится на 3 или не делится на 4».
- Основные выводы
Основные понятия: высказывание, значение истинности высказывания, высказывательная форма, область определения высказывательной формы, множество истинности высказывательной формы, элементарные высказывания, логические связки, составные высказывания, конъюнкция высказываний и высказывательных форм, дизъюнкция высказываний и высказывательных форм, квантор общности, квантор существования, отрицание высказываний и высказывательных форм, отношение логического следования между предложениями, отношение равносильности между предложениями.
Видео:Вписанные четырехугольники. 9 класс.Скачать

ПРАКТИЧЕСКАЯ РАБОТА. ВЫСКАЗЫВАНИЯ С КВАНТОРАМИ. ОТРИЦАНИЕ ВЫСКАЗЫВАНИЙ И ВЫСКАЗЫВАТЕЛЬНЫХ ФОРМ
Цель. Рассмотреть правила определения значения истинности составного высказывания и высказывательных форм с кванторами.
Теоретическая часть
Вопросы к изучению
1. Высказывания с кванторами.
2. Истинность высказываний с кванторами.
3. Отрицание высказываний и высказывательных форм.
Основные понятия темы
Ø квантор общности;
Ø квантор существования;
Ø отрицание высказываний и высказывательных форм.
Правила
Ø нахождения множества истинности составных высказывательных форм:
Т А Ù В = ТА Ç Т В, Т А Ú В = ТА È Т В, 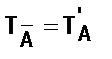
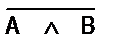
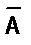
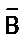

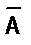
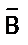
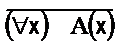
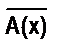
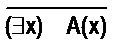
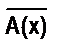
Обозначения
» х – «для всякого х», квантор общности;
$ х — «существует х такое, что …», квантор существования;
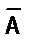
Практическая часть
1. В высказывании «всякий прямоугольник является четырехугольником» выделите квантор и высказывательную форму. Переформулируйте данное высказывание, заменив слово «всякий» его синонимом.
2. В высказывании «хотя бы одно из чисел первого десятка составное» выделите квантор и высказывательную форму. Переформулируйте данное высказывание, заменив квантор «хотя бы одно» его синонимом.
3. Прочитайте следующие записи, заменив символические обозначения кванторов общности и существования их словесными выражениями: а) («х ÎR) х 2 – 1 = (х+1) (х-1); б) ($ у Î R) 5 + у =5; в) («у ÎR) у + 3 > 0; г) ($ х Î N) х +3 2 + вх +с = 0 имеет хотя бы один корень.
5. Запишите, используя символы, следующие высказывания и определите их значение истинности: а) Всякое число, умноженное на нуль, есть нуль; б) Произведение любого числа и единицы равно этому числу; в) При делении нуля на любое другое число получается нуль; г) Квадрат любого числа неотрицателен.
6. Установите, какие из нижеприведенных высказываний истинны, а какие ложны: а) Во всяком четырехугольнике диагонали равны; б) Существуют числовые выражения, значения которых нельзя найти; в) При делении на 5 некоторых натуральных чисел в остатке получается 7; г) Любое однозначное число является решением неравенства х + 2 > 1.
7. Докажите или опровергните следующие высказывания: а) Существуют уравнения, множество решений которых пусто; б) Всякое целое число является натуральным; в) Сумма любых двух четных чисел есть число четное; г) Хотя бы одно натуральное число является решением уравнения 7: х =2.
8. Данные ниже высказывания взяты из учебников математики для начальных классов. Выясните, какие из них содержат (в явном или неявном виде) квантор и как следует устанавливать их значение истинности (указать только способ и обосновать его выбор): а) От перестановки слагаемых сумма не изменяется; б) Два соседних слагаемых можно заменять их суммой; в) Площадь прямоугольника равна произведению его длины на ширину; г) Существуют четные числа; д) Некоторые числа делятся на 4; е) Среди многоугольников есть треугольники.
9. Сформулируйте отрицания следующих предложений: а) Число 123 делится на 9; б) При делении числа 32 на 5 в остатке получится 7; в) 3+2 в, в > а; г) существуют две непараллельные прямые; д) у всех прямоугольников все углы прямые; е) ни для какого натурального числа а не найдется натуральное число в такое, что а + в 34 353637>
Дата добавления: 2021-01-26 ; просмотров: 347 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:#58. Олимпиадная задача о четырехугольникеСкачать

Высказывания с кванторами
В параграфе, который мы изучаем, рассматриваются различные вилы математических предложений. Мы выяснили, что среди них выделяют высказывания и высказывательные формы, которые могут быть элементарными и составными. Мы узнали также, как устанавливают значение истинности таких высказываний и как находят множество истинности высказывательных форм. Но мы, конечно, не исчерпали все многообразие формулировок математических предложений и, значит, не знаем многих правил обращения с ними. Например, почему можно одну и ту же теорему о равенстве вертикальных углов формулировать по-разному:
1)Вертикальные углы равны.
2)Если углы вертикальные, то они равны.
3)Для того чтобы углы были равны, достаточно, чтобы они были вертикальными.
4)Для того чтобы углы были вертикальными, необходимо, чтобы они были равны.
Или: почему истинность предложения «сумма трех любых последовательных натуральных чисел делится на 3» надо доказывать, а чтобы убедиться в истинности предложения «некоторые натуральные числа делятся на 3», достаточно привести конкретный пример?
Чтобы ответить на эти вопросы, необходимо более глубокое изучение математических предложений и, прежде всего, высказываний с кванторами.
В формулировках математических предложений часто встречаются слова: «каждый», «все», «некоторые», «хотя бы один». Например, свойство противоположных сторон прямоугольника формулируется так: «в любом прямоугольнике противоположные стороны равны», а о свойстве натуральных чисел мы говорили, что «некоторые натуральные числа кратны 5». Выясним, каков смысл этих слов и как они используются в математике.
Если задана высказывательная форма, то, чтобы превратить ее в высказывание, достаточно вместо каждой из переменных, входящих в форму подставить ее значение. Например, если на множестве N натуральных чисел задана высказывательная форма А(х) — «число х кратно 5», то, подставив в нее вместо х число 20, мы получим истинное высказывание «число х кратно 5». Если же в эту высказывательную форму подставить вместо х число 17, мы получим ложное высказывание «число 17 кратно 5».
Однако существуют и другие способы получения высказываний из высказывательных форм.
Если перед высказывательной формой «число х кратно 5» поставить слово «всякое», то получится предложение «всякое число х кратно 5» Относительно этого предложения можно задать вопрос, истинно оно или ложно. Значит, предложение «всякое число х кратно 5» (х Î N) — высказывание, причем ложное.
Выражение «для всякого л» в логике называется квантором общности по переменной х (переменная может быть обозначена и другой буквой) и обозначается символом » х.
Запись («х) А(х) означает: «для всякого значения х предложение А(х) — истинное высказывание». Иногда эту запись дополняют обозначением множества X, на котором задана высказывательная форма А(х) и тогда предложение («х Î X) А(х) можно читать:
а) для всякого х из множества X истинно А(х);
б) всякий элемент из множества X обладает свойством А.
Выражение «существует х такое, что . » в логике называется квантором существования по переменной х (переменная может быть обозначена и другой буквой) и обозначается символом $х.
Запись ($х) А(х) означает: «существует такое значение х, что А(х)- истинное высказывание». Иногда эту запись дополняют обозначением множества X, на котором задана высказывательная форма А(х), и тогда предложение ($х$ X) А(х) можно читать:
а) существует такое х из множества X, что истинно А(х);
б) хотя бы один элемент х из множества X обладает свойством А.
Заметим, что в математике наряду со словом «всякий» употребляют слова «каждый», «любой», а вместо слова «существует» используют слова «некоторые», «найдется», «есть», «хотя бы один».
Обратим внимание на особенность употребления в математике слова «некоторый». В обычной речи, говоря «некоторые», имеют в виду «по меньшей мере один, но не все», в математике же слово «некоторые» означает «по меньшей мере один, но, может быть, и все».
Итак, если задана одноместная высказывательная форма А(х), то чтобы превратить ее в высказывание, достаточно связать квантором общности или существования содержащуюся в ней переменную. Если же высказывательная форма содержит несколько переменных, то перевести ее в высказывание можно, если связать квантором каждую переменную. Например, если дана высказывательная форма A(x) то для получения высказывания надо связать квантором обе переменные: например, («х) ($у) х> у или ($х) ($у) х > у.
Однако важно уметь не только переходить от высказывательной формы к высказыванию с помощью кванторов, но и распознавать высказывания, содержащие кванторы, и выявлять их логическую структуру. Дело в том, что кванторы содержатся в формулировках определений теорем и других математических предложений, хотя часто только и подразумеваются. Например, в формулировке теоремы «Вертикальные углы равны» квантора в явном виде нет, но предполагается, что данное утверждение справедливо для всех вертикальных углов. Записывая коммутативное свойство сложения в виде а + b — b + а, подразумевают что оно справедливо для любых чисел a и b.
Задача 1. Выявить логическую структуру следующих высказываний:
а) Некоторые нечетные числа делятся на 5.
б) Произведение двух любых последовательных натуральных чисел кратно 2.
в) В прямоугольнике диагонали равны.
Решение. а) В этом предложении имеется квантор существования, он выражен словом «некоторые», и высказывательная форма «нечетные числа делятся на 5», заданная на множестве X нечетных чисел. Обозначим высказывательную форму символом А(х), тогда логическая структура данного предложения такова: ($х Î X) А(х). Если предложение А(х) записать, используя символы: «х:5», то исходное высказывание можно представить в таком виде: ($х Î X) х:5, где X — множество нечетных чисел.
б) В данном предложении имеется квантор общности, он представлен словом «любой», и высказывательная форма «произведение двух последовательных натуральных чисел кратно 2», заданная на множестве N натуральных чисел. Обозначим ее А(х). Тогда логическая структура данного высказывания такова: ($х Î N) А(х). И если А(х) представить в виде х(х + 1):2, то заданное предложение можно записать так: ($ х Î N) х(х + 1):2.
в) В заданном высказывании квантора в явном виде нет, но подразумевается, что свойством «иметь равные диагонали» обладают любые прямоугольники, следовательно, этот квантор общности можно включить в заданное высказывание, не изменив его сути: «в любом прямоугольнике диагонали равны». Тогда его структура такова: ($ х Î X) А(х),где X — множество прямоугольников, А(х) — высказывательная форма «в прямоугольнике диагонали равны».
Выясним теперь, как устанавливают значения истинности высказываний, содержащих кванторы.
Рассмотрим сначала высказывание с квантором общности, т.е. высказывание вида ($ хÎ X) А(х). В нем утверждается, что для любого х из множества X истинно А(х), поэтому, чтобы убедиться в истинности этого высказывания, надо показать, что множество истинности ТА высказывательной формы А(х) совпадает с множеством X (ТА — X). Чтобы убедиться в ложности высказывания ($ х Î X) А(х), достаточно оказать, что ТА ¹ X, т.е. показать, что существует такое значение х Î X, при котором высказывательная форма обращается в ложное высказывание.
Задача 2. Установить, истинны или ложны следующие высказывания:
а) Для каждого х из множества значение выражения (4 — х): (2х + 1) есть число целое.
б) Произведение двух любых последовательных натуральных чисел кратно 2.
в) Всякое натуральное число делится на 5.
Решение. а) Если мы хотим убедиться в истинности данного высказывания, то надо показать, что при подстановке каждого числа из множества в выражение (4 — х): (2х + 1) получается целое число. Имеем:
если х = 0,то(4-0):(2-0 + 1) = 4:1 =4;
если х — 1,то (4- 1):(2-1 + 1) = 3:3 = 1;
если х = 4,то(4-4):(2-4 + 1) = 0:9 = 0.
Действительно, значение выражения (4 — х):(2х + 1) при всех заданных значениях х есть число целое. Установили мы это путем перебора всех возможных случаев.
б) Воспользуемся результатом задачи 1 (случай б) и представим данное высказывание в таком виде: («х Î N) х(х + 1): 2.
Мы не знаем, истинно оно или ложно, поэтому рассмотрим несколько случаев. Если х = 1, то произведение 1×2 кратно 2, так как на 2 делится второй множитель. Если х = 2, то произведение 2×3 тоже кратно 2, так как на 2 делится первый множитель. Если х = 7, то и в этом случае 7 × 8 кратно 2, поскольку второй множитель 8 делится на 2. Исходя из рассмотренных случаев, можно предположить, что данное высказывание истинное, но убедиться в этом путем перебора (как в первом предложении) нельзя, поскольку невозможно перебрать все натуральные значения х. Будем рассуждать. Из двух последовательных натуральных чисел одно обязательно четное. Но если в произведении один из множителей делится на 2, то, как известно, и все произведение делится на 2. Следовательно, при любом натуральном х произведение х(х+1) делится на 2.
в) Высказывание «всякое натуральное число делится на 5» — ложное. Убедиться в этом можно, назвав натуральное число, которое не делится на 5, например число 12.
В математике говорят, что в ложности данного высказывания мы убедились, приведя контрпример.
Вообще истинность высказывания с квантором общности устанавливается путем доказательства. Показать ложность таких высказываний можно, приведя контрпример.
Заметим, что доказательство истинности высказываний, содержащих квантор общности, можно выполнять различными методами. Решая задачу 2, мы использовали перебор всех возможных случаев и рассуждения. Эти и другие методы доказательства будут рассматриваться нами позже, в § 4.
Выясним, как устанавливается значение истинности высказывании, содержащих квантор существования. В высказывании ($х Î X) А(х) утверждается, что в множестве X есть такой элемент х, которой обладает свойством А. Поэтому оно будет истинно, если множество истинности высказывательной формы А<х) не пусто (ТА ¹ Æ). Для того чтобы показать это, достаточно найти такое значение переменной х, при котором высказывательная форма А(х) обращается в истинное высказывание, т.е. привести пример.
Высказывание ($х Î X) А(х) ложно в том случае, когда ТА =Æ.
Убедиться в этом можно лишь путем доказательства.
Задача 3. Установить, истинны или ложны следующие высказывания:
а) Среди треугольников есть прямоугольные.
б) Некоторые прямоугольные треугольники являются равносторонними.
Решение: а) Данное высказывание содержит квантор существования, который выражен словом «есть». Чтобы убедиться в истинности такого высказывания, достаточно привести пример. В данном случае прямоугольный треугольник можно начертить.
б) В этом случае квантор существования выражен словом «некоторые». Если считать данное высказывание истинным, то надо привести пример, т.е. попытаться начертить треугольник, который был бы одновременно прямоугольным и равносторонним. Из того, что это не удается начертить, еще не следует вывод о ложности данного высказывания. В этом надо убедиться путем доказательства.
Действительно, если треугольник прямоугольный, то в нем один угол равен 90°, а в равностороннем все углы 60°. Следовательно, ни один прямоугольный треугольник не может быть равносторонним. Поэтому данное высказывание ложное.
Вообще истинность высказывания с квантором существования устанавливается при помощи конкретного примера. Чтобы убедиться в ложности такого высказывания, необходимо провести доказательство.
Заметим, что убедиться в ложности высказывания — это значит опровергнуть его.
Упражнения
1.В высказывании «всякий прямоугольник является четырехугольником» выделите квантор и высказывательную форму. Переформулируйте данное высказывание, заменив слово «всякий» его синонимом.
2.В высказывании «хотя бы одно из чисел первого десятка составное» выделите квантор и высказывательную форму. Переформулируйте данное высказывание, заменив квантор «хотя бы одно» его синонимом.
3.Прочтите следующие записи, заменив символические обозначения кванторов общности и существования их словесными выражениями:
а) («хÎR) х 2 — 1 = (х + 1)(х — 1);
в) («у Î R) у + 3 > 0;
г) ($х е N) х + 3 2 + bх + с = 0 имеет хотя бы один корень.
5. Запишите, используя символы, следующие высказывания и определите их значения истинности:
а) Всякое число, умноженное на нуль, есть нуль.
б) Произведение любого числа и единицы равно этому числу.
в) При делении нуля на любое другое число получается нуль.
г) Квадрат любого числа неотрицателен.
6. Укажите способы установления значения истинности высказываний, содержащих кванторы, заполнив таблицу:
| Структура высказывания Значение истиности | («хÎХ)А(х) | ($хÎХ)А(х) |
| и | ||
| л |
7. Установите, какие из нижеприведенных высказываний истинны, а какие ложны:
а) Во всяком четырехугольнике диагонали равны.
б) Существуют числовые выражения, значения которых нельзя найти.
в) При делении на 5 некоторых натуральных чисел в остатке получается 7.
г) Любое однозначное число является решением неравенства х + 2 > 1
8. Докажите или опровергните следующие высказывания:
а) Существуют уравнения, множество решений которых пусто.
б) Всякое целое число является натуральным.
в) Сумма любых двух четных чисел есть число четное.
г) Хотя бы одно натуральное число является решением уравнения 7:х=2.
9. Данные ниже высказывания взяты из учебников математики для начальных классов. Выясните, какие из них содержат (в явном или неявном виде) квантор и как следует устанавливать их значение истинности (указать только способ и обосновать его выбор):
а) От перестановки слагаемых сумма не изменяется.
б) Два соседних слагаемых можно заменять их суммой.
в) Площадь прямоугольника равна произведению его длины на ширину.
г) Существуют четные числа.
д) Некоторые числа делятся на 4.
е) Среди многоугольников есть треугольники.
Не нашли, что искали? Воспользуйтесь поиском:
🔥 Видео
Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Свойство и признак вписанного четырехугольникаСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

Описанные четырехугольники. 9 класс.Скачать
8 класс, 3 урок, ЧетырехугольникСкачать

№759 Дан произвольный четырехугольник MNPQ. Докажите, что:Скачать

Миникурс по геометрии. ЧетырехугольникиСкачать

№950. Докажите, что четырехугольник MNPQ является параллелограммом,Скачать

3 правила для вписанного четырехугольника #shortsСкачать

№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Виды четырёхугольниковСкачать

№400. Докажите, что если в четырехугольнике все углы прямые, то четырехугольник — прямоугольник.Скачать

Симедиана. Гармонические четырехугольники. | Олимпиадная математикаСкачать

Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

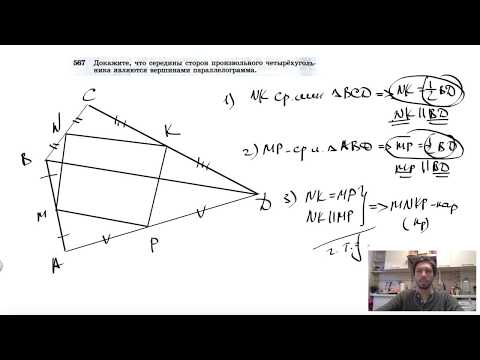
№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
Четырехугольники. Вебинар | МатематикаСкачать
