Доказать равенство треугольников биссектриса (3 видео)

Теорема о биссектрисе треугольника. Доказательство

Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:

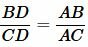Доказать равенство треугольников биссектриса

(1)

Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:

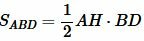(3)

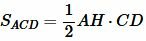(4)

Построим следующее соотношение

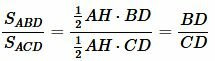(5)

С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:

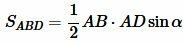(6)

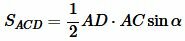(7)

Построим следующее соотношение используя формулы (6) и (7):

(8)

Из формул (5) и (8) получим соотношение (1).

Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).

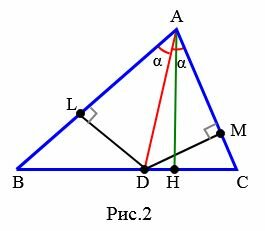Тогда площади треугольников ABD и ACD можно найти из формул:

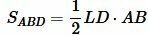(9)

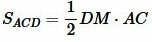(10)

Построим следующее соотношение

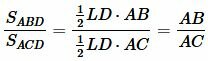(11)

Из формул (5) и (11) получим соотношение (1).

Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):

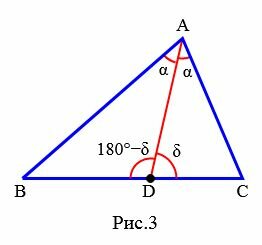Применяя теорему синусов для треугольников ABD и ACD можем записать:

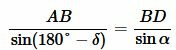(12)

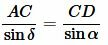(13)

Поделив (12) на (13) и учитывая, что ( small sin(180°-delta)=sin delta , ) (см. статью Формулы приведения тригонометрических функций онлайн) получим равенство (1).

Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.

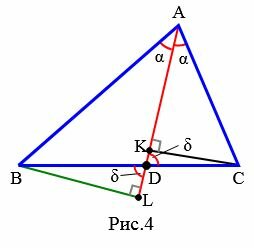Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (( small &angle; ALB= &angle; AKC ,;; &angle; BAL= &angle; CAK ) ). Тогда имеем:

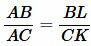(14)

Рассмотрим, далее, треугольники BLD и CKD. Они также подобны поскольку ( small &angle; BLD= &angle; CKD ,) а углы BDL и CDK равны так как они вертикальные. Тогда имеет место следующее соотношение:

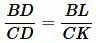(15)

Из равенств (14) и (15) получаем:

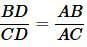Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.

Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:

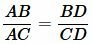(16)

Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:

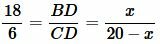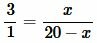(17)

Методом перекресного умножения упростим (17) и решим:

Содержание

№ 23. Докажите равенство треугольников по углу, биссектрисе этого угла и стороне, прилежащей к этому углу.
Признаки равенства треугольников с использованием медианы, биссектрисы и высоты
Скачать:
Предварительный просмотр:
🔥 Видео

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

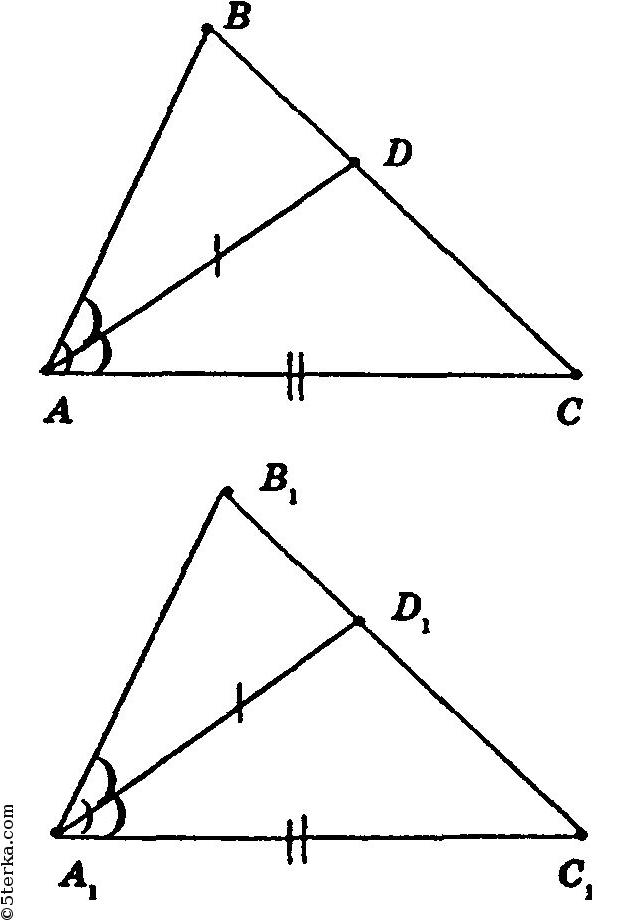
№ 23. Докажите равенство треугольников по углу, биссектрисе этого угла и стороне, прилежащей к этому углу.

Пусть AD = A₁D₁ — равные биссектрисы, ∠A = ∠A₁, AC = A₁C₁ — равные стороны.

AD = A₁D₁, АС = А₁С₁. (по условию: AD = A₁D₁ — равные биссектрисы, AС = A₁C₁ — равные прилежащие стороны).

Таким образом, ΔADC = ΔА₁D₁C₁ по 1-му признаку равенства треугольников, откуда ∠С = ∠С₁ как лежащие против равных сторон в равных треугольниках)

Таким образом, ΔABC = ΔА₁В₁С₁ по 1-му признаку равенства треугольников, что и требовалось доказать.

Решебник по геометрии за 7 класс (А.В. Погорелов, 2001 год),
задача №23
к главе «§ 3. Признаки равенства треугольников».

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Признаки равенства треугольников с использованием медианы, биссектрисы и высоты

Признаки равенства треугольников с использованием медианы, биссектрисы и высоты. Решетников Михаил Сергеевич, Харютченко Данил Александрович. Муниципальный этап.

Видео:Признаки равенства треугольников. 7 класс.Скачать

Скачать:

Вложение	Размер
Признаки равенства треугольников с использованием медианы, биссектрисы и высоты	1.67 МБ

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Предварительный просмотр:

МУНИЦИПАЛЬНЫЙ ЭТАП XI ВСЕРОССИЙСКОГО ДЕТСКОГО КОНКУРСА
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИХ И ТВОРЧЕСКИХ РАБОТ
«ПЕРВЫЕ ШАГИ В НАУКЕ»

Секция: информационные технологии; математика;

Тема: Признаки равенства треугольников с использованием медианы, биссектрисы и высоты

Авторы: Решетников Михаил Сергеевич, МОУ «Октябрьская СОШ им. Ю. Чумака», 8 класс

Харютченко Данил Александрович, МОУ «Октябрьская СОШ им. Ю. Чумака», 8 класс

Научный руководитель: Шевченко Елена Михайловна, учитель математики МОУ «Октябрьская СОШ им. Ю. Чумака»

Место выполнения работы: Белгородская область, Белгородский район, поселок Октябрьский

Признаки равенства треугольников с использованием медианы, биссектрисы и высоты

Треугольник – одна из самых простых и загадочных геометрических фигур. Вот уже два с половиной тысячелетия открываются его новые и новые свойства. Со времен «Начал» Евклида геометрия строится на основе трех признаков равенства треугольников. Исходя из того, что в треугольнике выделяют шесть основных элементов: три внутренних угла и три соответственно противолежащие им стороны, равенство треугольников устанавливается по равенству трех из шести элементов. Три следующих признака являются фундаментом геометрии:

по двум сторонам и углу между ними;
по стороне и прилежащим к ней углам;
по трём сторонам.

Эти признаки отличаются простотой формулировки и часто применяются при решении задач базового уровня. Рассматривая более сложные задачи, приходится фактически «изобретать велосипед», дважды или трижды применять известные признаки, конструируя из них решение. Это приводит к следующему выводу: известных трех признаков не всегда достаточно.

Если учесть, что для каждого треугольника однозначно определяются три медианы, три биссектрисы и три высоты, то число элементов треугольника увеличивается до 15. В связи с этим возникает следующая гипотеза: наряду с основными тремя признаками равенства треугольников можно сформулировать и доказать новые признаки равенства треугольников с использованием медианы, биссектрисы и высоты, знание которых поможет в решении многих геометрических задач.

Объектом данного исследования является треугольник и его элементы, в том числе медианы, биссектрисы и высоты; предмет исследования – признаки равенства треугольников.

сформулировать и доказать новые признаки равенства треугольников;

обосновать эффективность применения новых признаков равенства треугольников при решении геометрических задач.

проанализировать определения и свойства медианы, биссектрисы и высоты;
выявить зависимость между равенством отдельных элементов и равенством треугольников;
определить типы геометрических задач, при решении которых целесообразно применение полученных признаков.

В работе применялись методы научного исследования: анализ, сравнение, математическое моделирование.

Для доказательства новых признаков равенства треугольников использовались только первый, второй и третий признаки равенства треугольников, что обеспечивает простоту доказательства и доступность данной работы для широкого круга школьников.