Даны 2 параллельные прямые и точка м не лежащая на ней

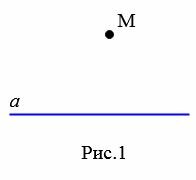
Рассмотрим прямую a и точку M, не лежащую на этой прямой (Рис.1). Докажем, что через точку M можно провести прямую, параллельную прямой a.

Проведем через точку M прямую c, перпендикулярно прямой a, и прямую b, перпендикулярно прямой c (Рис.2).

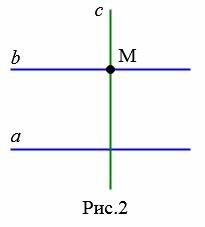Поскольку a и b перпендикулярны прямой с, то они параллельны (статья Перпендикулярные прямые Теорема 1 и статья Параллельные прямые. Признаки параллельности прямых Определение 1). Таким образом через точку M проходит прямая, параллельная прямой a.

Возникает вопрос, существует ли другая прямая, проходящая через точку M параллельно прямой a. Интуитивно ясно, что если немного повернуть прямую b вокруг оси M, то прямые b и a пересекутся. Но доказать это утверждение до сих пор не удалось. основываясь на стальных аксиомах геометрии.

Таким образом имеем это утверждение в виде аксиомы:

Аксиома 1. Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.

Следствие 1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

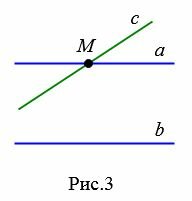Доказательство. Пусть заданы параллельные прямые a и b и пусть прямая c пересекает a в точке M (Рис.3). Докажем, что прямая c пересекает и прямую b.

Предположим обратное, т.е. c не пересекает b. Тогда получается, что через точку M проходят две прямые a и c параллельно прямой b, что невозможно (Аксиома 1). Следовательно прямая с пересекает и прямую b.

Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны.

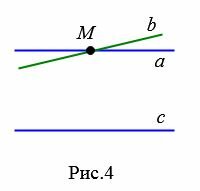Действительно. Предположим, что прямые a и b параллельны прямой c. Докажем, что прямая a параллельна прямой b. Предположим обратное, т.е. прямые a и b пересекаются в точке M (Рис.4). Тогда получается, что через точку M проходят две прямые, параллельные прямой c. Но это невозможно (Аксиома 1). Значит прямые a и b параллельны.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

10 класс. Геометрия. Параллельные прямые в пространстве.

10 класс. Геометрия. Параллельные прямые в пространстве.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:№86. Даны две пересекающиеся прямые а и b и точка А, не лежащая на этих прямых.Скачать

1. Тема урока

Решение простейших задач на параллельность прямой и плоскости.

Видео:№11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие черезСкачать

2. Определение параллельных прямых

Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (Рис. 1.).

Видео:10 класс, 3 урок, Некоторые следствия из аксиомСкачать

3. Теорема о параллельных прямых

Теорема о параллельных прямых.

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Пояснение к теореме

Дана прямая а, и точка М, не лежащая на ней: (Рис. 2.). Тогда через точку М проходит только одна прямая b, которая параллельная прямой а.

Видео:№149. Даны прямая а, точка В, не лежащая на ней, и отрезок PQ. Постройте точку М на прямой a такСкачать

4. Лемма

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Пояснение к лемме

Даны две параллельные прямые а и b. Прямая а пересекает плоскость в точке М. Лемма утверждает, что прямая b тоже пересекает плоскость в некоторой точке, назовем ее N (Рис. 3.).

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

5. Теорема о трех параллельных прямых

Теорема о параллельности трех прямых.

Если две прямые параллельны третьей, то они параллельны.

Пояснение к теореме.

Даны три прямые а, b, с, такие, что а параллельна с и b параллельна с (Рис. 4.). Теорема утверждает, что прямая а параллельна прямой b.

Видео:№35. Через точку М, не лежащую на прямой а, проведены две прямые, не имеющие общих точек с прямой а.Скачать

6. Случаи взаимного расположения прямой и плоскости

Аксиома А2: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости

Из аксиомы А2 вытекают три случая взаимного расположения прямой и плоскости.

1) Прямая а целиком лежит в плоскости α: (Рис. 5.).

2) Прямая а имеет одну общую точку с плоскостью α:. Другими словами, прямая а и плоскость α пересекаются (Рис. 6.).

3) Прямая a не имеет общих точек с плоскостью α: (Рис. 7.).

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

7. Определение параллельности прямой и плоскости

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Видео:Параллельность прямых. 10 класс.Скачать

8. Признак параллельности прямой и плоскости

Теорема (признак параллельности прямой и плоскости)

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Пояснение к признаку.

Дана плоскость , прямая а, которая параллельна прямой b, лежащей в плоскости (Рис. 8.). Согласно признаку параллельности прямой и плоскости, этого достаточно, чтобы прямая а была параллельна всей плоскости.

Видео:№94. Даны две скрещивающиеся прямые и точка В, не лежащая на этих прямых. Пересекаются ли плоскостиСкачать

9. Утверждение 1

Из данного признака вытекает два утверждения, полезных для решения задач.

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Дана плоскость и прямая а, которая параллельна плоскости (Рис. 9.). Через прямую а можно провести много плоскостей, которые пересекают плоскость . Проведем через прямую а плоскость . Согласно утверждению, линия пересечения плоскостей и – прямая b будет параллельна прямой а.

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

10. Утверждение 2

Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Есть две параллельные прямые а и b и плоскость . Одна из параллельных прямых, например, прямая а, параллельна плоскости . Отсюда следует, согласно утверждению, что прямая b либо параллельна плоскости (Рис. 10.), либо лежит в плоскости (Рис. 11.).

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

11. Задача 1

Задача 1.

Параллельные прямые а и b лежат в плоскости . Докажите, что прямая с, пересекающая прямые а и b, также лежит в плоскости .

Дано: а || b,

Доказать:

Доказательство: (Рис. 12.)

Точка А прямой с, принадлежит и прямой а, а значит, и плоскости . Точка В прямой с принадлежит прямой b, а значит, и плоскости . Так как две точки прямой с принадлежат плоскости , то и вся прямая лежит в плоскости , в силу аксиомы А2.

Видео:Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

12. Задача 2

Задача 2.

Стороны AB и BC параллелограмма ABCD пересекают плоскость . Докажите, что прямые AD и DC также пересекают плоскость .

Дано: ABCD – параллелограмм,

Доказать: прямые AD и DC пересекают плоскость .

Доказательство: (Рис. 13.)

Обозначим плоскость АВС как . Тогда плоскости и пересекаются по прямой MN. Прямая АВ пересекается с плоскостью , и прямые АВ и CD параллельны (как стороны параллелограмма). Тогда, согласно лемме, прямая CD также пересекается с плоскостью . Аналогично, прямая ВCпересекается с плоскостью , и прямые ВС и АD параллельны (как стороны параллелограмма). Тогда, согласно лемме, прямая АD также пересекается с плоскостью , что и требовалось доказать.

Давайте найдем эти точки пересечения. Пусть прямая CD пересекается с плоскостью в точке Q, а прямая АD пересекается с плоскостью в точке F.

Плоскости и пересекаются по прямой MN, значит все их общие точки лежат на этой прямой. Продолжим прямые CD и АD до их пересечения с прямой MNи получим соответственно точки Q и F (Рис. 14.).

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

13. Задача 3

Задача 3.

Средняя линия трапеции лежит в плоскости , не совпадающей с плоскостью . Пересекаются ли прямые, содержащие основания трапеции, с плоскостью ?

Дано: ABCD – трапеция, MN – средняя линия.

Найти: пересекаются ли прямые AD и ВC плоскость .

Вспомним, что средняя линия трапеции параллельна ее основанием. Значит, прямые AD и MN параллельны, а прямая MN принадлежит плоскости . Значит, по признаку параллельности прямой и плоскости, AD параллельна плоскости .

Аналогично, прямые ВC и MN параллельны, а прямая MN принадлежит плоскости . Значит, по признаку параллельности прямой и плоскости, ВC параллельна плоскости .

Ответ задачи: нет, не пересекаются.

Видео:№91. Через каждую из двух параллельных прямых a и b и точку М, не лежащую в плоскости этих прямыхСкачать

14. Задача 4

Задача 4.

Точка D не лежит плоскости прямоугольника KLMN. Доказать, что MN || DKL.

Дано: KLMN – прямоугольник,

Доказать: MN || DKL

Доказательство: (Рис. 16.)

Прямые KL и MN параллельны, а прямая KL принадлежит плоскости DKL. Следовательно, по признаку параллельности прямой и плоскости, MN параллельна плоскости DKL, что и требовалось доказать.

Видео:Стереометрия - это ПРОСТО! Урок 1. Аксиомы Теоремы Задачи. Геометрия 10 классСкачать

15. Итоги урока

Итак, мы рассмотрели теорию о параллельности прямой и плоскости, применили эту теорию к решению задач. Далее эта теория будет использована при рассмотрении вопроса о параллельности плоскостей.

Видео:№416. Даны две точки А и В, симметричные относительно некоторой прямой, и точка М.Скачать

Даны две параллельные прямые а и б и точка М не лежащая ни на одной из них?

Геометрия | 10 — 11 классы

Даны две параллельные прямые а и б и точка М не лежащая ни на одной из них.

Точка М лежит в одной плоскости с прямыми а и б, если через точку М можно провести прямую, пересекающую.

1) хотя бы одну из данных прямых.

2) только одну из данных прямых.

2) две данные прямые.

3) две данные прямые.

Видео:Аксиома параллельных прямых | Геометрия 7-9 класс #28 | ИнфоурокСкачать

1а Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются?

1а Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

2а Через точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной прямой, и притом только одна.

3а Если одна из двух параллельных прямых пересекает третью прямую, то и другая прямая пересекает эту прямую.

4а Две прямые, пересекающие третью прямую, пересекаются между собой.

5а Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

6а Если две прямые перпендикулярны третьей, то они параллельны друг другу.

7в Если одна из двух параллельных прямых пересекает третью прямую, то другая прямая лежит в одной плоскости с первой и третьей прямыми.

8в Две непараллельные прямые, пересекающие третью прямую, пересекаются между собой.

9в Если две параллельные прямые пересекаются третьей, то все три прямые лежат в одной плоскости.

10с Если параллельные прямые лежат в одной плоскости, то и прямая, имеющая общую точку с одной из них, лежит в этой же плоскости.

11с Три попарно непересекающиеся и непараллельные прямые лежат в трех разных плоскостях.

12с Две непараллельные прямые, пересекающие две данные параллельные прямые, пересекаются между собой.

Помогите пожалуйста, нужны все правильные ответы!

Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

1) Любые три различные прямые проходят через одну общую точку?

1) Любые три различные прямые проходят через одну общую точку.

2) Существует точка плоскости, не лежащая на данной прямой, через которую нельзя провести на плоскости ни одной прямой, параллельной данной.

3) Если угол равен 47°.

То смежный с ним угол равен 47°.

4) Через любые две различные точки плоскости можно провести прямую.

5) Существуют две различные прямые, не проходящие через одну общую точку.

Выберите номера верных утверждений.

Даны прямая и точка, не лежащая на этой ипрямой?

Даны прямая и точка, не лежащая на этой ипрямой.

Докажите, что все прямые, проходящие через эту точку и пересекающие данную прямую, лежат в одной плоскости.

Через точку, не лежащую на прямой, можно провести : 1) две прямые, параллельные данной прямой ; 2) только одну прямую, параллельную данной ; 3) ни одной прямой, параллельной данной ; 4) множество пара?

Через точку, не лежащую на прямой, можно провести : 1) две прямые, параллельные данной прямой ; 2) только одну прямую, параллельную данной ; 3) ни одной прямой, параллельной данной ; 4) множество параллельных прямых.

Выберите верные утверждения?

Выберите верные утверждения.

А) Прямая, не лежащая в данной плоскости и параллельная какой либо прямой на плоскости, параллельна самой плоскости.

Б) Плоскость, проходящая через одну из двух параллельных прямых, параллельна другой прямой.

В) Через точку, не принадлежащую плоскости, можно провести бесконечное число прямых, параллельных данной плоскости.

Г) Через одну из двух параллельных прямых можно провести плоскость, параллельную другой прямой, и только одну.

Д) Если две прямые параллельны одной плоскости, то они параллельны друг другу.

Помогите даны две различные прямые, пересекающиеся в точке А?

Помогите даны две различные прямые, пересекающиеся в точке А.

Докажите, что все прямые, пересекающие обе данные прямые и не проходящие через точку А, лежат в одной плоскости.

Помогите пожалуйста34?

A) Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

B) В любом треугольнике каждая сторона больше суммы двух других сторон.

C) Если две различные прямые имеют общую точку, то через них можно провести множество плоскостей.

D) Через четыре точки не лежащие на одной прямой можно провести плоскость и притом только одну.

Прямые в пространстве параллельны если они лежат в одной плоскости и имеют две общие точки

b) Через точку пространства можно провести прямую параллельную данной и при том только одну.

C) Если две параллельные прямые пересекают третью, то все они параллельны

d) Если две прямые не пересекаются и не лежат в одной плоскости, то они скрещивающиеся.

Прямая и плоскость называются параллельными, если они имеют две общие точки.

B) Если прямая не лежащая в данной плоскости, параллельна какой — нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

C) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей не параллельна данной прямой.

D) Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая пересекает эту плоскость.

Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости , то такие плоскости пересекаются.

B) Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны

c) Отрезки параллельных прямых заключенных между параллельными плоскостями пересекаются.

D) Две плоскости называются параллельными если они имеют общие точки.

38. Если одна из двух параллельных прямых перпендикулярна к третьей, то другая прямая

Перпендикулярна этой прямой

b) Параллельна этой прямой

Скрещивается с этой прямой

d) Не возможно определить.

39. Если две прямые перпендикулярны к плоскости, то они между собой :

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости

Пересекаются под острым углом

Расстояние между параллельными плоскостями в пространстве измеряют по

b) По проекции наклонной

d) Неважно как измерять.

Даны прямая и точка, не лежащая на этой прямой?

Даны прямая и точка, не лежащая на этой прямой.

Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.

(желательно с отрезком).

Выберете верное утверждение : 1 )Если две прямые параллельны одной и то же плоскости , то они параллельны, 2) через точку , лежащую на плоскости, можно провести единственную прямую , перпендикулярную ?

Выберете верное утверждение : 1 )Если две прямые параллельны одной и то же плоскости , то они параллельны, 2) через точку , лежащую на плоскости, можно провести единственную прямую , перпендикулярную данной плоскости, 3)если две различные прямые перпендикулярны одной плоскости , то они параллельны , 4)три несовпадающие плоскости всегда пересекаются по одной прямой или точке.

Даны три точки , не лежащие на одной прямой?

Даны три точки , не лежащие на одной прямой.

Через каждые две точки проведена прямая.

Сколько прямых можно провести?

Перед вами страница с вопросом Даны две параллельные прямые а и б и точка М не лежащая ни на одной из них?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 10 — 11 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

В треугольниках ОА = ОВ как радиусы одной окружности, и О1А = О1В как радиусы другой окружности, сторона ОО1 — общая, треугольники равны по трём сторонам.

В условии допущена ошибка.

1. Где па — мм S = высота проведённая на сторону * сторона, следовательно S = BE * AD, тока на твоём рисунке нифига не понятно по длинам сторон 2. Где треугольник S = высота * 1 / 2 * основание, авс равнобедренный тк оас равнобедренный, во = 5 тк эт..

П о л у ч а е т с я 60 и 120 г р а д у с о в.

KF = ON = 3 TK = KF ; FK + KT = FT = 3 + 3 = 6 ; KO = FN = 7 ; FN = NE ; FN + NE = FE ; 7 + 7 = 14 ; FE = TS = 14 ; TF = SE = 6.

∠AOE = ∠AOB — ∠EOB = 24°.

Исходя из свойств высоты, получаем, что угол АВС равен 30, а катет лежащий на против угла в 30 градусов, равен половине гипотенузы, в данном случае катет это наша высота, следовательно ВС = 3, 45 * 2 = 6, 9.

1)120 2)80 3)60 4)В — 70, С — 40 5)60 6)30 7)40 8) A — 50, C — 70 9)M и К = 50, N — 80 10)Е — 40, D — 60 11)A — 30, D — 90, B — 60 12)A и B — 45, D — 90, M — 90.