Корень из трех на 2 на окружности

Видео:Корень из двух – первая математическая трагедия // Vital MathСкачать

Извлечение корня из комплексного числа

Третий урок по комплексным числам. В этом уроке вы узнаете:

Начнём с ключевого определения.

Видео:Тригонометрическая окружность. Как выучить?Скачать

1. Определение комплексного корня

Определение. Корнем $n$-й степени из комплексного числа $z$, где $nin mathbb $, $n gt 1$, называется такое комплексное число $omega $, что

т.е. $n$-я степень числа $omega $ равна $z$.

Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:

Пример. Вычислить $sqrt[3] $ на множестве комплексных чисел.

Очевидно, привычная нам единица является таким корнем, потому что $ ^ >=-1$. Но есть ещё два корня:

Итого три корня. Как и предполагалось.

Теорема. Для любого комплексного числа $zne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$

Все эти корни считаются по следующей формуле.

Видео:Отбор корней по окружностиСкачать

2. Формула корней

Теорема. Пусть комплексное число записано в тригонометрической форме:

[z=left| z right|cdot left( cos varphi +isin varphi right)]

Тогда все корни степени $n$ из этого числа можно найти по формуле:

По сути, эта теорема является обратной к формуле Муавра:

Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:

1. Перевести комплексное число в тригонометрическую форму;
2. Записать общую формулу корня степени $n$;
3. Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
4. Получим $n$ комплексных корней. Вместе они и будут ответом.

В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $zne 0$.

Представим число $-8i$ в тригонометрической форме:

Запишем формулу корней в общем виде:

[sqrt[3] =2cdot left( cos left( -frac right)+isin left( -frac right) right)=sqrt -i]

В ответе нужно указать все три числа: $-2i$; $sqrt -i$; $-sqrt -i$.

Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $left $, то корни начнут повторяться, и ничего нового мы не получим.

Видео:Как искать точки на тригонометрической окружности.Скачать

3. Геометрическая интерпретация

Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $zne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=sqrt[n] $. Более того: эти точки образуют правильный $n$-угольник.

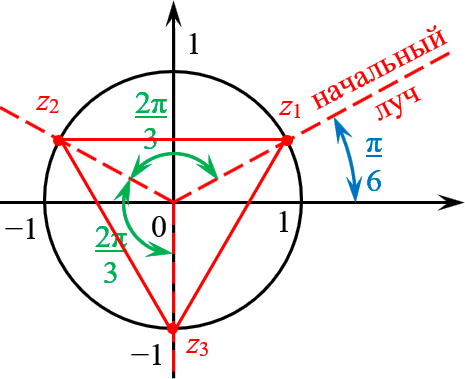
Отметить на комплексной плоскости все числа вида $sqrt[3]$.

Представим число $z=i$ в тригонометрической форме:

Формула комплексных корней:

[sqrt[3] =1cdot left( cos left( frac +frac right)+isin left( frac +frac right) right)]

Это три точки $ _ >$, $ _ >$ и $ _ >$ на окружности радиуса $R=1$:

Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол $ / ;$.

Рассмотрим более сложный пример:

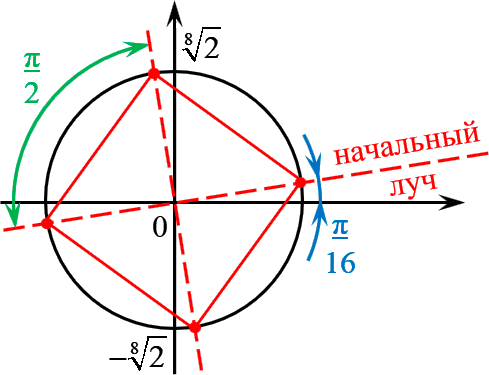
Отметить на комплексной плоскости все числа вида $sqrt[4] $.

Сразу запишем формулу корней с выделением начального луча:

[sqrt[4] =sqrt[8] cdot left( cos left( frac +frac right)+isin left( frac +frac right) right)]

Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=sqrt[8] $, начальный луч $ / ;$:

И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча $ / ;$.

Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:

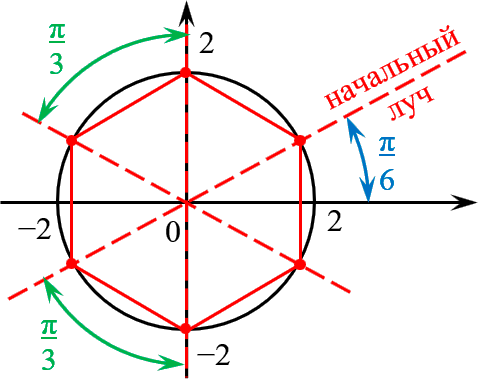
Отметить на комплексной плоскости все числа вида $sqrt[6] $.

Формула корней с выделением начального луча:

[sqrt[6] =2cdot left( cos left( frac +frac right)+isin left( frac +frac right) right)]

Получили правильный шестиугольник со стороной 2 и начальным лучом $ / ;$.

Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $zne 0$:

1. Перевести число в тригонометрическую форму;
2. Найти модуль корня: $sqrt[n] $ — это будет радиусом окружности;
3. Построить начальный луч с отклонением $varphi = / ;$;
4. Построить все остальные лучи с шагом $ / ;$;
5. Получим точки пересечения лучей с окружностью — это и есть искомые корни.

Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $varphi $ — стандартные «табличные» углы вроде $ / ;$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)

Видео:Три способа отбора корней в задании 13 ЕГЭ профильСкачать

4. Почему корней всегда ровно n

С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.

Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:

Последовательно подставим в эту формулу указанные значения параметра $k$:

Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:

Поскольку синус и косинус — периодические функции с периодом $2pi $, $ _ >= _ >$, и далее корни будут повторяться. Как мы и заявляли в самом начале урока.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

5. Выводы

Ключевые факты из урока.

Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $omega $, что $ ^ >=z$.

Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $omega =sqrt[n] $.

Замечание. Если $zne 0$, таких чисел корней будет ровно $n$ штук.

Алгоритм нахождения корней состоит из двух шагов.

Шаг 1. Представить исходное число в тригонометрической форме:

[z=left| z right|cdot left( cos varphi +isin varphi right)]

Шаг 2. Воспользоваться формулой Муавра для вычисления корней:

Все полученные корни лежат на окружности радиуса $sqrt[n] $ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол $ / ;$. Остальные вершины обычно легко находятся из соображений симметрии с помощью циркуля и линейки.

Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».

Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрический круг со всеми значениями, круг синусов и косинусов, линия, ось тангенса на окружности, как пользоваться и находить точки

В каждой профессии существуют свои инструменты, обеспечивающие решение и качественное выполнение определенных задач. Математики применяют тригонометрический круг, позволяющий легко и быстро вычислить значение какой-либо функции. Однако не все могут им правильно пользоваться, поскольку не понимают основных понятий.

Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Общие сведения

Для правильного решения тригонометрических задач следует изучить основные понятия, формулы, а также методы нахождения основных величин. Раздел математики, изучающий функции косинуса, синуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса, называется тригонометрией. Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.

Значения функций, которые можно по ней находить, называются тригонометрическими. Однако существует множество способов нахождения их значений, но в некоторых ситуациях при использовании формул приведения решение затянется на продолжительное время, а вычисления будут громоздкими. Чтобы этого избежать, нужно использовать тригонометрический круг со всеми значениями. С его помощью также можно определить, является ли функция четной или нечетной.

Углы и их классификация

Перед тем как понять основное назначение тригонометрических функций, следует обратить внимание на классификацию углов. Она является важной для вычисления тригонометрических выражений. Углы в математических дисциплинах делятся на следующие типы:

К первому типу относятся углы любой размерности градусной единицы измерения, которая не превышает 90 (а Информация о функциях

Тригонометрических функций всего четыре вида: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существует столько же типов обратных функций: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Они получили широкое применение не только в математических задачах, но также используются в физике, электронике, электротехнике и других дисциплинах. Основной их особенностью считается возможность представления какого-либо закона.

Например, зависимость амплитуды напряжения переменного тока от времени описывается следующим законом: u = Um * cos (w*t) (графиком является косинусоида). Гармонические звуковые колебания также подчиняются определенному закону, в котором присутствует тригонометрическая функция. Кроме того, можно находить значения корня тригонометрического уравнения.

Синусом угла называется величина, равная отношению противолежащего катета прямоугольного треугольника к его гипотенузе. Следовательно, косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение величины противолежащего катета к прилежащему. Котангенс является обратной функцией тангенсу, т. е. отношение прилежащего к противолежащему.

Функции arcsin, arccos, arctg, arcctg применяются в том случае, когда нужно найти значение угла в градусах или радианах. Вычисления выполняются по специальным таблицам Брадиса или с помощью программ. Также можно использовать тригонометрическую окружность.

Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Тригонометрический круг

Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, косинусе, тангенсе, котангенсе, системе координат и теореме Пифагора. Для построения единичной окружности используется декартовая система координат с двумя осями. Точка «О» — центр пересечения координатных осей, ОХ — ось абсцисс, ОУ — ординат.

Для решения задач различного типа применяется и теорема Пифагора. Она справедлива только для прямоугольного треугольника (один из углов — прямой). Ее формулировка следующая: квадрат гипотенузы в произвольном прямоугольном треугольнике равен сумме квадратов катетов. Следует также знать основные соотношения между функциями острых углов в заданном прямоугольном треугольнике:

Существуют и другие тригонометрические тождества, но для работы с кругом этого перечня будет достаточно.

Построение «инструмента»

Построить окружность, которая ускорит процесс решения задач, довольно просто. Для этого потребуются бумага, карандаш, резинка и циркуль. Далее необходимо нарисовать любую немаленькую окружность. После этого отметить ее центр карандашом, поставив точку. Пусть она будет называться «О». Через эту точку следует провести две перпендикулярные прямые (угол пересечения равен 90 градусам). Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).

Окружность является единичной, но не стоит рисовать ее такой, поскольку работать будет неудобно. Этот прием называется масштабированием. Он широко применяется практически во всех сферах человеческой деятельности. Например, инженеры не чертят двигатель космического корабля в натуральную величину, поскольку с таким «рисунком» будет неудобно и невозможно работать. Они используют его макет.

Окружность пересекается с осями декартовой системы координат в 4 точках со следующими координатами: (1;0), (0;1), (-1;0) и (0;-1). Области, которые делят декартовую систему координат на 4 части, называются четвертями. Их четыре:

• Первая состоит из положительных координат по х и у.
• Вторая имеет по х отрицательные и положительные по у.
• Третья — только отрицательные значения.
• Четвертая — положительные значения по х и отрицательные по у.

Исходя из этих особенностей, определяется числовой знак функции, позволяющий определить ее четность и нечетность. Кроме того, на ней следует отметить углы следующим образом: 0 и 2ПИ соответствует точке с координатами (1;0), ПИ/2 — (0;1), ПИ — (-1;0) и 3ПИ/2 — (0;-1).

Готовый макет

Для решения задач специалисты рекомендуют иметь рабочий и готовый макеты тригонометрических окружностей. Первый применяется для нахождения значений нестандартных углов (например, синуса 185 градусов). Тригонометрическим кругом (рис. 1) удобно пользоваться в том случае, когда значение угла является стандартным (90, 60 и т. д.).

Рисунок 1. Готовый макет тригонометрического круга синусов и косинусов.

Для нахождения необходимых значений объединяют две фигуры — единичную окружность и прямоугольный треугольник. Гипотенуза последнего равна 1 и соответствует радиусу окружности. Ось ОХ — косинусы, ОУ — синусы. С помощью этого «инструмента» определение синусов и косинусов становится намного проще. Для нахождения значения sin(30) необходимо воспользоваться следующим алгоритмом:

• Отметить угол на окружности и достроить его до прямоугольного треугольника.
• Если катет лежит напротив угла в 30 градусов, то он равен 0,5 от длины гипотенузы.
• sin(30) = 1 * 0,5 = 0,5.

Для нахождения косинуса необходимо использовать основное тригонометрическое тождество, которое связывает sin и cos: (sin(a))^2 + (cos(a))^2 = 1. Из равенства величина cos(30) = sqrt[1 — (sin(30))^2]= sqrt[1 — 0,5^2] = sqrt(3) / 2.

Однако после всех вычислений следует выбрать знак функции. В данном случае угол находится в первой четверти. Следовательно, функция имеет положительный знак. Для нахождения тангенса и котангенса можно воспользоваться следующими формулами: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a). Подставив значения синуса и косинуса, можно определить значение tg: tg(30) = 0,5 / (sqrt(3) / 2) = 1 / sqrt(3) = sqrt(3) / 3. Тогда котангенс можно найти двумя способами:

• Через известный тангенс: ctg(30) = 1 / (1 / sqrt(3)) = sqrt(3).
• Использовать основное отношение: ctg(30) = (sqrt(3) / 2) / (1/2) = sqrt(3).

Вычислить значения синуса и косинуса для угла 60 градусов очень просто. Для этого нужно воспользоваться основными тождествами: sin(60) = сos(30) = sqrt(3) / 2, cos(60) = sin(30) = 1/2, tg(30) = ctg(60) = sqrt(3) / 3, tg(60) = ctg(30) = sqrt(3). Значения для 45 градусов определяются следующим образом:

• Прямоугольный треугольник с углом 45 градусов является равносторонним (катеты равны).
• (sin(45))^2 + (cos(45))^2 = 1.
• 2 * (sin(45))^2 = 1.
• sin(45) + cos(45) = sqrt(2) / 2.

Тангенс и котангенс равен 1. Если угол равен 90, то необходимо внимательно посмотреть на рисунок 1. Следовательно, sin(90) = 1, cos(90) = 0, tg(90) = 1 и ctg(90) не существует. Линия тангенса на окружности не отображается. В этом случае нужно пользоваться основными тригонометрическими тождествами.

Правила использования

Инструмент позволяет легко и быстро находить значения тригонометрических функций любых углов. Если при решении задачи требуется найти sin(270), то нужно выполнить простые действия:

• Пройти против часовой стрелки (положительное направление) 180 градусов, а затем еще 90.
• На оси синусов значение составляет -1 (точка лежит на оси).

Существуют задачи, в которых угол представлен отрицательным значением. Например, нужно определить синус, косинус, тангенс и котангенс угла (-7ПИ/6). В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).

Пример случая, когда нет необходимости переводить радианы в градусы, является следующим: нужно вычислить значения тригонометрических функций угла 5ПИ/4. Необходимо расписать значение угла таким образом: 5ПИ/4 = ПИ + ПИ/4. Против часовой стрелки следует пройти половину круга (ПИ), а затем его четвертую часть (ПИ/4). Далее нужно спроецировать координаты точки на ось синусов и косинусов. Это соответствует значению sqrt(2)/2. Тангенс и котангенс заданного угла будут равны 1.

Встречаются задачи, в которых значение угла превышает 360 градусов. Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.

Таким образом, тригонометрический круг позволяет оптимизировать вычисления в дисциплинах с физико-математическим уклоном, в которых используются тригонометрические функции. Не имеет смысла устанавливать дополнительное программное обеспечение, пользоваться таблицами, поскольку это занимает некоторое время. При помощи этого «универсального инструмента» можно найти значение любого угла.

Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Видео:Отбор корней по окружностиСкачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Видео:Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

Философская геометрия, Часть 2. Корень из трех и его практическое применение

Сейчас я вам что покажу, закачаетесь. Обязательно загляните под кат, самые интересные картинки я припрятал там.

Я продолжаю рассказ о применении философской геометрии на практике. Прошлая часть была обзорная, она говорила о том, что многие века геометрия использовалась для поиска универсальных идеальных законов природы. Эти законы повсеместно использовались в произведениях искусства, архитектуре и духовной жизни.

Сегодня я расскажу про замечательную пропорцию «корень из трех». Я покажу ее сакральный смысл, а под катом продемонстрирую пример из современного дизайна, который повергнет вас в шок 😉

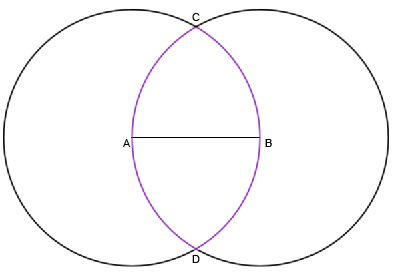
Начнем с построения пропорции. Возьмем отрезок AB.

Примем его за радиус и построим окружность с центром в A.

Теперь построим вторую окружность с тем же радиусом, но с центром в B.

У нас получилась фигура ACBD, имеющая огромное значение для наших предков. Она называется Vescica Piscis (пузырь рыбы). Самый простой и важный пример — она давно является символом христианства.

Я продолжу под катом. Спорим, никогда не догадаетесь чем там все закончится 🙂

Ну вот, раз мы уже под катом, начну сыпать картинки. Мы остановились на Vescica Piscis и символе христианства. Вот Христос вписан в эту фигуру.

Вот здесь изображено много символической рыбы.

Кстати, впервые я про это узнал, купив вот такую подвеску в Кафедральном соборе Уппсалы. Так что символ вполне используется и сейчас.

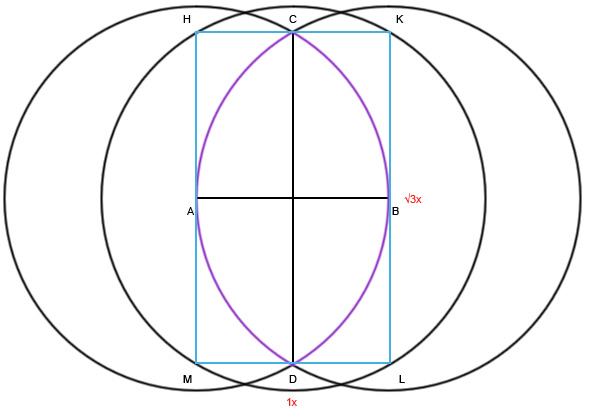
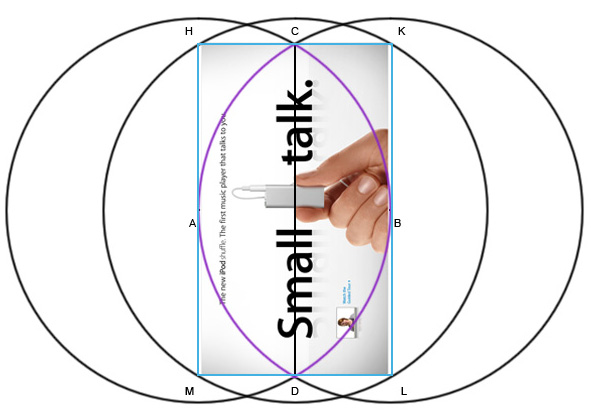
Но чем же так примечательна фигура? Давайте вернемся к построениям. Соединим точки C и D, а из места их пересечения нарисуем еще одну окружность с радиусом AB. Нарисуем прямоугольник HKLM.

Этот прямоугольник обладает замечательным свойством. Его высота относится к ширине ровно как корень их трех (√3 / 1). Корень из трех — это одно из основных иррациональных чисел, но основе которых строилось множество картин, зданий и просто предметов.

Но если вы думаете, что это все старо, уныло и протухло, то вы ошибаетесь. Я обещал сюрприз. Готовы? Только громко не смейтесь.

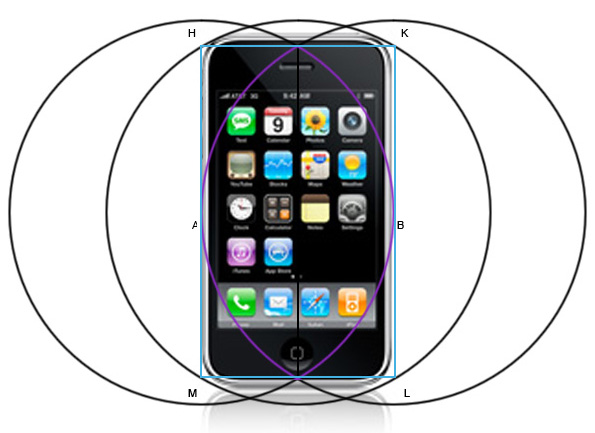
Да-да, это он. iPhone не идеально помещается в этот прямоугольник, но его размеры чрезвычайно близки. Мне кажется что это не совпадение вот почему.
Корень из трех — это примерно 1.732050…
Отношение сторон айфона первого поколения (115×61) примерно равно 1.88524.
iPhone 3G (115.5×61.8) — 1.8599
iPod Touch (110×61.8) — 1.779

Смотрите, они стремятся к идеалу! Мешать им могут только тысячи технических причин.

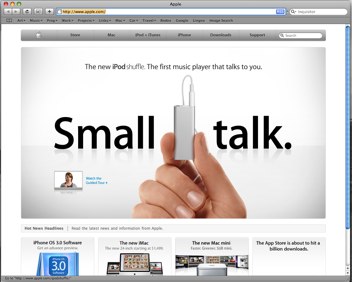
Удивлены? Смущены? Не верите? Сейчас будет больше. Зайдем на apple.com

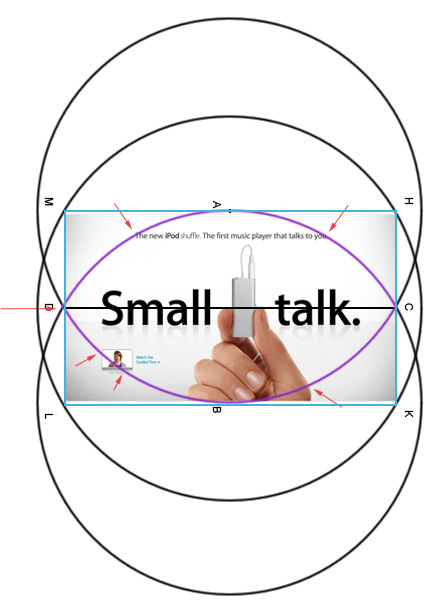
Хм… Что-то мне этот центральный блок напоминает. А ну ка…

Ага! Вот вы и попались. Давайте ка посмотрим поближе.

Обратите внимание как потрясающе дизайны Apple используют эту разметочную сетку. Этому геометрическому построению я даже не знаю сколько сотен лет. Оно использовалось в иконах, храмах, скульптурах. Современные дизайнеры мастерски используют его в обычных коммерческих вещах и оно продолжает безотказно работать. Их вещи покупают вопреки всякому смыслу.

Что же это мистика? Расчет? Геометрия? Философия? Нам остается только практиковаться и пытаться узнать это самим

Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Значения тангенса и котангенса на тригонометрическом круге

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

🔥 Видео

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

Корень из 3 графически.2 СПОСОБ.Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать

Трудный корень из трёхСкачать

3 СПОСОБА ОТБОРА КОРНЕЙ В ЗАДАНИИ #12 (по окружности, неравенством и подбором)Скачать