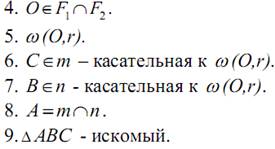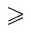Постройте окружности с центрами в вершинах треугольника

§ 23. Метод геометрических мест точек в задачах на построение

Известно, что если смешать синий и жёлтый цвета, то получим зелёный.

Пусть на плоскости надо найти точки, обладающие какими-то двумя свойствами одновременно. Если синим цветом покрасить точки, обладающие первым свойством, а жёлтым — обладающие вторым свойством, то понятно, что зелёные точки будут обладать сразу двумя свойствами. В этом и состоит идея метода ГМТ, которую проиллюстрируем следующими задачами.

Задача 1. Постройте треугольник по трём данным его сторонам.

Решение. Пусть даны три отрезка, длины которых равны a , b , c (рис. 327). Надо построить треугольник ABC , в котором AB = c , AC = b , BC = a .

Проведём произвольную прямую. С помощью циркуля отложим на ней отрезок CB , равный a (рис. 328). Понятно, что задача свелась к построению третьей вершины треугольника, точки A .

Воспользуемся тем, что точка A обладает сразу двумя свойствами:

1) принадлежит геометрическому месту точек, удалённых от точки B на расстояние c , т. е. окружности с центром в точке B радиуса с (см. рис. 328);

2) принадлежит геометрическому месту точек, равноудалённых от точки C на расстояние b , т. е. окружности с центром в точке С радиуса b (см. рис. 328).

В качестве точки A можно выбрать любую из двух образовавшихся зелёных точек.

Полученный треугольник ABC является искомым, так как в нём AB = c , AC = b , BC = a .

Из описанного построения следует, что если каждый из трёх данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.

Задача 2. Постройте фигуру, все точки которой принадлежат данному углу, равноудалены от его сторон и находятся на заданном расстоянии a от его вершины.

Решение. Искомые точки принадлежат сразу двум геометрическим местам точек: биссектрисе данного угла и окружности с центром в его вершине и радиусом, равным a .

Построим биссектрису угла и указанную окружность (рис. 329). Их пересечением является искомая точка X .

Задача 3. Постройте центр окружности радиуса R , проходящей через данную точку M и касающуюся данной прямой a .

Решение. Поскольку окружность касается прямой a , то её центр находится на расстоянии R от этой прямой. Геометрическим местом точек, удалённых от данной прямой на данное расстояние, являются две параллельные прямые (см. упражнение 498). Следовательно, центр окружности находится на прямой b или на прямой с (рис. 330).

Геометрическое место точек, являющихся центрами окружностей радиуса R , проходящих через точку M , — это окружность данного радиуса с центром в точке M . Поэтому в качестве центра искомой окружности можно выбрать любую из точек пересечения окружности с одной из прямых b или с (рис. 331).

Построение для случая, когда данная точка принадлежит данной прямой, рассмотрите самостоятельно.

Задача 4. Постройте треугольник по стороне, медиане, проведённой к этой стороне, и радиусу описанной окружности.

Решение. Построим окружность данного радиуса и проведём хорду AB , равную стороне искомого треугольника. Тогда концы хорды являются двумя вершинами искомого треугольника. Понятно, что третья вершина принадлежит одновременно построенной окружности и окружности с центром в точке O , являющейся серединой хорды AB , и радиусом, равным данной медиане. Каждый из треугольников ABС 1 и ABС 2 (рис. 332) является искомым. Поскольку эти треугольники равны, то задача имеет единственное решение.

622. Даны прямая m и точки A и B вне её (рис. 333). Постройте на прямой m точку, равноудалённую от точек A и B .

623. Точки A и B принадлежат прямой m . Постройте точку, удалённую от прямой m на расстояние a и равноудалённую от точек A и B . Сколько решений имеет задача?

624. Точки B и C принадлежат разным сторонам угла A , причём АВ ≠ АС . Постройте точку M , принадлежащую углу, равноудалённую от его сторон и такую, что MB = MC .

625. Точки B и C принадлежат разным сторонам угла A . Постройте точку D , принадлежащую углу, равноудалённую от его сторон и такую, что DC = BC . Сколько решений может иметь задача?

626. Постройте равнобедренный треугольник по основанию и боковой стороне.

627. Для данной окружности постройте точку, являющуюся её центром.

628. Постройте окружность данного радиуса, проходящую через данную точку, центр которой принадлежит данной прямой.

629. Постройте окружность данного радиуса, проходящую через две данные точки.

630. Найдите все точки, принадлежащие данной окружности и равноудалённые от концов данного отрезка. Сколько решений может иметь задача?

631. Даны две пересекающиеся прямые m и n и отрезок AB . Постройте на прямой m точку, удалённую от прямой n на расстояние AB . Сколько решений имеет задача?

632. В треугольнике ABC известно, что ∠ C = 90°. На катете AC постройте точку D , удалённую от прямой AB на расстояние CD .

633. Постройте равнобедренный треугольник по основанию и радиусу описанной окружности. Сколько решений может иметь задача?

634. Постройте треугольник по двум сторонам и медиане, проведённой к одной из данных сторон.

635. Постройте равнобедренный треугольник по боковой стороне и медиане, проведённой к боковой стороне.

636. На данной окружности постройте точку, находящуюся на данном расстоянии от данной прямой. Сколько решений может иметь задача?

637. На данной окружности постройте точку, равноудалённую от двух данных пересекающихся прямых. Сколько решений может иметь задача?

638. Между двумя параллельными прямыми дана точка. Постройте окружность, проходящую через эту точку и касающуюся данных прямых. Сколько решений имеет задача?

639. Постройте окружность, проходящую через данную точку A и касающуюся данной прямой m в данной точке B .

640. Даны две параллельные прямые и секущая. Постройте окружность, касающуюся этих трёх прямых.

641. Постройте треугольник по двум сторонам и радиусу описанной окружности. Сколько решений может иметь задача?

642. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и радиусу описанной окружности. Сколько решений может иметь задача?

643. Постройте равносторонний треугольник по радиусу описанной окружности.

644. Три прямые попарно пересекаются и не проходят через одну точку. Постройте точку, равноудалённую от всех трёх прямых. Сколько решений имеет задача?

645. Постройте прямоугольный треугольник по катету и сумме гипотенузы и другого катета.

646. Постройте прямоугольный треугольник по гипотенузе и сумме катетов.

647. Постройте прямоугольный треугольник по гипотенузе и разности катетов.

648. Постройте прямоугольный треугольник по катету и разности гипотенузы и другого катета.

649. Постройте равнобедренный треугольник по основанию и разности боковой стороны и высоты, опущенной на основание.

650. Постройте треугольник по стороне, прилежащему к ней углу и сумме двух других сторон.

651. Постройте треугольник по стороне, прилежащему к ней углу и разности двух других сторон.

652. Постройте треугольник по стороне, противолежащему ей углу и разности двух других сторон.

653. Постройте треугольник по стороне, противолежащему ей углу и сумме двух других сторон.

654. Постройте треугольник по стороне, разности углов, прилежащих к этой стороне, и сумме двух других сторон.

655. Постройте треугольник по периметру и двум углам.

656. Постройте остроугольный треугольник по периметру, одному из углов и высоте, проведённой из вершины другого угла.

657. Постройте треугольник по высоте и медиане, проведённым из одной вершины, и радиусу описанной окружности.

658. Постройте треугольник по двум сторонам и медиане, проведённой к третьей стороне.

659. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и медиане, проведённой к одной из двух других сторон.

Упражнения для повторения

660. На рисунке 334 ∠ A = 46°, ∠ ACB = 68°, ∠ DEC = 120°. Найдите углы треугольников EFC и DBE .

661. Через середину O стороны MK треугольника MKN провели прямую, перпендикулярную стороне MK и пересекающую сторону MN в точке C . Известно, что MC = KN , ∠ N = 50°. Найдите угол MCO .

662. В треугольнике ABC из вершины прямого угла C провели высоту CH и биссектрису CM . Длина отрезка HM в 2 раза меньше длины отрезка CM . Найдите острые углы треугольника ABC .

663. На рисунке 335 BD = DC , DN ⊥ BC , ∠ BDM = ∠ MDA . Найдите сумму углов MBN и BMD .

Наблюдайте, рисуйте, конструируйте, фантазируйте

664. Разрежьте фигуру, изображённую на рисунке 336, на три части, не являющиеся квадратами, так, чтобы из этих частей можно было сложить квадрат.

Когда сделаны уроки

Из истории геометрических построений

Умение достигать результат, используя минимальные средства, всегда считалось признаком высокого мастерства. Видимо, поэтому в Древней Греции в значительной степени было развито искусство выполнять геометрические построения с помощью только двух инструментов: дощечки с ровным краем (линейки) и двух заострённых палочек, связанных на одном конце (циркуля). Такое ограничение в выборе инструментов историки связывают с древнегреческой традицией, считавшей прямую и окружность самыми гармоничными фигурами. Так, в своей книге «Начала» великий учёный Евклид описывал построения геометрических фигур, при которых использовались лишь циркуль и линейка.

Существует много задач на построение. С некоторыми из них вы уже успели познакомиться. Однако есть три задачи на построение, которые сыграли в развитии математики особую роль. Эти задачи стали знаменитыми.

Задача о квадратуре круга. Построить квадрат, площадь которого равна площади данного круга.

Задача о трисекции угла (от латинских tria — «три» и section — «разрезание») . Разделить угол на три равные части.

Задача об удвоении куба. Построить куб, объём которого в 2 раза больше объёма данного куба.

Эти задачи занимали умы людей на протяжении тысячелетий. Их пытались решить и такие выдающиеся учёные древности, как Гиппократ Хиосский, Евдокс Книдский, Евклид, Эратосфен, Аполлоний Пергский, Герон, Папп, Платон, Архимед, и гении Нового времени Рене Декарт, Франсуа Виет, Исаак Ньютон. И лишь в середине XIX века была доказана их неразрешимость, т. е. невозможность выполнить указанные построения с использованием лишь циркуля и линейки. Этот результат был получен средствами не геометрии, а алгебры, благодаря переводу этих задач на язык уравнений.

Когда вы решали задачи на построение, особенно те, которые отмечены знаком , вы, по-видимому, испытали сложности, связанные с ограниченностью набора инструментов. Поэтому предложение ещё больше сузить возможности применяемых приборов может показаться вам по меньшей мере неожиданным. Однако ещё в Х веке персидский математик Мохаммед Абу-ль-Вефа описал решение целого ряда задач на построение с помощью линейки и циркуля, раствор которого нельзя было менять. Совсем удивительной является теорема, опубликованная в 1797 году итальянским математиком Лоренцо Маскерони (1750–1800): всякое построение, выполнимое циркулем и линейкой, можно проделать одним циркулем. При этом Маскерони обусловливал следующее: поскольку одним циркулем провести прямую нельзя, то прямая считается построенной, если построены какие-нибудь две её точки.

В ХХ веке была обнаружена книга датского учёного Георга Мора (1640–1697), в которой он также описал построения одним циркулем. Поэтому сформулированную выше теорему называют теоремой Мора — Маскерони.

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Примеры решения задач, решаемых методом ГМТ

Задача 1. На стороне треугольника найти точку, равноотстоящую от двух

других сторон треугольника.

Анализ. Пусть задача решена и точка М на стороне АВ находится на

одинаковом расстоянии от сторон АС и ВС, образующих угол С.

Так как все точки, равноудаленные от сторон угла С лежат на биссектрисе этого угла (гмт 5), то точка М удовлетворяет двум независимым условиям:

Доказательство. Легко видеть, что точка М удовлетворяет требованиям

Задача 2. Построить треугольник по основанию а, углу при вершине А

Анализ. Допустим, что задача решена и искомый треугольник ΔАВС

построен так, что BC = a, AM = m_а – медиана и ∟ВАС = α.

Отрезок ВС, равный данному, всегда может быть построен. Тогда задача сводится к построению точки А, удовлетворяющей двум независимым условиям:

1 0 . Точка А находится на расстоянии m_а от середины М стороны ВС, т.е.

2 0 . Так как ∟ВАС = α, то точка А принадлежит ГМТ F1, из которых отрезок ВС виден под углом α, т.е.

Таким образом,

Заданные по условию задачи элементы могут быть выбраны перед построением или анализом.

Доказательство: BC = a, AM = m_а по построению, и ∟СВО = 90 0 – α, следовательно, ∟ВОМ = α, следовательно, ∟ВОС=2α, а ∟ВАС =0,5*∟ВОС= α

и, следовательно ΔАВС, удовлетворяет всем условиям задачи и потому искомый.

Исследование: Задача имеет столько решений, сколько точек содержит

пересечение двух окружностей. Если пересечение в двух точках, то два

решения; в одной (окружности касаются) – одно решение, не пересекаются –нет решений.

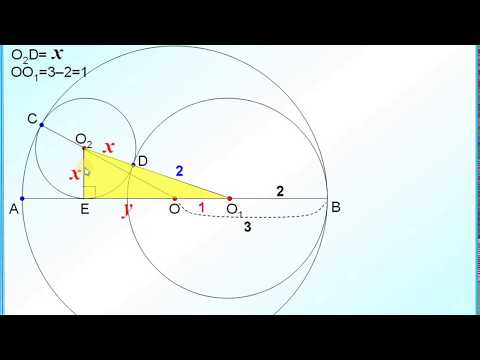
Задача 3. Построить окружность данного радиуса r, проходящую через данную точку М и высекающую на данной прямой l отрезок длины d, равный данному.

Анализ: Пусть искомая окружность построена. Пусть О – ее центр, r – данный радиус, М – данная точка, АВ – хорда длины d, построенной окружности, лежащей на данной прямой l. Опустим перпендикуляр ОC на прямую l. В прямоугольном треугольнике ОВС известна гипотенуза (данный радиус r) и катет ВС, равный половине данного отрезка. Кроме того, ОМ = r.

Значит, искомый центр О принадлежит, во-первых ГМТ F1, удаленных от данной прямой l на расстояние, равное ОС(ГМТ 3); во-вторых ГМТ F2, удаленных от данной точки М на расстояние, равное данному радиусу r (гмт2).

Окружность ω может быть построена, ГМТ F1 может быть построено, если мы найдем расстояние OC = h.

Для этого построим вспомогательный треугольник О₁В₁С₁ по гипотенузе О₁В₁ = r и катету В₁С₁ = d/2. Тогда h = O₁C₁ будет найден.

Построение:

Доказательство: Убеждаемся в том, что построенная окружность удовлетворяет всем требованиям задачи. OM = r по построению. Докажем, что AB = d.

Действительно, ΔАОВ — равнобедренный (ОС –

медиана и высота), отсюда АВ = 2ВС = 2*d/2 = d.

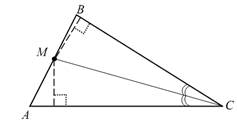
Исследование: Построение 1 возможно, если d 0 ) точки О можно отметить сразу – она находится на расстоянии r от стороны ВС, то есть центр О вписанной окружности принадлежит ГМТ, находящихся на расстоянии r от прямой ВС (ГМТ 3). (Как правило, мы строим только в одной из двух полуплоскостей, определяемых заданной прямой). Второе свойство, которым обладает точка О, видно не сразу. Но, исходя из свойств вписанной окружности, это свойство мы можем найти: центр вписанной окружности находится на пересечении биссектрис треугольника и потому ОВ и ОС – биссектрисы углов В и С.

Тогда: ∟ВОС = 180 0 – 0,5(∟В + ∟С) = 180 0 – 0,5 (180 0 — ∟А) = 90 0 + 0,5∟А

Так как ∟ВОС =90 0 +∟A/2, то точка О принадлежит ГМТ F2, из которых

данный отрезок ВС виден под данным углом α = 90 0 + ∟А/2 (ГМТ 6). ГМТ F1 и F2 может быть построено, а потому и точка может быть построена и мы можем перейти к построению искомой фигуры.

Доказательство: Убеждаемся в том, что построенный треугольник

удовлетворяет всем требованиям задачи. ВС = а, окружность ω(O,r) вписана в

треугольник по построению. Остается доказать, что ∟ВАС равен данному углу

А. Действительно, по построению ∟О₁ ВК = ∟А/2. Тогда

Теперь находим:

Значит, ΔАВС удовлетворяет всем условиям задачи, а потому – искомый.

Исследование. Построения 1-3 выполняются и притом однозначно при

любых a, r и ∟ A 0 . Построение 4 возможно лишь тогда, когда прямая F1

пересекает окружность F2, то есть при условии или при: (*). При этом прямая F1 пересекает окружность F2 в

двух или одной точке соответственно. Построения 6 и 7 всегда выполнимы, так

как из любой точки вне окружности можно провести к ней две касательные

(одна из них в данном случае прямая ВС). А вот построение 8 возможно не всегда: прямые m и n могут быть параллельными или могут пересекаться в полуплоскости, не содержащей точку О. В этих случаях в нужной нам полуплоскости точка А не строится. Вывод: при выполнении условий ∟A 0 и (*) задача может иметь одно, два или ни одного решения.

4. Построение Штейнера и построение с помощью
двусторонней линейки, прямого или острого угла [2], [5]

Якоб Штейнер (18.05 1795г. – 01.04.1863г.) сын простых поселян из Уцисдорфа Германии. Как он сам писал: «Только на девятнадцатом году стремление к образованию стало для меня потребностью…. и с осени 1822г. Вынужден с величайшим трудом добывать средства к существованию частными уроками. Почти бессознательно я пришел таким образом к собственно геометрическому способу рассмотренья, как оно должно быть присуще геметрии древности, но я находился в случае, противоположном им. Мне было дано множество разрешимых задач и предложений, и мне приходилось заняться не фиксацией отдельных предложений, а установлением того свойства общих законов систематического построения, что из них вытекают все открытия подобного рода, и их соответственным образом исчерпать».

«Геометрия в более тесном смысле для своих построений нуждается только в двух инструментах, циркуле и линейке. …. все построения могут быть выполнены только при помощи линейки, если где-либо в дан будет вспомогательный неподвижный круг»

Рассмотрим решение задач проведением только одних прямых линий, причём на чертеже иногда уже имеется начерченной какая-нибудь одна вспомогательная фигура. Из всех таких способов наиболее сильными являются решения с помощью:

1. Двусторонней линейки, другие инструменты при этом не допускаются

2. Прямого или острого угла, сделанного из дерева или металла — другие инструменты не допускаются.

3. Односторонней линейки, причём на чертеже уже имеется начерченной окружность с известным центром.

Далее, всякая не вспомогательная окружность считается данной, если известно положение ее центра и длина радиуса, заданная где-нибудь начерченным отрезком. Однако ни одна точка такой окружности точку какого-нибудь свойства, то должны ограничиться проведением только прямых линий.

Мы знаем, что решение квадратной задачи сводится к известным четырём основным построениям.

Из этих основных задач первая и третья решаются способами 1, 2 и 3

непосредственно — одной линейкой. Моя цель показать, что две другие основные задачи решаются теми же тремя способами, которые решают теми же способами всякую квадратную задачу.

Решим несколько задач проведением одних прямых линий (односторонней линейкой).

Найти геометрическое место центров окружностей, проходящих через две данные точки.

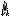
Пусть окружность с центром O проходит через данные точки A и B. Поскольку OA = OB (как радиусы одной окружности), точка O лежит на серединном перпендикуляре к отрезку AB. Обратно, каждая точка O, лежащая на серединном перпендикуляре к AB, равноудалена от точек A и B. Значит, точка O — центр окружности, проходящей через точки A и B.

Проведем диаметры АА1, ВВ1, затем хорды АВ1, ВА1, эти последние перпендикулярны АВ и потому параллельны между собой. Поэтому для решения задачи нужно провести через точку О прямую, параллельную эти хордам. Она будет серединным перпендикуляром к АВ, т.е. искомым ГМТ [5, стр.21]

Дан прямоугольник ABCD. Найдите ГМТ X, для которых AX + BX = CX + DX.

Пусть l — прямая, проходящая через середины сторон BC и AD.

Предположим, что точка X не лежит на прямой l, например, что точки A и X лежат по одну сторону от прямой l. Тогда AX

Видео:Построить описанную окружность (Задача 1)Скачать

Задачи на построение циркулем и линейкой с примерами решения

Содержание:

Основные задачи на построение циркулем и линейкой:

В данном параграфе рассмотрим вопрос о построении геометрических фигур. Вы уже знаете, что геометрические построения можно осуществлять с помощью масштабной линейки, циркуля, транспортира и чертежного угольника. В то же время оказывается, что многие геометрические фигуры можно построить, пользуясь только циркулем и линейкой без масштабных делений.

При построении геометрических фигур с помощью циркуля и линейки без масштабных делений учитывается, что:

1. с помощью линейки можно провести произвольную прямую, а также построить прямую, проходящую через две точки;
2. с помощью циркуля можно провести окружность произвольного радиуса, а также построить окружность с центром в данной точке и радиусом, равным данному отрезку.

Теперь рассмотрим основные задачи на построение циркулем и линейкой: построение угла, равного данному, построение серединного перпендикуляра к отрезку, построение биссектрисы угла.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Задача 1 (построение угла, равного данному)

От данного луча OF отложите угол, равный данному углу ABC.

Предположим, что угол DOF, удовлетворяющий условию задачи, построен (рис. 130, а).

Пусть

1) Строим окружность (В, R) , где R — произвольный радиус, и отмечаем точки А₁ и С₁ пересечения ее со сторонами угла ABC.

2) Строим окружность 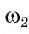(0, R) с центром в точке О того же радиуса R и отмечаем ее точку пересечения F₁ с лучом OF.

3) Строим окружность (F₁, A₁C₁).

4) Пусть D₁ — одна из точек пересечения окружностей 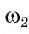(0, R) и (F₁, A₁C₁) (рис. 130, б). Тогда угол D₁OF — искомый. Докажем, что D₁OF =ABC.

Равенство D₁OF =ABC следует из равенства треугольников А₁ВС₁ и D₁OF₁. Действительно, по построению А₁В = D₁O = С₁В = F₁O. Кроме того, по построению F₁D₁ = А₁С₁, следовательно, треугольники А₁ВС₁ и D₁OF₁ равны по трем сторонам. Отсюда следует, что D₁OF =А₁ВС₁, т. е. построенный угол D₁OF равен данному углу ABC.

Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Задача 2 (построение серединного перпендикуляра к отрезку)

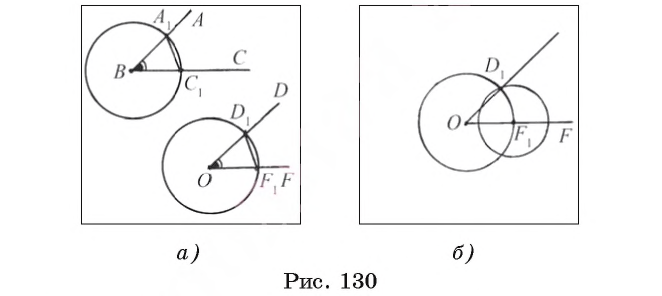
Постройте серединный перпендикуляр к данному отрезку АВ.

Проведем рассуждения, которые помогут осуществить необходимое построение. Предположим, что серединный перпендикуляр а к отрезку АВ построен (рис. 131, а). Пусть точки F и D лежат на серединном перпендикуляре так, что OF = OD. Прямоугольные треугольники FOB и DOB равны по двум катетам, следовательно, BF = BD. Иначе говоря, точки F и D лежат на окружности (B, BF) и BF > ОВ. Аналогично AF =AD, так как треугольник FOA равен треугольнику DOA. Кроме того, легко увидеть, что AF = BF. Таким образом, точки F и D лежат также и на окружности (A, BF).

1) Строим окружности (A, R) и (B, R) , где R AВ. Пусть, например, R = AB: (A, AB) и (B, AB) (рис. 131, б).

2) Отмечаем точки F и D пересечения окружностей (A, AB) и (B, AB).

3) Тогда прямая FD — серединный перпендикуляр к отрезку АВ. Докажем это.

Рассмотрим треугольники FAD и FBD (рис. 131, в). Указанные треугольники равны по трем сторонам. Следовательно, AFD = BFD. Отсюда следует, что в равнобедренном треугольнике AFD отрезок FO является биссектрисой, а значит, и высотой и медианой, т. е. прямая FO — серединный перпендикуляр к отрезку АВ.

Видео:Как построить окружность, описанную около треугольника, в программе ГЕОГЕБРАСкачать

Задача 3 (построение биссектрисы угла)

Постройте биссектрису данного угла ABC.

Допустим, что биссектриса BE данного угла ABC построена (рис. 132, а). Пусть точки F и D лежат на сторонах угла так, что BF = BD, О = FD BE, а точка Т лежит на луче, противоположном лучу ОВ. Из равенства прямоугольных треугольников FOT и DOT (FO = OD, катет ОТ — общий) следует, что FT = DT, т. е. точка Т принадлежит окружностям равных радиусов с центрами в точках F и D. Построив точку Т, мы построим биссектрису ВТ данного угла.

1) Строим окружность (B, R₁) произвольного радиуса R₁ с центром в вершине В данного угла (рис. 132, б).

2) Отмечаем точки F и D, в которых окружность (B, R) пересекает соответственно стороны ВА и ВС данного угла.

3) Строим окружности (F, R₂) и (D, R₂), где R2 > FD. Отмечаем точку Т их пересечения, которая лежит внутри данного угла.

4) Проводим луч ВТ. Луч ВТ — искомый. Докажем это.

Рассмотрим треугольники BFT и BDT (рис. 132, в). Эти треугольники равны по трем сторонам (BF = BD и FT = DT — по построению, ВТ — общая сторона). Из равенства этих треугольников следует, что FBT = DBT, т. е. луч ВТ — биссектриса угла ABC.

Видео:ЕГЭ Задание 16 Три окружностиСкачать

Построение треугольника по трем элементам

В данном пункте рассмотрим задачи на построение треугольника по: а) двум сторонам, и углу между ними; б) стороне и двум прилежащим к ней углам; в) трем сторонам.

Видео:Строим треугольник по стороне, медиане и радиусу описанной окружности (Задача 8).Скачать

Задача 4 (построение треугольника по двум сторонам и углу между ними)

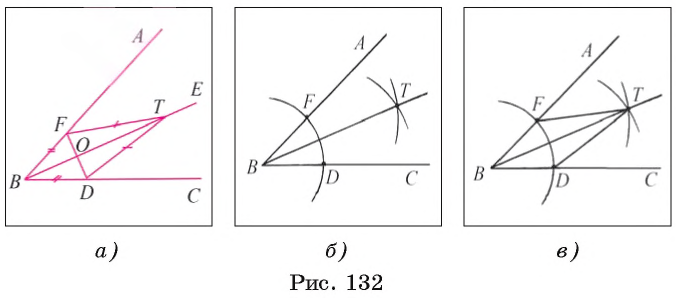
Постройте треугольник, две стороны которого равны двум данным отрезкам а и b, а угол между этими сторонами равен данному углу hk.

Даны два отрезка а, b и угол hk (рис. 133, а). Требуется с помощью циркуля и линейки построить треугольник ABC, две стороны которого, например, АВ и АС, равны соответственно отрезкам а и b, а угол ВАС равен углу hk.

1) Проведем прямую, на ней отложим отрезок АС, равный отрезку b (рис. 133, б).

2) Строим угол CAF, равный углу hk.

3) На луче AF отложим отрезок АВ, равный отрезку а, и проведем отрезок ВС. Треугольник ABC — искомый (рис. 133, в).

По построению имеем, что АС = b, АВ = а и BAC = hk.

При любых данных отрезках а и b и неразвернутом угле hk каждое из построений 1) — 3) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по двум сторонам и углу между ними, поэтому говорят, что данная за дача имеет единственное решение.

Видео:Задача по темам: окружность, равнобедренный треугольник. "Окружности с центрами в точках Р и Q ..."Скачать

Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)

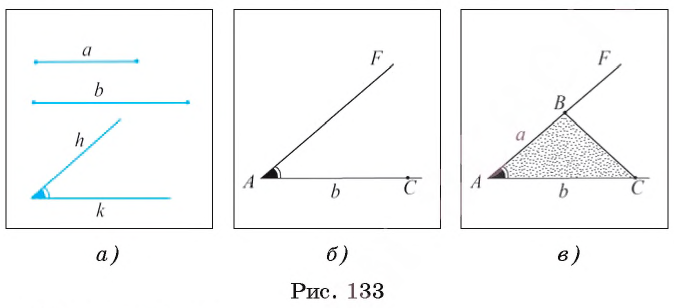
Постройте треугольник, сторона которого равна данному отрезку а, а углы, прилежащие к этой стороне, равны данным углам hk и mq.

Дан отрезок а и два угла hk и mq (рис. 134, а). Требуется с помощью циркуля и линейки построить треугольник ABC, сторона которого, например АС, равна отрезку а, а углы ВАС и ВСА равны соответственно углам hk и mq.

1) Проведем прямую и на ней отложим с помощью циркуля отрезок АС, равный отрезку а (рис. 134, б).

2) Строим угол CAF, равный углу hk.

3) Строим угол ACT, равный углу mq.

4) Отмечаем точку В пересечения лучей AF и СТ. Треугольник ABC — искомый (рис. 134, в).

По построению имеем, что АС = a, BAC = hk и ACB = mq.

Для любого данного отрезка а и неразвернутых углов hk и mq каждое из построений 1) — 4) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по стороне и двум прилежащим к ней углам, поэтому говорят, что данная задача имеет единственное решение.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Задача 6 (построение треугольника по трем сторонам)

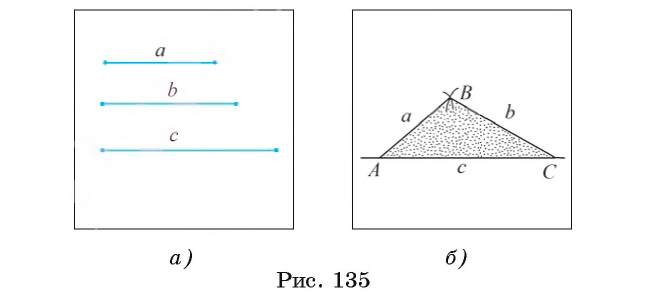
Постройте треугольник, стороны которого равны данным отрезкам а, b, с.

Даны отрезки а, b, с (рис. 135, а). Требуется с помощью циркуля и линейки построить треугольник ABC, стороны которого АВ, ВС и АС равны соответственно отрезкам a, b и с.

1) Проведем прямую и на ней с помощью циркуля отложим отрезок АС, равный отрезку с (рис. 135, б).

2) Строим окружность (A, a).

3) Строим окружность (C, b).

4) Пусть В — одна из точек пересечения окружностей (A, a) и (C, b). Тогда треугольник ABC — искомый.

По построению АС = с, АВ = а, ВС = b.

Данная задача не всегда имеет решение. Известно, что в любом треугольнике длина каждой стороны меньше суммы длин двух других его сторон. Таким образом, если длина какого-либо из данных отрезков больше суммы длин двух других, то нельзя построить треугольник, стороны которого равны данным отрезкам.

• Задачи на построение по геометрии
• Угол — определение, виды, как обозначают с примерами
• Перпендикулярные прямые в геометрии
• Признаки равенства треугольников
• Соотношения между сторонами и углами треугольника
• Неравенство треугольника — определение и вычисление
• Свойства прямоугольного треугольника
• Расстояние между параллельными прямыми

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🔍 Видео

16 задание ОГЭ 2023 Окружность Треугольник #Shorts #огэпоматематике2023 #геометрия #окружностьСкачать

Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Построить окружность, описанную около треугольникаСкачать

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Центр окружности описанной вокруг треугольникаСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Построение окружности по трём точкам.Скачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия. 7 класс. Урок 9 "Окружность проходящая через вершины треугольника"Скачать