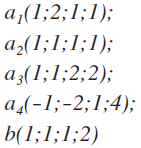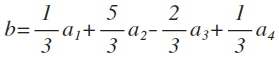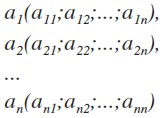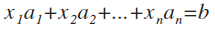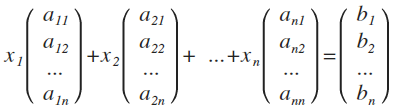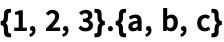Найти базис векторов в вольфраме (4 видео)

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Содержание

Разложение вектора по базису в Wolfram|Alpha
Векторный анализ и визуализация
Базис системы векторов: онлайн-калькулятор
Материалы, которые помогут вам лучше разобраться в теме:
Как найти базис векторов онлайн
📹 Видео

Разложение вектора по базису в Wolfram|Alpha

Как разложить вектор b по базису a1, a2, a3, a4? Рассмотрим на примере.

Пусть даны векторы:

Чтобы разложить вектор b по базису a1, a2, a3, a4 выполним запрос:

Таким образом, разложение вектора b по базису a1, a2, a3, a4 имеет вид:

Далее, для самых любознательных, приводится краткое обоснование этого способа.

Базисом n-мерного пространства служит любая система n линейно независимых n-мерных векторов.

Ранее уже рассмотрена линейная зависимость векторов в Wolfram|Alpha, и было показано, как с помощью Wolfram|Alpha можно проверить, являются ли данные векторы линейно независимыми.

Задача «разложить, вектор b по базисным векторам a1, a2 . an», означает — выразить вектор b через базисные векторы a1, a2, . an, то есть — найти коэффициенты x1, x2. xn, при которых линейная комбинация векторов a1, a2, . an равна вектору b:

Коэффициенты x1, x2. xn этого разложения (этой линейной комбинации) являются координатами вектора b в базисе a1, a2, . an.

Указанное векторное уравнение можно представить в координатной форме:

В свою очередь, это уравнение эквивалентно следующей системе линейных алгебраических уравнений, в которой координаты вектора b в базисе a1, a2, . an в базисе являются неизвестными:

Видео:Как разложить вектор по базису - bezbotvyСкачать

Векторный анализ и визуализация

В Языке Wolfram n-мерные вектора представляются в виде списков длиной n.

Out[1]=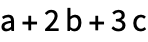

Для расчета векторного произведения необходимо ввести символ ESC cross ESC :

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Базис системы векторов: онлайн-калькулятор

Векторы, образующие базис, являются линейно независимыми. В противном случае решения нет. Алгоритм в основе калькулятора проверяет соблюдение этого условия. При положительном результате переходит к дальнейшим расчетам.

Доказать, что векторы образуют базис, понадобится при решении задач по аналитической геометрии и выполнении типовых заданий по алгебре. Используйте наш сервис для отработки теорем и правил необходимое количество раз. Вы получите ответ с подробным решением любой задачи бесплатно.

Задайте размерность вектора. Цифра меняется с помощью кнопок «+», «-».
Введите значения базисных векторов в соответствующие окна. Отправьте задание на вычисление кнопкой «Рассчитать».
Способ решения содержит векторное уравнение, которое преобразовывается в матричный вид для решения методом Гаусса. Кнопкой «Показать подробное решение» вы можете развернуть последовательные вычисления.
После вычислений доступен ответ.

Видео:Найдите разложение вектора по векторам (базису)Скачать

Материалы, которые помогут вам лучше разобраться в теме:

Видео:Образуют ли данные векторы базисСкачать

Как найти базис векторов онлайн

Автоматические расчеты производятся по проверенным формулам и тестируются на примерах. Поэтому с помощью онлайн-калькулятора вы сможете получить точный ответ.

Показать, что векторы образуют базис, несложно. Для этого необходимо:

Найти определитель, построенный на данных векторах. Его значение не должно быть равным нулю.
Произвести дальнейшие вычисления по методу Гаусса.

Раздел онлайн-калькуляторов охватывает не только тему векторов. Здесь собраны все основные типы задач. Сервисом часто пользуются студенты технических специальностей. Также среди нашей аудитории – школьники, их родители, преподаватели, ученые, работники конструкторских бюро и др.

Теперь подготовка к занятиям стала быстрой и доступной. Вы можете сверить ответы и найти у себя ошибку, изучив полученное решение. После нескольких тренировок способ вычислений становится понятным, его можно применять на самостоятельных, семинарах, зачетах.

Мы разработали понятный интерфейс для удобного использования. Если остались вопросы, смотрите инструкцию. Для индивидуального объяснения непонятной темы напишите консультанту и получите скидку на первое занятие с преподавателем.