- Источник задания: Решение 4351. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.
- Дан выпуклый четырехугольник известно что а найти
- Дан выпуклый четырехугольник известно что а найти
- Разделы
- Дополнительно
- Задача по математике — 6838
- Задача по математике — 6839
- Задача по математике — 6840
- Задача по математике — 6841
- Задача по математике — 6842
- Задача по математике — 6843
- Задача по математике — 6844
- Задача по математике — 6845
- Задача по математике — 6846
- Задача по математике — 6847
- Задача по математике — 6848
- Задача по математике — 6849
- Задача по математике — 6850
- Задача по математике — 6851
- Задача по математике — 6852
- 🔥 Видео
Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Источник задания: Решение 4351. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.
Задание 16. Дан выпуклый четырёхугольник ABCD со сторонами АВ = 5, ВС = CD = 3, AD = 8 и диагональю АС = 7.
а) Докажите, что около него можно описать окружность.
б) Найдите диагональ BD.
а) Если вокруг четырехугольника можно описать окружность, то сумма его противоположных углов будет равна 180 градусов. Это необходимое и достаточное условие для доказательства этого положения. Докажем, что сумма углов 

Аналогично для угла 
Таким образом получаем, что

то есть вокруг данного четырехугольника можно описать окружность.
б) Рассмотрим треугольник ABD и по теореме косинусов можно записать:
Также диагональ BD можно вычислить по теореме косинусов из треугольника BCD:
Вычтем (1) и (2), получим:
Подставим это значение в (2), найдем BD:

Ответ: 
Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Дан выпуклый четырехугольник известно что а найти
В выпуклом четырёхугольнике ABCD известно, что AB = BC, AD = CD, ∠B = 32°, ∠D = 94°. Найдите угол A. Ответ дайте в градусах.
Проведем диагональ АС, получим два треугольника BAC и CAD. Рассмотрим треугольник ВАС, равнобедренный: угол ВАС = ∠BCA = x, получим уравнение:
Рассмотрим равнобедренный треугольник ACD, угол ACD = ∠CAD = у, составим уравнение:
Угол А равен сумме углов ВАС и CAD = 74 + 43 = 117.
Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

Дан выпуклый четырехугольник известно что а найти
Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Разделы 
Видео:9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

Дополнительно
Задача по математике — 6838
Дан треугольник со сторонами 25, 25 и 48.
а) Докажите, что он тупоугольный.
б) Найдите расстояние между центрами его вписанной и описанной окружностей.
Задача по математике — 6839
Длины сторон $AB$, $AD$, $BC$ и $CD$ выпуклого четырёхугольника $ABCD$ в указанном порядке образуют арифметическую прогрессию.
а) Докажите, что в этот четырёхугольник можно вписать окружность.
б) Найдите радиус этой окружности, если известно, что $AB=6$, $AD=8$, $BC=10$, $CD=12$ и $BD=BC$.
Задача по математике — 6840
Дан выпуклый четырёхугольник $ABCD$ со сторонами $AB=3$, $BC=CD=5$, $AD=8$ и диагональю $AC=7$.
а) Докажите, что около него можно описать окружность.
б) Найдите диагональ $BD$.
Задача по математике — 6841
Сторона $AC$ треугольника $ABC$ больше стороны $AB$. Вписанная в треугольник окружность касается стороны $BC$ в точке $M$, а вневписанная — в точке $N$.
а) Докажите, что $MN=AC-AB$.
б) Найдите расстояние между центрами указанных окружностей, если сумма их радиусов равна 24, а $MN=10$.
Задача по математике — 6842
Диагонали $AC$ и $BD$ выпуклого четырёхугольника $ABCD$ перпендикулярны.
а) Докажите, что $AB^+CD^=BC^+AD^$.
б) Известно, что в этот четырёхугольник можно вписать окружность. Найдите её радиус, если $BC=8$, $CD=12$, $angle BAD=150^$.
Задача по математике — 6843
Точка $M$ — середина гипотенузы $AB$ прямоугольного треугольника $ABC$. На отрезке $CM$ как на диаметре построена окружность.
а) Докажите, что она проходит через середины катетов.
б) $AP$ и $BQ$ — касательные к этой окружности ($P$ и $Q$ — точки касания). Найдите отношение $AP:BQ$, если известно, что $tgangle ABC=2$.
Задача по математике — 6844
Четырёхугольник $ABCD$ с перпендикулярными диагоналями $AC$ и $BD$ вписан в окружность.
а) Докажите, что прямая, проходящая через точку пересечения диагоналей четырёхугольника перпендикулярно стороне $BC$, делит пополам сторону $AD$.
б) Найдите стороны четырёхугольника $ABCD$, если известно, что $AC=84$, $BD=77$, а диаметр окружности равен 85.
Задача по математике — 6845
Отрезок $CD$ — биссектриса треугольника $ABC$. Окружность, проходящая через точки $C$ и $D$ касается стороны $AB$ и пересекает стороны $AC$ и $BC$ в точках $M$ и $N$ соответственно.
а) Докажите, что $MNparallel AB$.
б) Найдите $MN$, если известно, что $AD=2$, $BD=4$ и $AM=1$.
Задача по математике — 6846
Основание и боковая сторона равнобедренного треугольника равны 26 и 38 соответственно.
а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.
б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.
Задача по математике — 6847
В окружность вписан четырёхугольник с тремя равными сторонами.
а) Докажите, что в этом четырёхугольнике есть параллельные стороны.
б) Найдите диагонали четырёхугольника, если известно, что радиус окружности равен 25, а каждая из трёх равных сторон четырёхугольника равна 30.
Задача по математике — 6848
В выпуклом четырёхугольнике $ABCD$ известно, что $cosangle ABC=-cosangle ADC$.
а) Докажите, что $angle ABD=angle ACD$.
б) Найдите радиус окружности, описанной около этого четырёхугольника, если известно, что $angle ACB=30^$, $BC=6$, а высоты треугольников $ABD$ и $CBD$, проведённые из вершины $B$, равны.
Задача по математике — 6849
Окружность с центром $O$, вписанная в треугольник $ABC$, касается сторон $AB$ и $AC$ в точках $M$ и $N$ соответственно, $AH$ — высота треугольника. Прямые $MN$ и $BC$ пересекаются в точке $K$.
а) Докажите, что $angle MKB=angle OAH$.
б) Найдите $AK$, если известно, что $angle ABC=77^$, $angle ACB=17^$, а отрезок, соединяющий точку $H$ с серединой $MN$, равен 8.
Задача по математике — 6850
На основаниях $AD$ и $BC$ трапеции $ABCD$ построены квадраты $ADEF$ и $BCGH$, расположенные вне трапеции.
а) Докажите, что прямая $FG$ проходит через точку пересечения диагоналей трапеции.
б) Прямая, проходящая через центры квадратов, пересекает основание $BC$ в точке $M$. Найдите $BM$, если известно, что $BC=20$, $ACperp BD$ и $BD:AC=3:2$.
Задача по математике — 6851
Окружность, вписанная в равнобедренную трапецию $ABCD$, касается боковых сторон $AB$ и $CD$ в точках $M$ и $N$ соответственно. Отрезок $AN$ пересекает окружность в точке $K$, а луч $MK$ пересекает основание $AD$ в точке $L$.
а) Докажите, что треугольник $AKL$ подобен треугольнику $MAL$.
б) Найдите отношение $AL:LD$.
Задача по математике — 6852
$AA_$, $BB_$ и $CC_$ — высоты остроугольного треугольника $ABC$ с углом $45^$ при вершине $C$.
а) Докажите, что треугольник $A_B_C_$ прямоугольный.
б) Найдите отношение, в котором высота $AA_$ делит отрезок $B_C_$, если известно, $BC=2B_C_$.
🔥 Видео
№368. Найдите углы выпуклого четырехугольника, если они равны друг другу.Скачать

№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

8 класс, 3 урок, ЧетырехугольникСкачать

23. Выпуклые четырехугольникиСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

ОГЭ Задание 24 Площадь выпуклого четырехугольникаСкачать

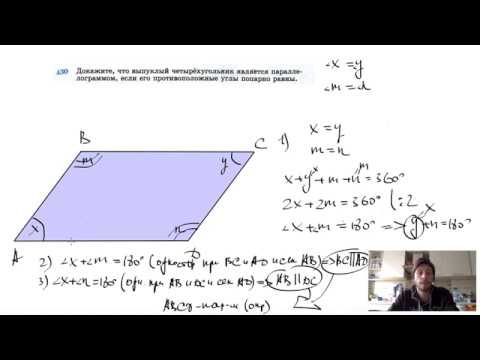
№430. Докажите, что выпуклый четырехугольник является параллелограммом, если его противоположныеСкачать
Многоугольники. Математика 8 класс | TutorOnlineСкачать

13.40.1. Планиметрия. Гордин Р.К.Скачать

🔴 В выпуклом четырёхугольнике ABCD известно ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Задание 24 ОГЭ по математике. Геометрические фигуры. Сумма трех углов выпуклого четырехугольника 300Скачать









