Задание 16. Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра АН к диагонали BD пересекает сторону CD в точке а окружность — в точке F, причём Н — середина АЕ.
а) Докажите, что четырёхугольник BCFE — параллелограмм.
б) Найдите площадь четырёхугольника ABCD, если известно, что АВ = 5 и АН = 4.
а) Точка В лежит на окружности с диаметром CD, поэтому 


б) Треугольник ADE равнобедренный, т.к. его высота DH является медианой, значит, 

Следовательно, треугольник CEF равнобедренный, EF = CF = АВ = 5.
Из прямоугольного треугольника АВН находим, что ВН = 3, значит, высота параллелограмма BCFE (даже ромба), опущенная из вершины Е на сторону ВС, равна 3.
По теореме о произведении отрезков пересекающихся хорд 
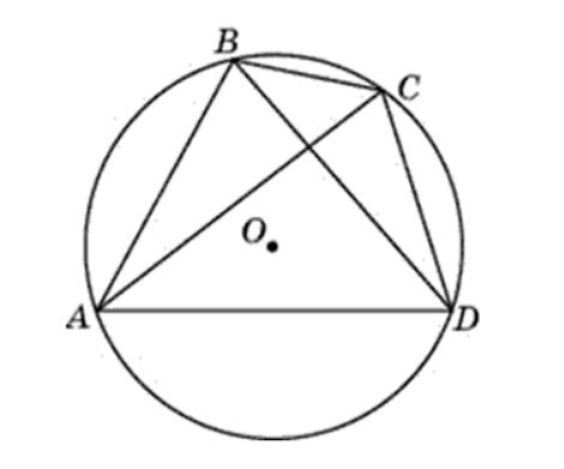
- Задание 16. Математика ЕГЭ. Диагонали AC и BD четырехугольника ABCD, вписанного в окружность, пересекаются в точке Р. Найдите площадь треугольника COD
- Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность
- Общие понятия
- Частные случаи
- Свойства вписанного четырехугольника в окружность
- Теорема 1
- 📸 Видео
Видео:Математика ОГЭ Геометрия Задача 25 Вписанный четырёхугольникСкачать

Задание 16. Математика ЕГЭ. Диагонали AC и BD четырехугольника ABCD, вписанного в окружность, пересекаются в точке Р. Найдите площадь треугольника COD
Задание. Диагонали AC и BD четырехугольника ABCD, вписанного в окружность, пересекаются в точке Р, причем BC = CD.
а) Докажите, что AB : BC = AP : PD.
б) Найдите площадь треугольника COD, где О – центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD – диаметр описанной около четырехугольника ABCD окружности, АВ = 5, а ВС = 5√2.
Рассмотрим треугольники ∆ABC и ∆APD. Вписанные углы ∠BAC = ∠CAD, так как опираются на равные хорды (BC = CD). Вписанные углы ∠ACB = ∠ADB, так как опираются на одну и ту же дугу АВ. Следовательно, треугольники ∆ABC и ∆APD подобные треугольники. Тогда
б) Найдите площадь треугольника COD, где О – центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD – диаметр описанной около четырехугольника ABCD окружности, АВ = 5, а ВС = 5√2.
Так как BD – диаметр окружности, то вписанный угол ∠BCD = 90°, следовательно, треугольник ∆BCD – прямоугольный равнобедренный треугольник. По теореме Пифагора найдем BD:
BD 2 = BC 2 + CD 2
BD 2 = (5√2) 2 + (5√2) 2 = 100
Так как BD – диаметр окружности, то вписанный угол ∠BAD = 90°, следовательно, треугольник ∆BAD – прямоугольный треугольник. В прямоугольном треугольнике ∆BAD гипотенуза BD = 10, катет АВ = 5.
По свойству прямоугольных треугольников: если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Следовательно, угол ∠ADB = 30°, а угол ∠ABD = 60°.
Вписанные углы ∠ABD = ∠ACD, так как опираются на одну и ту же дугу АD, значит, ∠ABD = ∠ACD = ∠ОCD = 60°.
Точка О – центр вписанной в треугольник ∆ABD окружности. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис. Тогда точка О лежит на биссектрисе АС угла ∠BAD и на биссектрисе OD угла ∠ADВ.
Так как угол ∠ADB = 30°, то угол ∠ADO = ∠ODB = 15°. Так как угол ∠BAD = 90°, то угол ∠BAO = ∠OAD = 45°.
Угол ∠СОD – внешний угол треугольника ∆AOD, следовательно, ∠СOD = ∠OAD + ∠ADO = 45° + 15° = 60°. Угол ∠СOD = 60°. Тогда треугольник ∆COD – равносторонний треугольник, в котором OC = OD = CD = 5√2.
Найдем площадь треугольника ∆COD:
Ответ:
Видео:3 правила для вписанного четырехугольника #shortsСкачать

Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность
С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Общие понятия
Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки.
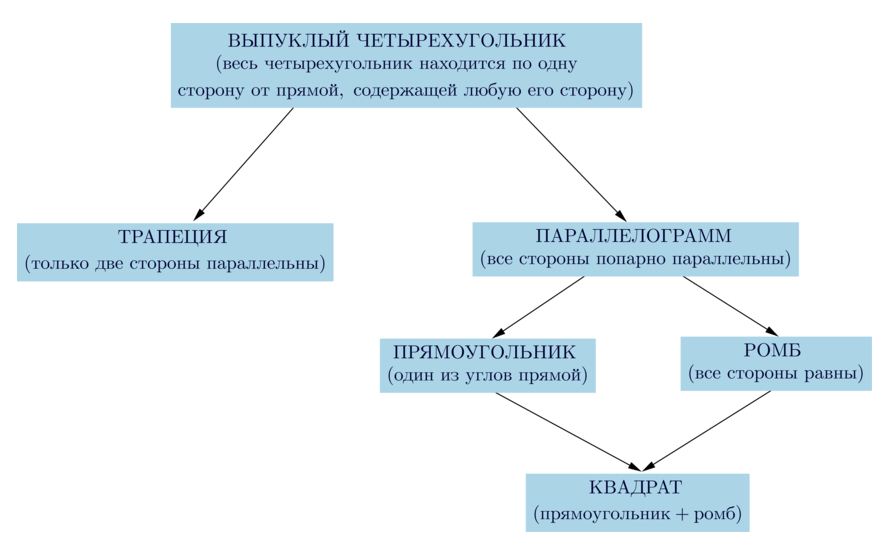
Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры.
Четырехугольник может быть следующих видов:
- Параллелограмм. Параллельность его противоположных сторон доказывается соответствующими теоремами.
- Трапеция. Четырехугольник, у которого основания параллельны. Другие две стороны – нет.
- Прямоугольник. Фигура, у которой все 4 угла = 90º.
- Ромб. Фигура, у которой все стороны равны.
- Квадрат. Совмещает в себя свойства последних двух фигур. У него все стороны равны и все углы прямые.
Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º.
Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Частные случаи
Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи:
- Параллелограмм, как таковой, не может быть вписан в окружность. Только его частный случай. Это прямоугольник.
- Если все вершины ромба находятся на описывающей линии, то он является квадратом.
- Все вершины трапеции находятся на границе окружности. В таком случае говорят о равнобедренной фигуре.
Видео:11 класс, 43 урок, Вписанный четырехугольникСкачать

Свойства вписанного четырехугольника в окружность
Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример.
Видео:#58. Олимпиадная задача о четырехугольникеСкачать

Теорема 1
Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º.
Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что 18 ноября, 2018
📸 Видео
Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Вписанный в окружность четырёхугольник.Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Задача 6 №27875 ЕГЭ по математике. Урок 116Скачать

Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

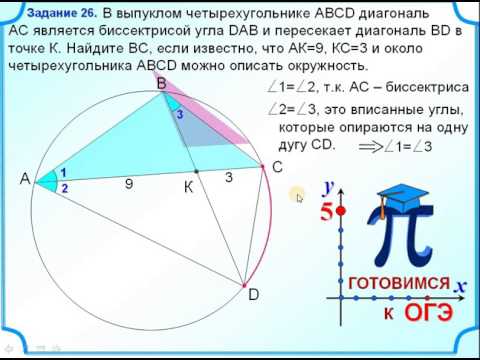
Задание 26 Вписанный четырёхугольникСкачать
Задача №255 [НЕДЕТСКАЯ ГЕОМЕТРИЯ #1]Скачать
![Задача №255 [НЕДЕТСКАЯ ГЕОМЕТРИЯ #1]](https://i.ytimg.com/vi/YOhJB2oYSF4/0.jpg)
№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Задание 25 Вписанный четырёхугольникСкачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать