Дан пространственный четырехугольник abcd m и n середины сторон ab bc cd

Алгебра | 10 — 11 классы

ВЫПОЛНИТЕ ЧЕРТЁЖ К ЗАДАЧЕ Дан пространственный четырёхугольник ABCD, M и N — середины сторон AB и BC соответственно, E принадлежит CD, K принадлежит DA, DE : EC = 1 : 2, DK : KA = 1 : 2.

1)Выполните рисунок к задаче.

Рисунок задачи во вложении ниже.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В выпуклом четырехугольнике abcd отмечены точки k l m и n середины сторон ad, ab, bc, cd соответственно?

В выпуклом четырехугольнике abcd отмечены точки k l m и n середины сторон ad, ab, bc, cd соответственно.

Найдите отношение площади четырехугольника abcd к площади четырёхугольника klmn.

Видео:Решение задач пространственный четырехугольникСкачать

В равнобедренной трапеции ABCD точки F и G являются серединами боковых сторон AB и CD соответственно, отрезок BN — высота трапеции?

В равнобедренной трапеции ABCD точки F и G являются серединами боковых сторон AB и CD соответственно, отрезок BN — высота трапеции.

Найдите периметр четырёхугольника NFGD если средняя линия трапеции равна 10 см, а её боковая сторона — 8 см.

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

В параллелограмме ABCD точка M – середина стороны CD, точка К – середина стороны ВС?

В параллелограмме ABCD точка M – середина стороны CD, точка К – середина стороны ВС.

Выразите через векторы А͞В = а͞ и А͞D = b͞ векторы М͞В и К͞М.

Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Решите задачу, используя круги (диаграммы) Эйлера : множество A состоит из 118 элементов, множество B — из 265 элементов, а множество A пересечённая с B — из 87 элементов Сколько элементов : а) принад?

Решите задачу, используя круги (диаграммы) Эйлера : множество A состоит из 118 элементов, множество B — из 265 элементов, а множество A пересечённая с B — из 87 элементов Сколько элементов : а) принадлежит множеству A, но не принадлежит множеству B б) принадлежит множеству B, но не принадлежит множеству A в) принадлежит множеству A пересечённая с B?

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Не выполняя построение установите принадлежит лиграфику функция Y = sin x + 2?

Не выполняя построение установите принадлежит лиграфику функция Y = sin x + 2.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Точка А принадлежит плоскости α, точка В не принадлежит плоскости α?

Точка А принадлежит плоскости α, точка В не принадлежит плоскости α.

Принадлежит ли плоскости середина отрезка АВ.

Видео:Как строить сечения тетраэдра и пирамидыСкачать

Найдите площадь трапеции ABCD с основаниями AB и CD, если AB = 10см?

Найдите площадь трапеции ABCD с основаниями AB и CD, если AB = 10см.

Видео:Задание №47 — ГДЗ по геометрии 10 класс (Атанасян Л.С.)Скачать

Верно ли , что : а) — 4 принадлежит N ; — 4 принадлежит Z» — 4 принадлежит Q ; б) 5, 6 не принадлежит N ; 5, 6 не принадлежит Z ; 5, 6 не принадлежит Q в) 28 принадлежит N ; 28 принадлежит Z ; 28 прин?

Верно ли , что : а) — 4 принадлежит N ; — 4 принадлежит Z» — 4 принадлежит Q ; б) 5, 6 не принадлежит N ; 5, 6 не принадлежит Z ; 5, 6 не принадлежит Q в) 28 принадлежит N ; 28 принадлежит Z ; 28 принадлежит Q?

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Не выполняя построений выясните принадлежит ли точка А(2 ; — 17) графику функций у = — 4х — 9?

Не выполняя построений выясните принадлежит ли точка А(2 ; — 17) графику функций у = — 4х — 9.

Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Не выполняя построения, ответьте на вопрос : графику какой функции у = х2 или у = — х2 принадлежит заданная точка : а) А ( — 2 ; — 4), В( — 3 ; 9)?

Не выполняя построения, ответьте на вопрос : графику какой функции у = х2 или у = — х2 принадлежит заданная точка : а) А ( — 2 ; — 4), В( — 3 ; 9).

Вы перешли к вопросу ВЫПОЛНИТЕ ЧЕРТЁЖ К ЗАДАЧЕ Дан пространственный четырёхугольник ABCD, M и N — середины сторон AB и BC соответственно, E принадлежит CD, K принадлежит DA, DE : EC = 1 : 2, DK : KA = 1 : 2?. Он относится к категории Алгебра, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Алгебра. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

1) ( (х — 1)·(2х — 1) + (х + 1)·(2х + 1)) / ((2х + 1)·(2х — 1)) = (8х — 1) / (4х² — 1), ( 2х² — х — 2х + 1 + 2х² + х + 2х + 1) / (4х² — 1) = (8х — 1) / (4х² — 1), 4х² — 1≠0 4х² + 2 = 8х — 1, 4х² + 2 — 8х + 1 = 0, 4х² — 8х + 3 = 0, D = 64 — 48 = 16, х..

1) Неопределённость 0 / 0 раскрываем умножением числителя и знаменателя на выражение, сопряжённое знаменателю, т. Е. на В знаменателе разложение разности квадратом, используем это : Сокращаем : 2) Неопределённость (∞ — ∞) раскрываем, приводя к ..

Модуль принимает положительные значения или равен 0, следовательно 1 — x≥0⇒x≤0 x² + x — 12 = 0 x1 + x2 = — 1 U x1 * x2 = — 12⇒x1 = — 4 U x = 3 x∈( — ∞ ; 0] U на промежутке [ — 2 ; 4] целые решения x = — 2 — 1 + 0 + 3 = 0 Отве..

∫√(xˇ10)dx = ∫(xˇ10)ˇ1 / 2dx = ∫(xˇ5)dx = (xˇ6) / 6 + c.

2a — 7 0 Найдём корни квадратного трёхчлена 3a² — 2a + 7 = 0 D / 4 = 1 — 21 = — 20 Дискриминант отрицательный, значит корней нет. Старший член положительный ( 3 > 0), значит 3a² — 2a + 7 больше нуля при любом ..

1)49 + 7 = 45 11 2) — 80 = ( — 35) : ( — 5) — 80 + 7 — 73 3) — 57 + 49 — 8 — 16 4)( — 12) * () 3 * = 1. 5 5) 6)0, 7 — 5 — 4, 3 7)( — 2, 8) : () 7 8)15 : ( — 25) — 0, 6 9) 10)9x = — 720 x = — 80 11)х = 12) — х = .

Видео:Как строить сечения параллелепипедаСкачать

Контрольная работа

Контрольная работа №1.

№1. Основание АD трапеции ABCD лежит в плоскости . Через точки В и С проведены параллельные прямые, пересекающие плоскость в точках E и F соответственно.

а) Каково взаимное положение прямых EF и AB?

б) Чему равен угол между прямыми EF и AB, если ? Поясните ответ.

№2. Дан пространственный четырехугольник ABCD, в котором диагонали AC и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.

а) Выполните рисунок к задаче.

б) Докажите, что полученный четырехугольник есть ромб.

№1. Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону AC. Точка P – середина стороны AD, а K – середина стороны DC.

а) Каково взаимное положение прямых PK и AB?

б) Чему равен угол между прямыми PK и AB, если и ? Поясните ответ.

№2. Дан пространственный четырехугольник ABCD, в котором M и N – середины сторон AB и BC соответственно.

.

а) Выполните рисунок к задаче.

б) Докажите, что четырехугольник MNEK есть трапеция.

Контрольная работа №2.

№1. Прямые а и b лежат в параллельных плоскостях и . Могут ли эти прямые быть:

а) параллельными; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

№2. Через точку О, лежащую между параллельными плоскостями и , проведены прямые l и m. Прямая l пересекает плоскости и в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если , .

№3. Изобразите параллелепипед и постройте его сечение плоскостью, проходящей через точки М, N и К, являющиеся серединами ребер АВ, ВС и DD1.

№1. Прямые а и b лежат в пересекающих плоскостях и . Могут ли эти прямые быть:

а) параллельными; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

№2. Через точку О, не лежащую между параллельными плоскостями и , проведены прямые l и m. Прямая l пересекает плоскости и в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если , .

№3. Изобразите тетраэдр и постройте его сечение плоскостью, проходящей через точки М и N, являющиеся серединами ребер DC и ВС и точку K, такую, что .

Контрольная работа №3.

№1. Диагональ куба равна 6 см. Найдите:

б) косинус угла между диагоналями куба и плоскостью одной из его граней.

№2. Сторона AB ромба ABCD равна a, один из углов равен 60°. Через сторону AB проведена плоскость на расстоянии 0,5a, от точки D.

а) Найдите расстояние от точки С до плоскости .

б) Покажите на рисунке линейный угол двугранного угла DABM, .

в) найдите синус угла между плоскостью ромба и плоскостью .

№1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна см, а его измерения относятся как 1:12 Найдите:

а) измерения параллелепипеда;

б) синус угла между диагональю параллелепипеда и плоскостью его основания.

№2. Сторона квадрата ABCD равна a. Через сторону AD проведена плоскость на расстоянии 0,5a, от точки B.

а) Найдите расстояние от точки С до плоскости .

б) Покажите на рисунке линейный угол двугранного угла BADM, .

в) найдите синус угла между плоскостью квадрата и плоскостью .

Контрольная работа №4.

№1. Основанием пирамиды DABC является правильный треугольник ABC, сторона которого равна a. Ребро DA перпендикулярно к плоскости основания, а плоскость DBC составляет с плоскостью ABC угол в 30°. Найдите площадь боковой поверхности пирамиды.

№1. Основание прямого параллелепипеда является ромб ABCD, сторона которого равна a и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда;

г) площадь полной поверхности параллелепипеда.

№1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, . Найдите площадь поверхности пирамиды.

№1. Основание прямого параллелепипеда является параллелограмм ABCD, сторона которого равна и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:

а) меньшую высоту параллелограмма;

б) угол между плоскостью и плоскостью основания;

в) площадь боковой поверхности параллелепипеда;

г) площадь полной поверхности параллелепипеда.

К-1. Аксиомы стереометрии. Расположение прямых и плоскостей.

№1. Прямые a и b пересекаются. Прямая c является скрещивающейся с прямой a. Могут ли прямые b и c быть параллельными?

№2. Плоскость проходит через середины боковых сторон AB и CD трапеции ABCD – точки M и N.

а) Докажите, что .

б) Найдите BC, если , .

№3. Прямая MА проходит через вершину квадрата ABCD и не лежит в плоскости квадрата.

а) Докажите, что MА и BC – скрещивающиеся прямые.

б) Найдите угол между прямыми MА и BC, если .

№1. Прямые a и b пересекаются. Прямые a и c параллельны. Могут ли прямые b и c быть скрещивающимися?

№2. Плоскость проходит через основание AD трапеции ABCD. M и N – середины боковых сторон трапеции.

а) Докажите, что .

б) Найдите AD, если, .

№3. Прямая CD проходит через вершину треугольника ABC и не лежит в плоскости ABC. E и F – середины отрезков AB и BC.

а) Докажите, что CD и EF – скрещивающиеся прямые.

б) Найдите угол между прямыми CD и EF, если .

№1. Прямая a параллельна плоскости , а прямая b лежит в плоскости . Определите, могут ли прямые a и b:

а) быть параллельными;

в) быть скрещивающимися.

№2. Точка M не лежит в плоскости трапеции ABCD, .

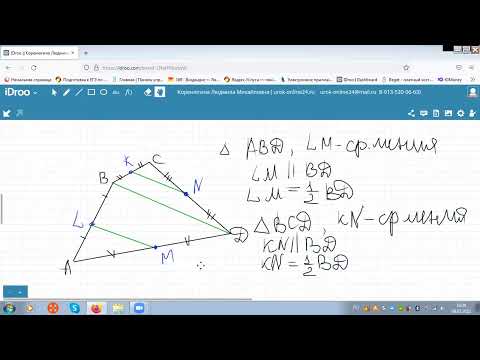
а) Докажите, что треугольники MAD и MBC имеют параллельные средние линии.

б) Найдите длины этих средних линий, если , а средняя линия трапеции равна 16 см.

№3. Через вершину А квадрата ABCD проведена прямая KA, не лежащая в плоскости квадрата.

а) Докажите, что KА и CD – скрещивающиеся прямые.

б) Найдите угол между KА и CD, если , .

№1. Прямая a параллельна плоскости , а прямая b пересекает плоскость . Определите, могут ли прямые a и b:

а) быть параллельными;

в) быть скрещивающимися.

№2. Треугольник ABC и трапеция KMNP имеют общую среднюю линию EF, причем ,

а) Докажите, что

б) Найдите KP и MN, если , .

№3. Точка M не лежит в плоскости ромба ABCD.

а) Докажите, что MC и AD – скрещивающиеся прямые.

б) Найдите угол между MC и AD, если , .

№1. Плоскости и пересекаются по прямой l. Прямая a параллельна прямой l, и является скрещивающейся с прямой b. Определите, могут ли прямые a и b:

а) лежать в одной из данных плоскостей;

б) лежать в разных плоскостях и ;

в) пересекать плоскости и .

В случае утвердительного ответа укажите взаимное расположение прямых a и b.

№2. Плоскость пересекает стороны AB и BC треугольника ABC в точках M и N соответственно, причем ,

а) Докажите, что .

б) Найдите AC, если .

№3. Точки А, B, C, D не лежат в одной плоскости. Найдите угол между прямыми АC и BD, если , , а расстояние между серединами отрезков AD и BC равно 5 см.

№1. Плоскости и пересекаются по прямой l. Прямые l и a пересекаются, а прямые l и b параллельны. Определите, могут ли прямые a и b:

а) лежать в одной из данных плоскостей;

б) лежать в разных плоскостях и ;

в) пересекать плоскости и .

В случае утвердительного ответа укажите взаимное расположение прямых a и b.

№2. Плоскость проходит через сторону AC треугольника ABC. Прямая пересекает стороны AB и BC в точках M и N соответственно, причем ,

а) Докажите, что .

б) Найдите MN, если .

№3. Точки А, B, C, D не лежат в одной плоскости. Найдите угол между прямыми АB и CD, если , а расстояние между серединами отрезков AD и BC равно 3 см.

К-2. Перпендикулярность прямых и плоскостей.

№1. КА – перпендикуляр к плоскости треугольника АВС. Известно что КВ ^ ВС.

а) Докажите, что треугольник АВС – прямоугольный.

б) Докажите перпендикулярность плоскостей КАС и АВС.

в) Найдите КА, если , , .

№2. Основание АС равнобедренного треугольника лежит в плоскости . Найдите расстояние от точки В до плоскости , если , , а двугранный угол между плоскостями АВС и равен 30°.

№3. Из точки А к плоскости проведены наклонные АВ и АС, образующие с плоскостью равные углы. Известно, что . Найдите углы треугольника АВС.

№1. КА – перпендикуляр к плоскости параллелограмма ABCD. Известно, что KD ^ CD.

а) Докажите, что ABCD – прямоугольник.

б) Докажите перпендикулярность плоскостей KAD и ABC.

в) Найдите АС, если , , .

№2. Катет АВ прямоугольного треугольника АВС () лежит в плоскости . Найдите расстояние от точки С до плоскости , если , , а двугранный угол между плоскостями АВС и равен 45°.

№3. Из точки А к плоскости проведены перпендикуляр АО и две равные наклонные АВ и АС. Известно, что . Найдите углы треугольника ВОС.

№1. КА – перпендикуляр к плоскости треугольника АВС. М – середина стороны ВС. Известно, что КМ ^ ВС.

а) Докажите, что треугольник АВС – равнобедренный.

б) Докажите перпендикулярность плоскостей КВС и КАМ.

в) Найдите площадь треугольника АВС, если , , см.

№2. Точка S удалена от каждой из вершин правильного треугольника АВС на см. Найдите двугранный угол SABC, если .

№3. Прямая АВ – ребро двугранного угла, равного 90°. Прямые АА1 и ВВ1 принадлежат разным граням данного угла и перпендикулярны к прямой АВ. Докажите, что АА1^ВВ1.

№1. КА – перпендикуляр к плоскости параллелограмма ABCD. О – точка пересечения АС и BD. Известно, что КО ^ BD.

а) Докажите, что ABCD – ромб.

б) Докажите перпендикулярность плоскостей KBD и КОА.

в) Найдите площадь ABCD, если , , .

№2. Точка S удалена от каждой из сторон правильного треугольника АВС на см. Найдите угол между прямой SA и плоскостью АВС, если .

№3. Прямые АА1 и ВВ1 – перпендикуляры к ребру АВ двугранного угла, принадлежащие разным граням угла. Докажите, что если АА1^ВВ1, то данный двугранный угол – прямой.

№1. Точка О лежит на биссектрисе угла АВС, равного 60°. DО – перпендикуляр к плоскости АВС.

а) Докажите, что точка D равноудалена от сторон угла АВС.

б) Пусть DA и DC – расстояния от точки D до сторон угла. Докажите перпендикулярность плоскостей DAC и DOB.

в) Найдите DB, если , .

№2. Равнобедренные треугольники АВС и АDC имеют общее основание АС, а двугранный угол ВАСD – прямой. Найдите углы, образуемые прямой BD с плоскостями треугольников, если , а .

№3. В кубе АВСDA1B1C1D1 постройте и найдите линейный угол двугранного угла между плоскостями сечений АВ1С1D и СВ1А1D.

№1. DO – перпендикуляр к плоскости угла АВС, равного120°, причем точка О лежит внутри угла, а D равноудалена от его сторон.

а) Докажите, что ВО – биссектриса угла АВС.

б) Пусть DA и DC – расстояния от точки D до сторон угла. Докажите перпендикулярность плоскостей DOB и DAC.

в) найдите DO, если , .

№2. Равнобедренные треугольники АВС и ADC имеют общее основание АС, а двугранный угол BACD – прямой. Найдите тангенс двугранного угла между плоскостями BAD и АDС, если , а .

№3. В кубе АВСDA1B1C1D1 постройте и найдите линейный угол двугранного угла между плоскостями сечений CD1A1B и DA1B1C.

№1. Основание прямой призмы – прямоугольный треугольник с катетами 6 и 8 см. Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань – квадрат.

№2. Боковое ребро правильной четырехугольной пирамиды равно

4 см и образует с плоскостью основания пирамиды угол 45°.

а) Найдите высоту пирамиды.

б) Найдите площадь боковой поверхности пирамиды.

№3. Ребро правильного тетраэдра DABC равно a. Постройте сечение тетраэдра, проходящее через середину ребра DA параллельно плоскости DBC, и найдите площадь этого сечения.

№1. Основание прямой призмы – прямоугольный треугольник с гипотенузой 13 см и катетом 12 см. Найдите площадь боковой поверхности призмы, если ее наименьшая боковая грань – квадрат.

№2. Высота правильной четырехугольной пирамиды равна см, боковое ребро наклонено к плоскости основания под углом 60°.

а) Найдите боковое ребро пирамиды.

б) Найдите площадь боковой поверхности пирамиды.

№3. Ребро правильного тетраэдра DABC равно a. Постройте сечение тетраэдра, проходящее через середины ребер DA и AB параллельно ребру BC, и найдите площадь этого сечения.

№1. Основание прямого параллелепипеда – ромб с диагоналями 10 и 24 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол 45°. Найдите площадь полной поверхности параллелепипеда.

№2. Основание пирамиды – правильный треугольник с площадью см2. Две боковые грани пирамиды перпендикулярны к плоскости основания, а третья – наклонена к ней под углом 30°.

а) Найдите длины боковых ребер пирамиды.

б) Найдите площадь боковой поверхности пирамиды.

№3. Ребро куба АВСDA1B1C1D1 равно a. Постройте сечение куба, проходящее через прямую B1C и середину ребра AD, и найдите площадь этого сечения.

№1. Основание прямого параллелепипеда – ромб с меньшей диагональю 12 см. Большая диагональ параллелепипеда равна см и образует с боковым ребром угол 45°. Найдите площадь полной поверхности параллелепипеда.

№2. Основание пирамиды – равнобедренный прямоугольный треугольник с гипотенузой см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 45°.

а) Найдите длины боковых ребер пирамиды.

б) Найдите площадь боковой поверхности пирамиды.

№3. Ребро куба АВСDA1B1C1D1 равно a. Постройте сечение куба, проходящее через точку C и середину ребра AD параллельно прямой DA1, и найдите площадь этого сечения.

№1. Основание прямой призмы – прямоугольный треугольник с катетами 15 и 20 см. Найдите площадь полной поверхности призмы, если ее наименьшее сечение, проходящее через боковое ребро, – квадрат.

№2. Основание пирамиды – ромб с большей диагональю d и острым углом . Все двугранные углы при основании пирамиды равны . Найдите площадь полной поверхности пирамиды.

№3. Ребро куба АВСDA1B1C1D1 равно a. Постройте сечение куба, проходящее через середины ребер AA1, B1C1 и CD, и найдите площадь этого сечения.

№1. Основание прямой призмы – равнобедренный треугольник с основанием 24 м и боковой стороной 13 см. Найдите площадь полной поверхности призмы, если ее наименьшее сечение, проходящее через боковое ребро, – квадрат.

№2. Основание пирамиды – ромб с тупым углом . Все двугранные углы при основании пирамиды равны . Найдите площадь полной поверхности пирамиды, если ее высота равна H.

№3. Ребро куба АВСDA1B1C1D1 равно a. Постройте сечение куба, проходящее через середины ребер A1B1, CC1 и AD, и найдите площадь этого сечения.

К-4. Векторы в пространстве.

№1. Дан куб АВСDA1B1C1D1.

а) Назовите вектор с началом в точке D1, равный вектору .

б) Назовите вектор, равный .

б) Назовите вектор , удовлетворяющий равенству .

№2. В правильном тетраэдре DABC с ребром a точка О – центр треугольника ABC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. MA – перпендикуляр к плоскости ромба ABCD. Разложите вектор по векторам .

№4. Векторы неколлинеарные. Найдите значение k, при которых векторы и коллинеарные.

№1. Дан куб АВСDA1B1C1D1.

а) Назовите вектор с концом в точке C1, равный вектору .

б) Назовите вектор, равный .

б) Назовите вектор , удовлетворяющий равенству .

№2. В правильном тетраэдре DABC с ребром a точка О – центр треугольника ABC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. MB – перпендикуляр к плоскости треугольника ABC. Разложите вектор по векторам .

№4. Векторы неколлинеарные. Найдите значение k, при которых векторы и коллинеарные.

№1. Дан параллелепипед АВСDA1B1C1D1.

а) Назовите вектор с началом в точке D, равный вектору .

б) Назовите вектор, равный ; в) .

г) Назовите вектор , удовлетворяющий равенству .

№2. В правильном тетраэдре DABC с ребром a точка О – центр треугольника ABC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. Точка О не лежит в плоскости параллелограмма ABCD. Разложите вектор по векторам .

№4. Даны параллелограммы ABCD и ABC1D1. Докажите, что векторы компланарны.

№1. Дан параллелепипед АВСDA1B1C1D1.

а) Назовите вектор с концом в точке B1, равный вектору .

б) Назовите вектор, равный ; в) .

г) Назовите вектор , удовлетворяющий равенству .

№2. В правильном тетраэдре DABC с ребром a точка О – центр треугольника ABC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. Точка О не лежит в плоскости параллелограмма ABCD. Разложите вектор по векторам .

№4. Даны параллелограммы ABCD и A1B1CD. Докажите, что векторы компланарны.

№1. Дан правильный октаэдр EАВСDF.

а) Назовите вектор с началом в точке B,

равный .

б) Назовите вектор, равный ;

в) вектор равный .

г) Назовите вектор , удовлетворяющий

равенству .

№2. В правильном тетраэдре DABC с ребром a, точка P – центр треугольника ABC, точка Q – центр треугольника BDC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. Точка S равноудалена от вершин треугольника ABC (). SO – перпендикуляр к плоскости ABC. Разложите вектор по векторам .

№4. Точки M и N – середины ребер BD и AC правильного тетраэдра DABC. Докажите, что векторы компланарны.

№1. Дан правильный октаэдр EАВСDF.

а) Назовите вектор с концом в точке C,

равный .

б) Назовите вектор, равный ;

в) вектор равный .

г) Назовите вектор , удовлетворяющий

равенству .

№2. В правильном тетраэдре DABC с ребром a, точка P – центр треугольника ABC, точка Q – центр треугольника BDC.

а) Постройте вектор и найдите его длину.

б) Найдите .

№3. Точка S равноудалена от сторон ромба ABCD. SO – перпендикуляр к плоскости ромба. Разложите вектор по векторам .

№4. Точки M и N – середины ребер AD и BC правильного тетраэдра DABC. Докажите, что векторы компланарны.

Контрольная работа № 5.

№1. Дан прямоугольный треугольник с гипотенузой и катетом . Отрезок , равный 12 см, – перпендикуляр к плоскости .

а) Найдите .

б) Найдите угол между прямой и плоскостью .

№2. В правильной четырехугольной пирамиде диагональ основания равна см, а двугранный угол при основании равен 60°. Найдите площадь полной поверхности пирамиды.

№3. Постройте сечение куба , проходящее через вершину и середины ребер и . Определите вид многогранника, полученного в сечении.

№1. Дан прямоугольный треугольник с катетами и . Отрезок , равный 20 см, – перпендикуляр к плоскости .

а) Найдите .

б) Найдите угол между прямой и плоскостью .

№2. В правильной четырехугольной пирамиде высота равна см, а двугранный угол при основании равен 60°. Найдите площадь полной поверхности пирамиды.

№3. Постройте сечение куба , проходящее через прямую и середину ребра . Определите вид многогранника, полученного в сечении.

№1. Диагонали ромба пересекаются в точке . – перпендикуляр к плоскости ромба. см, см, см.

а) Докажите, что прямая перпендикулярна к плоскости .

б) Найдите .

в) Найдите двугранный угол .

№2. В правильной треугольной пирамиде плоский угол при вершине равен 120°. Отрезок, соединяющий основание высоты пирамиды с серединой бокового ребра, равен 3 см. Найдите площадь полной поверхности пирамиды.

№3. Постройте сечение правильного тетраэдра , проходящее через середины ребер и параллельно ребру . Определите вид многогранника, полученного в сечении.

№1. Диагонали ромба пересекаются в точке . – перпендикуляр к плоскости ромба. см, см, см.

а) Докажите перпендикулярность плоскостей и .

б) Найдите .

в) Найдите угол между прямой и плоскостью.

№2. В правильной треугольной пирамиде двугранный угол при основании равен 60°. Отрезок, соединяющий основание высоты пирамиды с серединой апофемы, равен 3 см. Найдите площадь полной поверхности пирамиды.

№3. Постройте сечение правильного тетраэдра , проходящее через середины ребер и параллельно ребру . Определите вид многогранника, полученного в сечении.

№1. Дан равнобедренный прямоугольный треугольник с гипотенузой . – перпендикуляр к плоскости . Двугран-ный угол равен 45°.

а) Докажите перпендикулярность плоскостей и .

б) – точка пересечения медиан треугольника .

Разложите вектор по векторам .

в) Найдите углы наклона прямых и к плоскости .

№2. Основание пирамиды – прямоугольный треугольник с катетом a и противолежащим углом . Боковые грани пирамиды, содержащие данный катет и гипотенузу основания, перпендикулярны к плоскости основания, а третья боковая грань наклонена к ней под углом . Найдите площадь боковой поверхности пирамиды.

№3. Постройте сечение правильной четырехугольной пирамиды , проходящее через середины ребер основания и параллельно боковому ребру .

№1. Дан равнобедренный прямоугольный треугольник с гипотенузой . – перпендикуляр к плоскости . Прямые и образуют с плоскостью угол 30°.

а) Докажите перпендикулярность плоскостей и , если – середина .

б) – точка пересечения медиан треугольника .

Разложите вектор по векторам .

в) Найдите двугранный угол .

№2. Основание пирамиды – прямоугольный треугольник с гипотенузой с и острым углом . Боковые грани пирамиды, содержащие катеты основания, перпендикулярны к плоскости основания, а третья боковая грань наклонена к ней под углом . Найдите площадь боковой поверхности пирамиды.

№3. Постройте сечение правильной четырехугольной пирамиды , проходящее через середины ребра основания и бокового ребра параллельно прямой .

Видео:№ 107 - Геометрия 8 класс МерзлякСкачать

Презентация по математике на тему «Решение задач. Пространственный четырехугольник»

Видео:ЕГЭ Математика 16 Задание Планиметрическая задача Четырехугольники Середины сторонСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Пространственый четырехугольник. Решение задач. гимназия 64 учитель математики Котельникова Н. В.

Доказательство Пусть нам дан пространственный четырехугольник ABCD. M, N, K, L – середины ребер BD, AD, AC, BC соответственно. Нужно доказать, что MNKL – параллелограмм. Рассмотрим треугольник АВD. МN – средняя линия. По свойству средней линии, МN параллельна АВ и равняется ее половине. Рассмотрим треугольник АВС. LК – средняя линия. По свойству средней линии, LК параллельна АВ и равняется ее половине. И МN, и LК параллельны АВ. Значит, МN параллельна LК по теореме о трех параллельных прямых. Получаем, что в четырехугольнике MNKL – стороны МN и LК параллельны и равны, так как МN и LК равны половине АВ. Значит, по признаку параллелограмма, четырехугольник MNKL – параллелограмм, что и требовалось доказать.

Четырехугольник называется пространственным, если его вершины не лежат в одной плоскости. № 1.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 955 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 702 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 337 человек из 71 региона

Ищем педагогов в команду «Инфоурок»

• Котельникова Наталья ВячеславовнаНаписать 4688 07.01.2019

Номер материала: ДБ-345782

07.01.2019 235

07.01.2019 135

07.01.2019 169

07.01.2019 216

07.01.2019 245

05.01.2019 83

30.12.2018 404

29.12.2018 174

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения готовит рекомендации по построению «идеальной школы»

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Детский омбудсмен предложила ужесточить наказание за преступления против детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

№ 47 - Геометрия 10-11 класс АтанасянСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

№ 43 - Геометрия 10-11 класс АтанасянСкачать

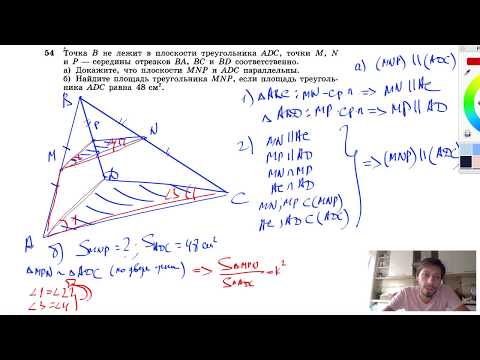
№54. Точка В не лежит в плоскости треугольника ADC, точки М, N и Р — середины отрезков ВА, ВССкачать

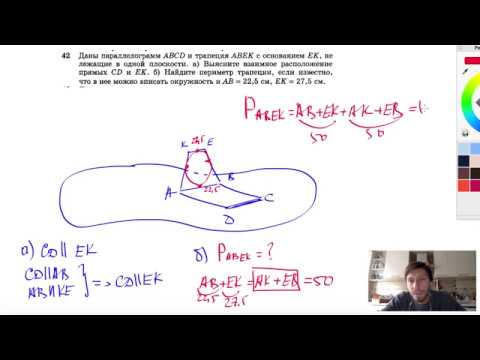
№42. Даны параллелограмм ABCD и трапеция ABEK с основанием ЕК, не лежащие в одной плоскости,Скачать

3 правила для вписанного четырехугольника #shortsСкачать