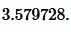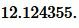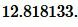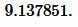Радиус окружности является биссектрисой равнобедренного треугольника

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла

Формулы для радиуса окружности, вписанной в треугольник

Вывод формул для радиуса окружности, вписанной в треугольник

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла

Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.

Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).

Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).

Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.

Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.

Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).

Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно

что и требовалось доказать.

Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.

Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.

Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.

Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).

Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать

Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .

Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.

Формулы для радиуса окружности, вписанной в треугольник

Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.

a, b, c – стороны треугольника,
S – площадь,
r – радиус вписанной окружности,
p – полупериметр

.

a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Фигура	Рисунок	Формула	Обозначения
Произвольный треугольник
		Равнобедренный треугольник
Равносторонний треугольник
Прямоугольный треугольник

где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
.

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
.

где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Произвольный треугольник
	Равнобедренный треугольник
Равносторонний треугольник
Прямоугольный треугольник

Произвольный треугольник

где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр
.

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр
.

Равнобедренный треугольник

Равносторонний треугольник

где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Прямоугольный треугольник

Вывод формул для радиуса окружности, вписанной в треугольник

Теорема 5 . Для произвольного треугольника справедливо равенство

где a, b, c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).

с помощью формулы Герона получаем:

что и требовалось.

Теорема 6 . Для равнобедренного треугольника справедливо равенство

где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).

то, в случае равнобедренного треугольника, когда

что и требовалось.

Теорема 7 . Для равностороннего треугольника справедливо равенство

где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).

то, в случае равностороннего треугольника, когда

что и требовалось.

Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.

Теорема 8 . Для прямоугольного треугольника справедливо равенство

Доказательство . Рассмотрим рисунок 9.

Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,

В силу теоремы 3 справедливы равенства

Следовательно, принимая также во внимание теорему Пифагора, получаем

что и требовалось.

Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.

Как связаны биссектриса и окружность

В геометрии могут объединиться даже очень различные на первый взгляд фигуры, такие как окружность и треугольник. У каждой есть свои особенности, которые позволяют отличать их от прочих фигур, даже если они очень похожи: например, круг и окружность – это совсем не одно и тоже.

Разница между кругом и окружностью состоит в отношении к плоскости. Если упрощенно, то под плоскостью понимают поверхность, на которой и строятся фигуры. Саму плоскость тоже можно считать фигурой. Окружность – это совокупность всех точек на плоскости, которые образуют фигуру, а круг – это часть плоскости, которую ограничивает окружность. Поэтому может быть сектор или сегмент круга – но понятие дуги относится только к окружности.

Одним из важнейших понятий, связанных с окружностью, является радиус – расстояние от центра окружности до любой её точки. Чтобы произвести вычисление радиуса, нужно знать длину окружности, её площадь или диаметр. Проще всего посчитать радиус через диаметр – просто разделить длину диаметра на два.

Зная длину, тоже можно вычислить радиус – если формула длины – это L=2πR, то радиус вычисляется по формуле R= L/2π.

Окружность можно как вписать в любой треугольник, так и начертить вокруг любого треугольника так, чтобы все вершины треугольника касались окружности. Чтобы описать окружность вокруг треугольника, надо найти точку пересечения всех углов треугольника – она будет центром описываемой окружности. Чтобы, напротив, вписать круг в треугольник, надо к середине каждой стороны провести перпендикулярную прямую. Точка их пересечения и будет центром вписанного круга.

Основное свойство вписанного в окружность треугольника состоит в том, что вычислить его площадь очень просто – для этого надо знать радиус окружности и длины сторон треугольника. Для этого используется формула: P/2*R, где P – периметр, а R – радиус окружности.

Значение биссектрисы – луча, исходящего из вершины угла и делящего его напополам, – не ограничивается тем, что с её помощью можно вписать круг в треугольник. Назовем основные свойства биссектрисы треугольника, которые существенно облегчают процесс решения геометрических задач.

Во-первых, биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам. Во-вторых, в правильном треугольнике биссектриса является медианой и высотой, а в равнобедренном треугольнике совпадает с медианой и с высотой только в том случае, если проведена от вершины к основанию. В-третьих, как уже упоминалось, биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник.

При решении задач, связанных с треугольниками или окружностями, важно отличать биссектрису от медианы или высоты, а радиус или диаметр – от хорды.

Радиус описанной окружности около равнобедренного треугольника онлайн

С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Открыть онлайн калькулятор

1. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и боковая сторона b=c

Пусть известны основание a равнобедренного треугольника и боковая сторона b=c. Найдем радиус описанной окружности около равнобедренного треугольника. На странице Радиус окружности описанной около треугольника онлайн была выведена формула вычисления радиуса R описанной около любого треугольника окружности:

( small R=frac<large 4 cdot sqrt >. )

(1)

где p вычисляется из формулы:

( small p= frac. )

(2)

Учитывая, что у нас треугольник равнобедренный, т.е. b=c, имеем:

( small p= frac=b+ frac, )

(3)

( small p-a= b- frac, )

(4)

( small p-b= frac, )

(5)

Подставляя (3)−(5) в (1) и учитывая, что b=c, получим:

( small R=frac<large 4 cdot frac cdot sqrt<left ( b+fracright)left ( b-fracright)>> ) ( small =frac<large 2 cdot sqrt< b^2-frac>> ) ( small =frac< sqrt> ,)

( small R=frac< sqrt>. )

(6)

Пример 1. Известны основание ( small a=7 ) и боковая сторона ( small b=frac ) равнобедренного треугольника. Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (6).

Подставим значения ( small a=7 ) и ( small b=frac ) в (6):

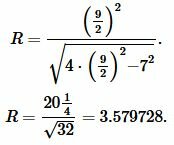Ответ:

2. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и противолежащий угол A

Пусть известны сторона a и противолежащий угол A. Формула для нахождения радиуса окружности описанной около равнобедренного треугольника по основанию и противолежащему углу аналогична формуле для нахождения радиуса окружности описанной около произвольного треугольника:

.

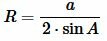(7)

Пример 2. Сторона основание равнобедренного треугольника равна:( small a=21 ) а противолежащий угол ( small angle A=60°.) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения ( small a=21 ) и ( small angle A=60° ) в (7):

.

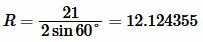Ответ:

3. Радиус окружности описанной около равнобедренного треугольника, если известны боковая сторона b=c треугольника и угол между боковыми сторонами A

Пусть известны боковая сторона b=c равнобедренного треугольника и угол между боковыми сторонами A. Найдем радиус описанной окружности около равнобедренного треугольника.

На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известных сторонах и углу между ними:

.

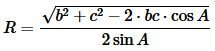(8)

Подставляя в (8) c=b, получим:

.

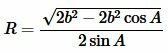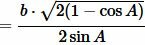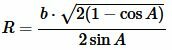(9)

Пример 3. Известны основание ( small a=21 ) равнобедренного треугольника и угол между боковыми сторонами: ( small angle A=70°. ) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (9). Подставим значения ( small a=21; ) и ( small angle A=70° ) в (9):

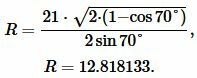Ответ:

4. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и прилежащий угол B=C

Пусть известны основание a равнобедренного треугольника и прилежащие к ней угол B=C. Найдем радиус описанной окружности около треугольника. На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известной стороне и прилежащим двум углам:

.

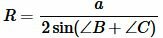(10)

Подставляя ( small C=B ) в (10), получим требуемую формулу:

.

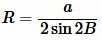(11)

Пример 4. Известны основание равнобедренного треугольника ( small a=14 ) и прилежащий к ней угол: ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (11). Подставим значения ( small a=14 ) и ( small angle B=25° ) в (11):

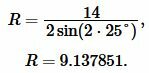Ответ:

🔍 Видео