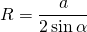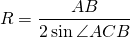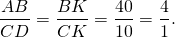Четырехугольник abcd вписан в окружность к точка пересечения диагоналей

Геометрия | 10 — 11 классы

Четырехугольник авсд вписан в окружность, к — точка пересечения диагоналей ас и вд.

Докажите, что ак * ск = вк * дк Пожалуйста можно подробно.

Решение во вложенном файле.

Видео:Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

В четырехугольнике АВСД вписана окружность, АВ = 5, СД = 15?

В четырехугольнике АВСД вписана окружность, АВ = 5, СД = 15.

Найдите периметр четырехугольника.

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Прямоугольник АВСД вписан в окружность с центром в точке О — точке пересечения диагоналей прямоугольника?

Прямоугольник АВСД вписан в окружность с центром в точке О — точке пересечения диагоналей прямоугольника.

Найдите длины сторон прямоугольника АВСД, если известно, что одна из них вдвое больше другой, а диагональ окружности АС = 14√15 см.

ПОМОГИТЕ, ОЧЕНЬ НУЖНО!

Заранее спасибо огромное!

Видео:Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

Найти углы четырехугольника АВСД, вписанного в окружность, если уголВ : углуД = 5 : 4?

Найти углы четырехугольника АВСД, вписанного в окружность, если уголВ : углуД = 5 : 4.

Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

В окружность длиной 8пи см вписан правильный четырехугольник?

В окружность длиной 8пи см вписан правильный четырехугольник.

Тогда диагональ данного четырехугольника будет равна?

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Докажите что вершины прямоугольника лежат на окружности с центром в точке пересечения его диагоналей?

Докажите что вершины прямоугольника лежат на окружности с центром в точке пересечения его диагоналей.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Точка пересечения диагоналей четырехугольника ABCM является центром его симметрии ?

Точка пересечения диагоналей четырехугольника ABCM является центром его симметрии .

Докажите что ABCM — параллелограмм.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Докажите, что если в четырехугольник АВСД вписана окружность с центром в точке О, то угол АОВ + угол СОД = 180 градусов?

Докажите, что если в четырехугольник АВСД вписана окружность с центром в точке О, то угол АОВ + угол СОД = 180 градусов.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Прямоугольник АВСД вписан в окружность с центром в точке О — точке пересечения диагоналей прямоугольника?

Прямоугольник АВСД вписан в окружность с центром в точке О — точке пересечения диагоналей прямоугольника.

Найдите длины сторон прямоугольника АВСД, если известно, что одна из них вдвое больше другой, а диагональ окружности АС = 14√15 см.

ПОМОГИТЕ, ОЧЕНЬ НУЖНО!

Заранее спасибо огромное!

Видео:Четырёхугольник ABCD вписан в окружность. Угол ABD равен 80°, угол CAD равен 34°. Найдите угол АВС.Скачать

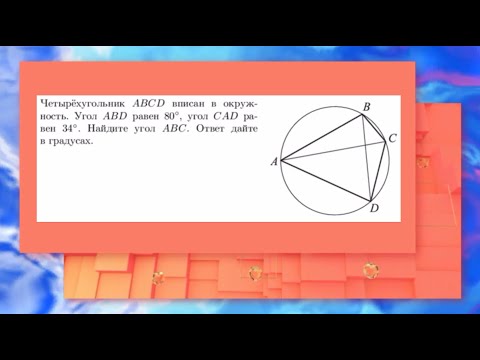
Четырехугольник ABCD вписан в окружность, О — точка пересечения его диагоналей?

Четырехугольник ABCD вписан в окружность, О — точка пересечения его диагоналей.

Угол ABD = 72 градуса.

Угол BDC = 36 градуса.

Найдите угол между прямыми AB и DC.

Видео:Решение задачи 25 из ОГЭ по математике 9 классСкачать

Трапеция АВСД вписана в окружность (О — центр окружности)?

Трапеция АВСД вписана в окружность (О — центр окружности).

АД — большее основание.

Докажите, что углы В и С трапеции АВСД равны.

На этой странице вы найдете ответ на вопрос Четырехугольник авсд вписан в окружность, к — точка пересечения диагоналей ас и вд?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Во вписанном 4х — угольнике сумма противоположных углов равна 180°. 101° + 113° ≠ 180° ⇒ они не противоположные 180° — 101° = 79° третий угол 180° — 113° = 67° четвёртый угол Наибольшим из этих четырёх углов является угол в 113°. Ответ : 113°.

Х + 2(х + 42) = 180x = 32 (первый угол)2(32 + 42) = 148 — второй.

1)Если в треугольнике две стороны равны, то он равнобедренный(поопределению).

Так как треугольники равны, угол М = 30° В = 60° С = 90°.

AB = AC + BC = 15 + 27 = 42 см.

50 : 2 = 25 4 + 1 = 5 25 : 5 = 5 5 * 4 = 20 5 * 1 = 5 Ответ : 5, 25.

Смотрите три чертежа ниже ↓ .

1) Рассмотрим треугольник KMH : ∠ HKM = 23°, ∠MHK = 90° — по условию, тогда ∠KMC = 180 — ∠ HKM — ∠MHK = 180 — 23 — 90 = 67° ∠MKC = ∠ HKM + ∠HKC = 23° + 44° = 67° ∠MCK = 180° — ∠KMC — ∠MKC = 180 — 67 — 67 = 46° Т. К. два угла раны (∠KMC = ∠MKC), знач..

Вот даю альтернативное решение тому, какому дала уважаемая Hrisula / решение смотри в файле.

Срединный перпендикуляр диагонали АС прямоугольника АВСD пересекает сторону ВС и образует с ней угол, равный углу между диагоналями. Найдите этот угол. Срединный перпендикуляр проведен к точке пересечения диагоналей, которая делит их пополам. Обоз..

Видео:Г: Четырехугольник ABCD вписан в окружность так, что сторона AD является диаметром этой окружностиСкачать

Четырёхугольник ABCD вписан в окружность, Р — точка пересечения диагоналей четырёхугольника. Докажите, что АР* РС= ВР*PD.

Видео:Геометрия Четырёхугольник ABCD со сторонами AB = 2 и CD = 5 вписан в окружность. Диагонали AC и BDСкачать

Ваш ответ

Видео:Четырёхугольник ABCD вписан в окружность. Угол ABC=122, угол ABD=36. Найти угол CADСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,049
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Четырёхугольник ABCD вписан в окружность причём BC CD Известно что угол ADC равен 93Скачать

Четырехугольник ABCD вписан в окружность

Четырехугольник ABCD со сторонами AB=40 и CD=10 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60º. Найти радиус окружности, описанной около этого четырёхугольника.

Дано : ABCD — четырёхугольник, вписанный в окружность (O;R), AB=40, CD=10, AC∩BD=K, ∠AKB=60º

Радиус описанной около четырёхугольника окружности можно найти как радиус окружности, описанной около любого из треугольников, образованной вершинами четырёхугольника, например, около треугольника ABC. Если использовать формулу

для стороны AB, то искомый радиус

Длина AB известна. Значит, задача сводится к нахождению синуса угла ACB.

Рассмотрим треугольники ABK и DCK.

2)∠AKB=∠DKC (как вертикальные).

Следовательно, треугольники ABK и DCK подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Пусть CK=x, тогда BK=4x.

Рассмотрим треугольник BCK.

∠BKC+∠AKB=180º (как смежные), отсюда ∠BKC=180º-∠AKB=120º. По теореме косинусов

💡 Видео

Задача 6 №27876 ЕГЭ по математике. Урок 117Скачать

Четырехугольник АВСD со сторонами АВ=12 иСD=13 вписан в окружность. 27 вариант Ященко ОГЭ задача 25Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

2151 четырёхугольник ABCD вписан в окружность Угол ABC равен 48 угол cаd равен 38 Найдите угол абдСкачать

#29. Регион ВсОШ 2023, 9.5Скачать

2128 в четырёхугольник ABCD вписана окружность AB = 7 BC = 12 CD = 9Скачать