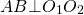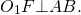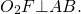Общая хорда двух пересекающихся окружностей перпендикулярна прямой, проходящей через центры этих окружностей.
Дано : окр. (O1; R) ∩ окр. (O2; r)=A, B.
Соединим центры окружностей с точками A и B. Обозначим точку пересечения прямой O1O2 с хордой AB как F.
Рассмотрим треугольники O1AO2 и O1BO2.
3) O1O2 — общая сторона.
Из равенства треугольников следует равенство соответствующих углов: ∠AO1F=BO1F, то есть O1F- биссектриса угла AO1B.
Треугольник AO1B — равнобедренный с основанием AB (O1A=O1B=R). Следовательно, биссектриса O1F является также его высотой и медианой. Таким образом,
Аналогично доказывается, что
По теореме о существовании и единственности прямой, перпендикулярной данной,через точку F можно провести только одну прямую, перпендикулярную данной прямой AB.
Следовательно, центры окружностей O1, O2 и точка F лежат на одной прямой O1O2, а общая хорда окружностей перпендикулярна этой прямой:
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Хорда, секущая, касательная
- Определения
- Свойства
- 🔍 Видео
Видео:Теорема о числе точек пересечения двух окружностейСкачать
Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Видео:Геометрия Общая хорда двух пересекающихся окружностей видна из их центров под углами 90 и 60. НайтиСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
| ||||
| Внутренняя касательная к двум окружностям | ||||
| ||||
| Общая хорда двух пересекающихся окружностей | ||||
| ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
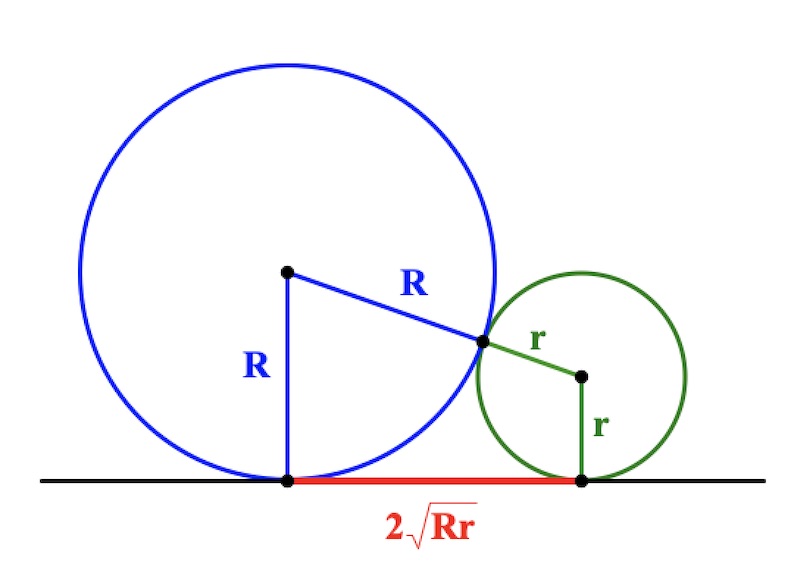
Длина общей хорды двух окружностей вычисляется по формуле
Видео:Свойство хорд, пересекающихся внутри окружностиСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Теорема о произведении отрезков пересекающихся хорд.Скачать  Хорда, секущая, касательнаяВидео:Геометрия В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимноСкачать  ОпределенияХорда – отрезок, соединяющий две точки окружности. В частности, хорда, проходящая через центр окружности, называется диаметром . Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках. Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать  Свойства
Радиус, проведенный в точку касания, перпендикулярен касательной
Отрезки касательных, проведенных к окружности из одной точки, равны.
Отрезки пересекающихся хорд связаны соотношением:
Произведения отрезков секущих, проведенных из одной точки, равны:
Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки: Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов Видеодоказательство
Чтобы не потерять страничку, вы можете сохранить ее у себя: 🔍 ВидеоЗадание 24 Две пересекающиеся окружностиСкачать 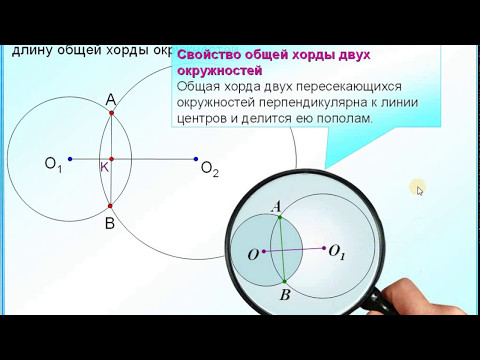 Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать  Теорема о секущей и касательной, о секущих, о пересекающихся хордах | Теоремы об окружностях - 1Скачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  #207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать  Алгоритмы. Пересечение окружностейСкачать  Взаимное расположение окружностей. Точки пересечения окружностейСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Математика Радиусы двух пересекающихся окружностей равны 17 см и 39 см, а расстояние между ихСкачать  Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать  Общая хорда двух окружностейСкачать  Пересечение двух окружностейСкачать  Теорема об отрезках хорд и секущихСкачать  |
