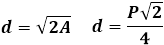Дан правильный четырехугольник найдите его диагональ если его сторона 8 корней из 2

Вопрос по математике:

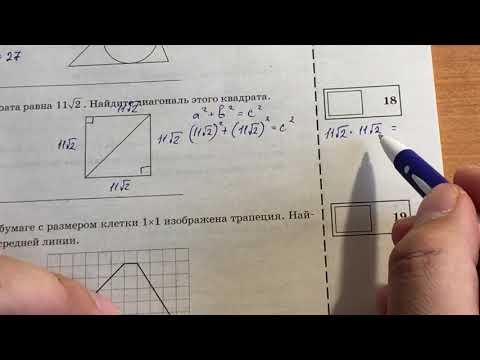
Сторона квадрата равна 8 под корнем из 2 . Найдите диагональ этого квадрата.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Длина диагонали по теореме Пифагора равна L=√(a²+a²)=√(2*64*2)=√256=16 единиц.

Ответ: 16 единиц.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Диагональ квадрата

Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.

Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
— Все стороны квадрата равны (от ромба)
— Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)

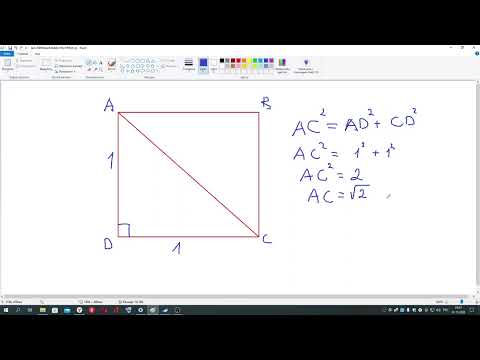
Если провести диагональ квадрата, то она образует с его сторонами не просто прямоугольный треугольник (как в прямоугольнике), но равнобедренный прямоугольный треугольник, который по теореме Пифагора будет связывать всего два параметра — диагональ квадрата и его сторону. Стороны квадрата будут катетами для треугольника, а диагональ гипотенузой.

a 2 +b 2 =c 2
a 2 +b 2 =d 2
2a 2 =d 2

Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:

Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.

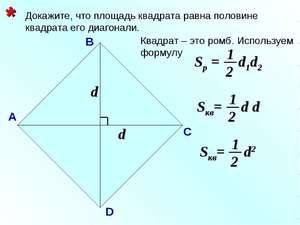
Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.

Формулы диагонали квадрата через площадь, периметр

Видео:№494. Найдите диагональ и площадь ромба, если его сторона равна 10 см, а другая диагональ — 12 см.Скачать

Формулы и способы как находить диагональ квадрата

При решении задач по школьной математике часто требуется определить, чему равняется диагональ заданного квадрата. При кажущейся некоторой сложности, эта задача является весьма простой и имеет несколько несложных способов решения. Рассмотрим их, для начала введём некоторые понятия и определения.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Определения и соглашения

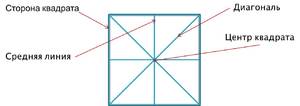
1. Квадрат — это четырёхугольник с равными сторонами, все углы которого являются прямыми, то есть равны 90 градусов. Данная фигура одновременно и ромб, и прямоугольник, поэтому сохраняет все их свойства.
2. Диагональ многоугольника — это отрезок, соединяющий две его противоположные вершины. В статье её будем обозначать буквой d.
3. Противоположными называются вершины, не лежащие на одной стороне.
4. Корень квадратный из числа, это такое число, которое при умножении само на себя даст исходное. В геометрии используются только положительные значения квадратного корня. В статье его будем обозначать сокращением rad (от латинского radical — корень).
5. Сторону квадрата будем обозначать буквой a.

Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.

Видео:№188. Ребро куба равно а. Найдите диагональ куба.Скачать

Вычисление диагонали квадрата по известной стороне

Самым простым способом является вычисление диагонали, если известна сторона квадрата. Здесь действует широко известная теорема Пифагора для прямоугольных треугольников. Запишем эту формулу: c^2 = a^2+b^2.

Отметим, что в нашем случае диагональ квадрата есть гипотенуза треугольника с равными катетами. Перепишем формулу исходя из наших условий: d^2 = a^2+a^2. Преобразуем, получим: d^2 = 2*a^2. Следующим шагом извлечём квадратный корень, получится: d = rad2*a. Это и есть наша конечная формула.

Рассмотрим вычисление на примере. Пусть a = 64. Подставим наше значение в формулу. Получим d = 64*rad2. Это и есть ответ.

Видео:ПОДРОБНОЕ РЕШЕНИЕ ВОСЕМНАДЦАТОГО ЗАДАНИЯ ОГЭ МАТЕМАТИКА 2018Скачать

Вычисление диагонали квадрата по известной площади

Пусть нам дана площадь квадрата, её обозначают латинской буквой S, найдём его диагональ.

Используем свойства прямоугольника и запишем формулу его площади.

S = a*b. Перепишем для b = a. Получим: s = a^2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS.

Пример: допустим, площадь равна 32 квадратных метра. Подставим это число. Получим rad2*rad32 = rad2*4*rad2 = 4*2 = 8 метров.

Видео:№493. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.Скачать

Вычисление диагонали по известному периметру

Пусть нам известен периметр. В дальнейшем его будем записывать латинской буквой P, найдём его d. Воспользуемся свойствами прямоугольника и запишем формулу его периметра.

P = два*(a + b). Перепишем для b = a. У нас получится: P = два*(a + a) = 2*2a = 4*a. Выразим из последней формулы сторону. Имеем: a = P/4. Воспользуемся тем, что: d = rad2*a. Выразим сторону через периметр. Наша формула примет видd = rad2*P/4.

Примере: пусть периметр равен 128 метров. Проведём несложный расчёт. Имеем, rad =d2*128/4 = 32*rad2 метров.

Видео:18 задание из ОГЭ. Найти диагональ квадратаСкачать

Вычисление по радиусу описанной и вписанной окружности

Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.

Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.

И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.

Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.

Видео:ЕГЭ Математика Задание 8#27103Скачать

Заключение

Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.

Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.

Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.

Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.

Видео:Задача: найти площадь квадрата если его диагональ ровна....Скачать

Видео

Из видео вы узнаете, как найти диагональ квадрата, если известна его площадь.

🎥 Видео

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Найти диагональ квадратаСкачать

Задание 3 ЕГЭ по математике. Урок 46Скачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

№449. Найдите площадь квадрата, если его сторона равна: а) 1,2 см; б) ¾ дм; в) 3√2 м.Скачать

Диагональ прямоугольника образует угол 50° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

10 класс, 24 урок, Прямоугольный параллелепипедСкачать

8 класс, 4 урок, ПараллелограммСкачать