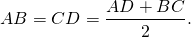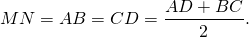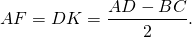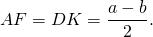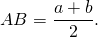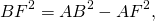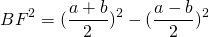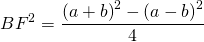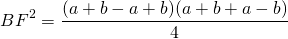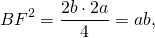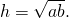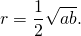Окружность вписана в равнобедренную трапецию основания которой равны 18

БАЗА ЗАДАНИЙ

Задание № 3. Планиметрия.

47. В треугольнике ABC CH — высота, AD — биссектриса, угол BAD=26°. Найдите угол AOC. Ответ дайте в градусах.

48. В треугольнике ABC угол B равен 45°, угол C равен 85°, AD — биссектриса, E— такая точка на AB, что AE=AC. Найдите угол BDE. Ответ дайте в градусах.

49. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE=CB. Найдите угол BDE.

50. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

51. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

52. Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

53. Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.

54. Углы треугольника относятся как 2 : 3 : 4. Найдите меньший из них. Ответ дайте в градусах.

55. Один острый угол прямоугольного треугольника в 4 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах.

56. Один угол равнобедренного треугольника на 90° больше другого. Найдите меньший угол. Ответ дайте в градусах.

57. Периметр прямоугольной трапеции, описанной около окружности, равен 40, её большая боковая сторона равна 11. Найдите радиус окружности.

58. Боковые стороны трапеции, описанной около окружности, равны 15 и 22. Найдите среднюю линию трапеции.

59. В четырёхугольник ABCD вписана окружность, AB=13, BC=7 и AD=11. Найдите четвёртую сторону четырёхугольника.

60. Два угла вписанного в окружность четырёхугольника равны 56° и 77°. Найдите меньший из оставшихся углов. Ответ дайте в градусах.

61. Окружность вписана в равнобедренную трапецию, основания которой равны 18 и 50. Прямая, проходящая через центр окружности и вершину D трапеции, отсекает от трапеции треугольник. Найдите отношение площади этого треугольника к площади трапеции.

62. Найдите вписанный угол, опирающийся на дугу, равную 1/5 окружности. Ответ дайте в градусах.

63. На окружности отмечены точки A, B и C. Дуга окружности AC, не содержащая точку B, составляет 200°. Дуга окружности BC, не содержащая точку A, составляет 80°. Найдите вписанный угол ACB. Ответ дайте в градусах.

64. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 82°, угол ABD равен 47°. Найдите угол CAD. Ответ дайте в градусах.

65. Четырёхугольник ABCD вписан в окружность. Угол CAD равен 32°, угол ABD равен 57°. Найдите угол ABC. Ответ дайте в градусах.

66. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

67. Найдите хорду, на которую опирается угол равный 30°, вписанный в окружность радиуса 3.

68. Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

69. Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную √2. Ответ дайте в градусах.

70. Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную √2. Ответ дайте в градусах.

71. Найдите хорду, на которую опирается угол 120, вписанный в окружность радиуса √3.

72. Хорда AB делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки C? Ответ дайте в градусах.

73. Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:3:5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

74. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95°, 49°, 71°, 145°. Найдите угол B этого четырехугольника. Ответ дайте в градусах.

75. Сторона правильного треугольника равна √3. Найдите радиус окружности, описанной около этого треугольника.

76. Радиус окружности, описанной около правильного треугольника, равен 38√3. Найдите сторону этого треугольника.

77. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 114°. Найдите вписанный угол ACB. Ответ дайте в градусах.

78. Угол ACB равен 54°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 138°. Найдите угол DAE. Ответ дайте в градусах.

79. Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна 58°. Найдите угол ACB. Ответ дайте в градусах.

80. Угол ACO равен 28°. Его сторона CA касается окружности с центром в точке O. Сторона CO пересекает окружность в точках B и D. Найдите градусную меру дуги AD окружности, заключённой внутри этого угла. Ответ дайте в градусах.

81. Найдите периметр прямоугольника, если его площадь равна 270, а отношение соседних сторон равно 2 : 15.

82. Периметр прямоугольника равен 76, а площадь 192. Найдите большую сторону прямоугольника.

83. Периметр прямоугольника равен 26, а диагональ равна 12. Найдите площадь этого прямоугольника.

84. Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.

85. Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.

Видео:В равнобедренную трапецию, периметр которой равен 180, а площадьравна 1620, можно вписать...Скачать

В равнобедренную трапецию, основания которой равны 18см и 6см, вписан круг?

Геометрия | 5 — 9 классы

В равнобедренную трапецию, основания которой равны 18см и 6см, вписан круг.

Найдите радиус этого круга и углы трапеции.

Окружность получилась не вписанная, но как получилось.

Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

В равнобедренную трапецию с основаниями 18 см и 6 см вписан круг?

В равнобедренную трапецию с основаниями 18 см и 6 см вписан круг.

Найдите его радиус и углы трапеции.

Видео:Планиметрия 38 | mathus.ru | окружность вписана в равнобедрунную трапецию | отношение площадейСкачать

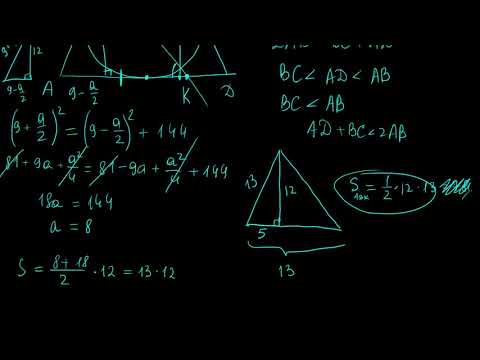
В равнобедренную трапецию вписана окружность радиуса 12 см, боковая сторона трапеции равна 25 см?

В равнобедренную трапецию вписана окружность радиуса 12 см, боковая сторона трапеции равна 25 см.

Найдите площадь трапеции!

Видео:Задание 18 Описанная трапецияСкачать

Около круга радиуса 3 описана равнобедренная трапеция с острым углом 60 градусов?

Около круга радиуса 3 описана равнобедренная трапеция с острым углом 60 градусов.

Найдите длину средней линии трапеции.

Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Периметр равнобедренной трапеции , описанной около круга радиуса 4, равен 40?

Периметр равнобедренной трапеции , описанной около круга радиуса 4, равен 40.

Найдите длину меньшего основания трапеции.

Видео:Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать

Найдите среднюю линию прямоугольной трапеции, в которой большая боковая сторона равна 10 см, а радиус вписанного круга равен 3 см?

Найдите среднюю линию прямоугольной трапеции, в которой большая боковая сторона равна 10 см, а радиус вписанного круга равен 3 см.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

В равнобедренной трапециии центр вписанного круга находится от вершины верхнего основания на расстоянии 3, а от вершины нижнего основания на 4?

В равнобедренной трапециии центр вписанного круга находится от вершины верхнего основания на расстоянии 3, а от вершины нижнего основания на 4.

Чему равна площадь круга, вписанная в трапецию?

Видео:🔴 В прямоугольной трапеции основания ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Задача : Диагонали равнобедренной трапеции делят среднюю линию на три равные отрезки?

Задача : Диагонали равнобедренной трапеции делят среднюю линию на три равные отрезки.

Найдите боковую сторону трапеции, если её меньшая основа равняется 7 см и в трапецию можно вписать круг.

Видео:Радиус описанной окружности трапецииСкачать

Помогите, Очень нужно?

Помогите, Очень нужно!

Боковая сторона равнобедренной трапеции равна 3 см.

Найдите площадь вписанного в него круга, если площадь трапеции равна 6 см ^ 2.

Видео:Задача про трапецию, описанную около окружностиСкачать

Площадь равнобедренной трапеции, описанной около круга, равна 8 см2, а острый угол трапеции равен 30?

Площадь равнобедренной трапеции, описанной около круга, равна 8 см2, а острый угол трапеции равен 30.

Найдите радиус вписанного круга.

Помогите очень надо!

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

7. Длина круга, вписанного в прямоугольную трапецию, равна 24π см?

7. Длина круга, вписанного в прямоугольную трапецию, равна 24π см.

Вычислите площадь трапеции, если ее нижнее основание на 10 см больше верхней.

На странице вопроса В равнобедренную трапецию, основания которой равны 18см и 6см, вписан круг? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Видео:Как доказать У равнобедренной трапеции углы при основаниях равны и диагонали равныСкачать

Вписанная в равнобедренную трапецию окружность

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.

Если MN —

3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.

По свойству равнобедренной трапеции,

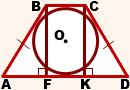
Из прямоугольного треугольника ABF по теореме Пифагора

4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство

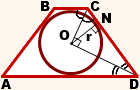
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

🎬 Видео

Окружность, вписанная в трапециюСкачать

Задание 26 Равнобедренная трапеция Окружности, вписанные в треугольникиСкачать

🔴 Основания трапеции равны 8 и 16, боковая сторона ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

№518. Найдите площадь равнобедренной трапеции, если: а) ее меньшее основание равно 18 см, высотаСкачать

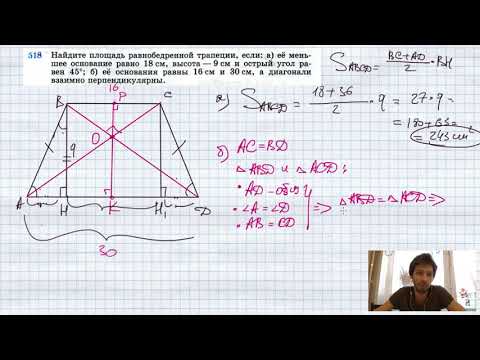
Всегда ли трапеция вписанная в окружность РАВНОБЕДРЕННАЯ? Задача. ЕГЭ, ОГЭ.Скачать

ГЕОМЕТРИЧЕСКАЯ задача ТИП 23 / ОГЭ #311560 / развернутая частьСкачать

ОГЭ задачи про трапецию. Решу ОГЭ, Ященко. Задания 16, 18Скачать