Дан параллелепипед найти координаты вектора (3 видео)

Содержание

Как найти координаты вектора в базисе
Координаты вектора в данном базисе.
Смешанное, векторное и скалярное произведение векторов
🎥 Видео

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Как найти координаты вектора в базисе

Решение:
Записываем матрицу перехода А:

и находим ее определитель
0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁ , f₂ , f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:

Обратная матрица А -1

Находим координаты вектора х относительно нового базиса.

Пример №1 . Даны векторы a, b, c и d . Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c

Пример №2 . Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Пример №3 . Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х»₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х»₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х»₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х»₁, x»₂, x»₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х»₁ = — x’₁ + 3x’₂ — 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х»₂ = — 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х»₃ = 3x’₁ — 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

A =

4	3	5
6	7	1
9	1	8

B =

-1	3	-2
-4	1	2
3	-4	5

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .

A -1 = -1/182

55	-19	-32
-39	-13	26
-57	23	10

Матрицу Х ищем по формуле:

X = A -1 ·B = -1/182

55	-19	-32
-39	-13	26
-57	23	10

-1	3	-2
-4	1	2
3	-4	5

75 /₁₈₂	-1 46 /₉₁	1 9 /₁₃
-13 /₁₄	1 2 /₇	-1
5 /₁₈₂	1 3 /₉₁	-1 2 /₁₃

Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e ₁= AB , e ₂= AC , e ₃= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e ₁, e ₂, e ₃)

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.

Видео:№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

Координаты вектора в данном базисе.

Дата добавления: 2015-08-06 ; просмотров: 9211 ; Нарушение авторских прав

Базисом векторного пространства называется такая упорядоченная линейно независимая система векторов, что любой вектор пространства можно представить в виде линейной комбинации векторов этой системы.

В трехмерном векторном пространстве базис состоит из трех векторов, который обычно обозначается так: <е₁, е₂, е₃ >.

Базис называется ортонормированным, если длины всех базисных векторов равны единицы, и базисные векторы попарно перпендикулярны. Ортонормированный базис обычно обозначается так: <i, j, k>.

Координатами вектора m в базисе <е₁, е₂, е₃ >называются коэффициенты разложения вектора m по векторам базиса, т.е. если m = хе₁ + уе₂ + zе₃, то числа х, у, z — координаты вектора m. В этом случае будем записывать m(х, у, z).

Имеет место теорема о координатах линейной комбинации:

1.24. Даны векторы а(2, 3, -1), b (0,1,4), с(1,0,-3). Найти координаты векторов: а) 2а — b —2с,б)а — b —3с,в)а +2b +3с),г) а — b – с,

д) 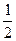( а + b), е) (а — 2 b + с).

ОТВЕТ. а) (2,5,0), б) (-1,2,4), в) (5,5,-2), г) (1,2,-2), д) (1,1,3), е) (1, ,-4)

ПРИМЕР 1.7

Даны векторы а(1,1,2), b (-2, 3 5), с(-4,1,1), d (0, -1, 3) Можно ли вектор dпредставить в виде линейной комбинации векторов а, b, с? Если да, то найти коэффициенты этой линейной комбинации.

Выясним, существуют ли такие числи х, у, z, что

d =ха +уb +z с.(1)

По теореме о координатах линейной комбинации векторов из равенства (1) получаем выражение для первой координаты вектора dчерез первые координаты векторов а, b, с, и аналогичные выражения для вторых и третьих координат

0 = х — 2у — 4 z (2)

Выясним, имеет ли эта система решение. Из (2) следует, что

Затем, подставляя (5) в (3) и (4), получаем:

Система, состоящая из уравнений (2), (3), (4), равносильна системе, состоящей из уравнений (5), (6), (7) . Ясно, что последняя система не имеет решений, следовательно, и данная система не имеет решений,. Поэтому вектор dнельзяпредставить в виде линейной комбинации векторов а, b, с. ■

1.25. Определить, какие из данных троек векторов линейно зависимы:

а) а(-3,0, 2), b (2, 1, -4), с(11, -2, -2); б) а(1, 0, 7), b (-1, 2, 4), с(3, 2, 1);

в) а(5, -1,4),b (3,-5, 2), с(-1,-13, -2).

ОТВЕТ.. а), с) линейно зависимы.

1.26. Представить вектор d как линейную комбинацию векторов а, b, с:

1)а(2,3,1), b (5, 7, 0), с(3, -2, 4), d (4, 12, -3);

2) а(5, -2, 0), b (0, -3, 4), с(-6, 0, 1), d (25, -22, 16);

3)а(3, 5, 6), b (2, -7, 1), с(12, 0, 6), d (0, 20, 18).

ОТВЕТ. 1) d = а + b + с, 2) d = 5а + 4b, 3) d = 4а – с.

1.27. Можно ли вектор d (1,1,1) представить в виде линейной комбинации векторов а(1,-1,0), b (2,2,1), с(0,-4,-1)?

ОТВЕТ.. Нет.

1.28. Даны векторы а(х, 3, 4), b (-1, 5, у).Существуют ли такие числа х и у, для которых система векторов <а, b >линейно зависима ?

ОТВЕТ. Да, х = — , у = .

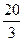
ПРИМЕР 1.8

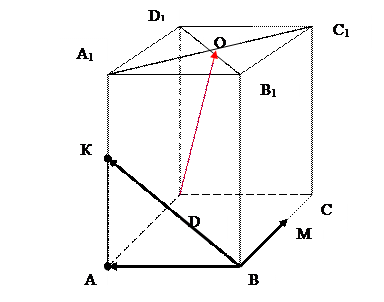
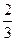
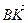
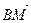
В параллелепипеде АВСDА₁В₁С₁D₁ К – середина ребра АА₁, точка М лежит на ребре ВС и ВМ = ВС, О = А₁С₁ В₁D₁. Найти координаты вектора в базисе < , , > .

Так как координаты вектора в данном базисе это коэффициенты разложения этого вектора по векторам базиса, то данную задачу можно сформулировать так: выразить вектор через векторы , , ,поэтому будем действовать так же, как при решении ПРИМЕРА 1.3.

1) = + = + = 2 + , т.е.

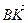
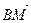
=2 + . (1).

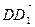
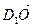
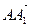
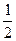
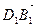
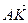
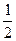
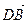
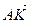
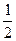
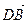
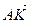
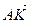
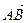
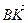
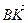
2) Выразим вектор через базисные векторы.

= + = — + .(2)

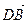
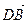
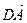
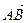
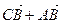
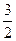
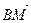
3) Выразим вектор через базисные векторы.

= + = = — – (3)

4) Подставим (2) и (3) в (1), получим

= 2(— + ) + (- – ) = 2– – .

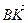
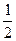
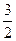
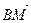
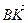
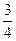
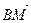
Следовательно, первая координата вектора равна 2, вторая координата равна — , третья координата равна — , т.е. (2, — , — ).

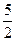
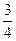
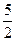
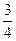
ОТВЕТ. (2, — , — ).

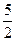
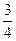
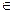
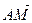
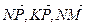
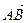
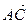
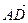
1.29. АВСD – тетраэдр. М и К – точки пересечения медиан граней ВСD и АDС, N – середина АВ, Р ВС и ВР : РС = 1 :2. Найти координаты векторов , в базисе < , , > .

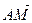
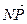
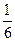
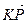
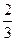
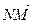
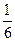
ОТВЕТ. ( , , ), ( , , 0), ( ,0, — ), (- , , ).

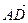
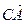
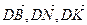
1.30. АВСD – тетраэдр. N и К середины ребер ВС и АС. Найти координаты векторов и в базисе < > .

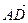
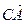
ОТВЕТ. (-1,2,-2), (2,-4,2).

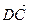
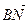
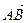
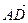
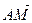
1.31. В тетраэдре АВСD М- середина ВС, а N – точка пересечения медиан грани АDС. Найти координаты векторов и в базисе < , , >.

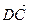
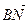
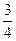
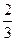
ОТВЕТ. (-1,-1,2), (- , , ).

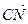
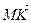
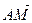
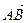
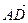
1.32. В тетраэдре АВСD N — середина ВС, а М и К – точки пересечения медиан граней ВСD и АВD. Найти координаты векторов и в базисе < , , >.

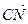
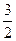
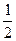
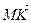
ОТВЕТ. (- , 1, ), (-1, , ).

Видео:№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Смешанное, векторное и скалярное произведение векторов

Задача:

Дан параллелепипед ABCDA₁B₁C₁D₁, построен на векторах AB(4,3,0), AD(2,1,2) и AA₁(-3,-2,5).
Найти:

Решение:

а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA₁). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.

(AB AD AA₁)

4	3	0
2	1	2
-3	-2	5

20 — 18 + 0 — 0 — 30 + 16

-12

Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
V_{ABCDA₁B₁C₁D₁}=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. S_ABCD= |[AB AD]|.

[AB AD]

i	j	k
4	3	0
2	1	2

6i — 8j — 2k

Теперь найдём модуль этого вектора:

S_ABCD= \|[AB AD]\|=√	(36+64+4)	=2√(26).

[AD AA₁]

i	j	k
2	1	2
-3	-2	5

9i — 16j — k

S_ADD₁A₁= |[AD AA₁]|=√(81+256+1)=13√2.

в) Что бы найти длину высоты, проведенной из вершины A₁ на грань ABCD, используем формулу для нахождения объема параллелепипеда V=h S_ABCD. С этой формулы видим:

V
S_ABCD

12
2√(26)

6
√(26)

3√(26)
13

г) Косинус угла λ₁, между ребром AB и диагональю B₁D будем высчитывать с помощью скалярного произведения векторов

cos(λ₁)

(AB B₁D)
\|AB\| * \|B₁D\|

Координаты вектора AB мы имеем, от вектор B₁D надо найти. Для этого используем следующую формулу:
B₁D = B₁A₁ + A₁A + AD = — AB — AA₁ + AD₁ = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B₁D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B₁D:
|AB|=√(16+9+0)=5, |B₁D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B₁D, (AB B₁D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:

cos(λ₁)

4
5√(10)

2√(10)
25

д) Что бы найти cos(λ₂), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD₁A₁ мы можем взять вектор [AD AA₁], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.

cos(λ₂)

69 + (-8)(-16) + (-2)*(-1)
2√(26) * 13√(2)

46√(13)
169

Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD₁A₁.

🎥 Видео

Координаты точки и координаты вектора 1.Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

11 класс, 2 урок, Координаты вектораСкачать

Координаты вектора. 9 класс.Скачать

Координаты в новом базисеСкачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

9 класс, 2 урок, Координаты вектораСкачать

Правило параллелепипеда для векторовСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

§20 Нахождение объёма параллелипипедаСкачать

координаты вектора AH, который перпендикуляр из точки A к основанию параллелепипедаСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

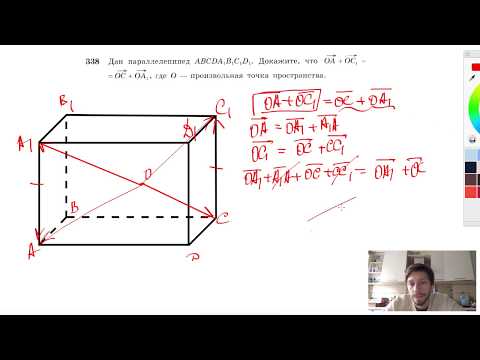
№338. Дан параллелепипед ABCDA1B1C1D1. Докажите, что OA + OC1=OC+OA1Скачать