Сторона остроугольного треугольника является диаметром окружности

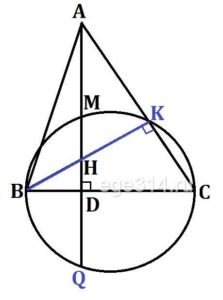
Задание 26. На стороне ВС остроугольного треугольника ABC (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту AD в точке М, AD = 80, MD = 64, Н — точка пересечения высот треугольника ABC. Найдите АН.

AD – высота треугольника ABC, значит, . Учитывая, что MQ – хорда, с которой радиус окружности составляет 90º, то точка D делит MQ пополам и MD=DQ=64.

AM = AD-MD = 80-64=16,

AQ = AD+DQ = 80+64 = 144

По следствию из теоремы о касательной и секущей, имеем:

Треугольники AKH и ADC подобны по двум углам: , а угол CAD – общий. Следовательно,

Видео:Геометрия. Задача. Треугольник. Окружность.Скачать

Решение №1223 На стороне ВС остроугольного треугольника АВС (АВ ≠ АС) как на диаметре построена полуокружность …

На стороне ВС остроугольного треугольника АВС (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту АD в точке М, АВ = 80‚ МD = 64, Н – точка пересечения высот треугольника АВС. Найдите АН.

Источник: ОГЭ 2021 Ященко (36 вар)

Построим высоту BK, ВК⊥АС, ΔВKC прямоугольный и опирается на диаметр окружности, значит точка К лежит на окружности.
MQ – хорда окружности, диаметр ВС⊥MQ, значит хорда делится пополам в точке D:

MD = DQ = 64

Найдём АМ:

AM = AD – MD = 80 – 64 = 16

Найдём AQ:

AQ = AD + DQ = 80 + 64 = 144

По теореме о секущих:

AK·AC = AM·AQ
AK·AC = 16·144

ΔAKH и ΔADC подобны по двум углам: ∠AKH = ∠ADC = 90°, а ∠CAD – общий. Тогда стороны тоже подобны:

Видео:Геометрия Сторона AD четырехугольника ABCD является диаметром окружности, описанной около негоСкачать

Треугольник вписанный в окружность

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:ОГЭ задание 26Скачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

💥 Видео

ОГЭ 2021. Задание 24. Геометрическая задача на вычисление.Скачать

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Геометрия. ОГЭ по математике. Задание 15Скачать

Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

ОГЭ без рекламы математика вариант 9 и 10 задача 25Скачать

Треугольник и окружность // ФАКТ ДЛЯ ОГЭСкачать

№707. Угол, противолежащий основанию равнобедренного треугольника, равен 120°, боковая сторонаСкачать

На катете ML прямоугольного треугольника KLM как на диаметре построена окружностьСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Геометрия На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построенаСкачать

Треугольник и окружность #shortsСкачать

Угол между биссектрисами острых углов прямоугольного треугольникаСкачать