Скачать
презентацию
Упражнение 6. Докажите, что прямые AB и C1D1, проходящие через вершины куба ABCDA1B1C1D1, параллельны. Доказательство: Прямые AB и C1D1 параллельны прямой CD, так как грани ABCD и CDD1C1 – квадраты. Из транзитивности отношения параллельности следует, что прямые AB и C1D1 параллельны.
Слайд 7 из презентации «Параллельность прямых в пространстве» к урокам геометрии на тему «Параллельность в пространстве»
Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке геометрии, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Параллельность прямых в пространстве.ppt» можно в zip-архиве размером 177 КБ.
- Параллельность в пространстве
- Параллельность прямой плоскости
- Просмотр содержимого документа «Параллельность прямой плоскости»
- Презентация по теме Перпендикулярность прямых и плоскостей
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
- 📽️ Видео
Видео:№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

Параллельность в пространстве
«Теоремы о параллельности плоскостей и прямых» — Проведем плоскость. Плоскости не пересекаются. Теорема. Теорема о параллельных прямых. Точки прямой. Середина. Прямая, не лежащая в данной плоскости. Признак параллельности двух плоскостей. Параллельность прямых и плоскостей в пространстве. Прямые АВ и СD. Докажем единственность плоскости. Плоскость проходит через сторону АС.
«Параллельные прямые в пространстве» — Какие прямые в пространстве называются параллельными? Отрезки в пространстве называются параллельными, если … Лемма о параллельных прямых. Следствия аксиомы параллельных прямых — ? Вернемся в пространство. Параллельными называются прямые, лежащие в одной плоскости и не имеющие точек пересечения. Теорема о параллельных прямых.
«Параллельность в пространстве» — Возможны три случая взаимного расположения прямой и плоскости в пространстве: Прямая лежит в плоскости. Кроссворд. Свойства параллельных плоскостей. Параллельность в пространстве. Прямая и плоскость не имеют общих точек. Параллельные прямые в пространстве. Отрезки параллельных прямых, заключенных между параллельными плоскостями равны.
«Параллельные плоскости» — Стороны AB и BC параллелограмма ABCD пересекают некоторую плоскость. Прямая пересекает две стороны треугольника. Ввести понятие параллельных плоскостей. Теорема. Параллельные плоскости в пространстве. Взаимное расположение двух плоскостей в пространстве. Сформулировать и доказать признак параллельности плоскостей.
«Определение параллельности прямых» — Отрезки параллельных прямых. Взаимное расположение прямых. Свойство. Полуплоскости. Стороны. Скрещивающиеся прямые. Две параллельные плоскости. Плоскость. Признак параллельности. Одна из двух параллельных прямых пересекает плоскость. Параллельность плоскостей. Точка. Две прямые. Взаимное расположение.
«Параллельность прямых в пространстве» — Назовите прямые, проходящие через вершины куба. Ребра икосаэдра. Прямые, проходящие через вершины многогранника. N параллельных между собой прямых. Прямые AB и C1D1, проходящие через вершины куба ABCDA1B1C1D1, параллельны. Сколько имеется пар параллельных прямых, содержащих ребра октаэдра. Прямые AD и B1C1 параллельны.
Видео:№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Параллельность прямой плоскости
Параллельность прямой плоскости.10 класс Презентация составлена для изучения темы. Будет полезна учителям и учащимся.
Просмотр содержимого документа
«Параллельность прямой плоскости»
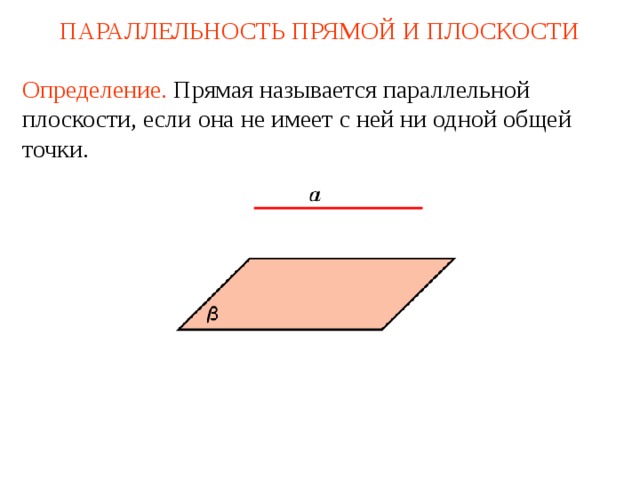
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Определение. Прямая называется параллельной плоскости, если она не имеет с ней ни одной общей точки.
В режиме слайдов формулировка появляется после кликанья мышкой
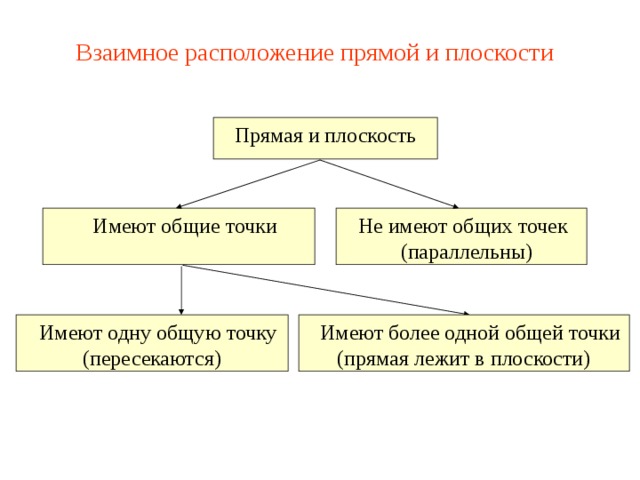
Взаимное расположение прямой и плоскости
Прямая и плоскость
Имеют общие точки
Не имеют общих точек
Имеют одну общую точку (пересекаются)
Имеют более одной общей точки (прямая лежит в плоскости)
Параллельности двух прямых
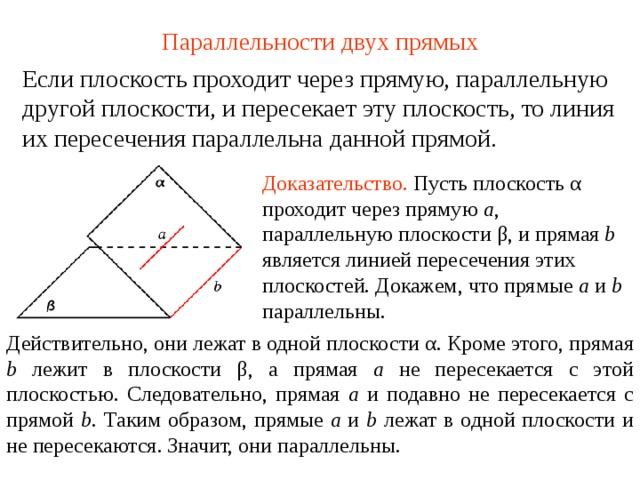
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия их пересечения параллельна данной прямой.
Доказательство. Пусть плоскость α проходит через прямую a , параллельную плоскости β , и прямая b является линией пересечения этих плоскостей. Докажем, что прямые a и b параллельны.
В режиме слайдов формулировка появляется после кликанья мышкой
Действительно, они лежат в одной плоскости α . Кроме этого, прямая b лежит в плоскости β , а прямая a не пересекается с этой плоскостью. Следовательно, прямая a и подавно не пересекается с прямой b . Таким образом, прямые a и b лежат в одной плоскости и не пересекаются. Значит, они параллельны.
Признак параллельности прямой и плоскости
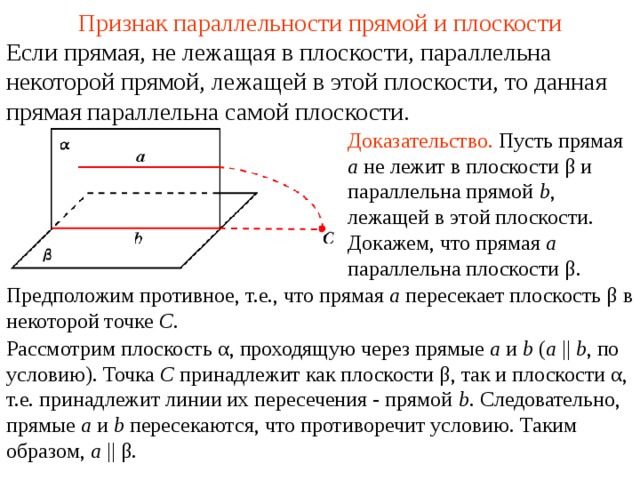
Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости.
Доказательство. Пусть прямая a не лежит в плоскости β и параллельна прямой b , лежащей в этой плоскости. Докажем, что прямая a параллельна плоскости β .
Предположим противное, т.е., что прямая a пересекает плоскость β в некоторой точке C .
В режиме слайдов формулировка появляется после кликанья мышкой
Рассмотрим плоскость α , проходящую через прямые a и b ( a || b , по условию). Точка C принадлежит как плоскости β , так и плоскости α , т.е. принадлежит линии их пересечения — прямой b . Следовательно, прямые a и b пересекаются, что противоречит условию. Таким образом, a || β .
Верно ли утверждение о том, что две прямые, параллельные одной и той же плоскости, параллельны между собой?
В режиме слайдов ответ появляется после кликанья мышкой
Верно ли утверждение: «Прямая, параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости»?
В режиме слайдов ответ появляется после кликанья мышкой
Одна из двух параллельных прямых параллельна плоскости. Верно ли утверждение, что и вторая прямая параллельна этой плоскости?
В режиме слайдов ответ появляется после кликанья мышкой
Даны две параллельные прямые. Через каждую из них проведена плоскость. Эти две плоскости пересекаются. Как расположена их линия пересечения относительно данных прямых?
В режиме слайдов ответ появляется после кликанья мышкой
Даны две пересекающиеся плоскости. Существует ли плоскость, пересекающая две данные плоскости по параллельным прямым?
В режиме слайдов ответ появляется после кликанья мышкой
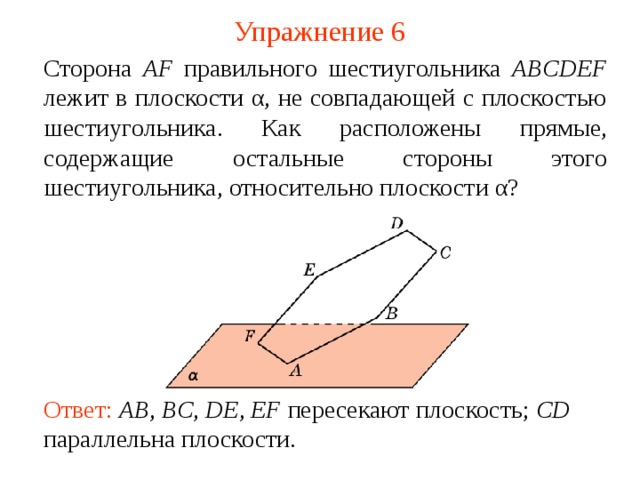
Сторона AF правильного шестиугольника ABCDEF лежит в плоскости α, не совпадающей с плоскостью шестиугольника. Как расположены прямые, содержащие остальные стороны этого шестиугольника, относительно плоскости α?
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: AB , BC , DE , EF пересекают плоскость; CD параллельна плоскости.
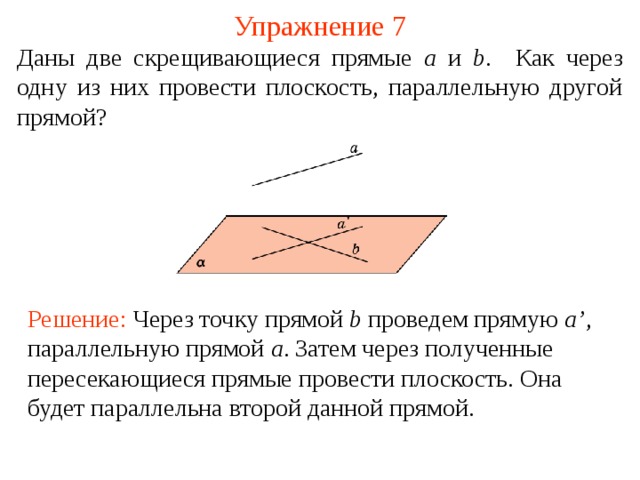
Даны две скрещивающиеся прямые a и b . Как через одну из них провести плоскость, параллельную другой прямой ?
Решение: Через точку прямой b проведем прямую a’ , параллельную прямой a . Затем через полученные пересекающиеся прямые провести плоскость. Она будет параллельна второй данной прямой.
В режиме слайдов ответ появляется после кликанья мышкой
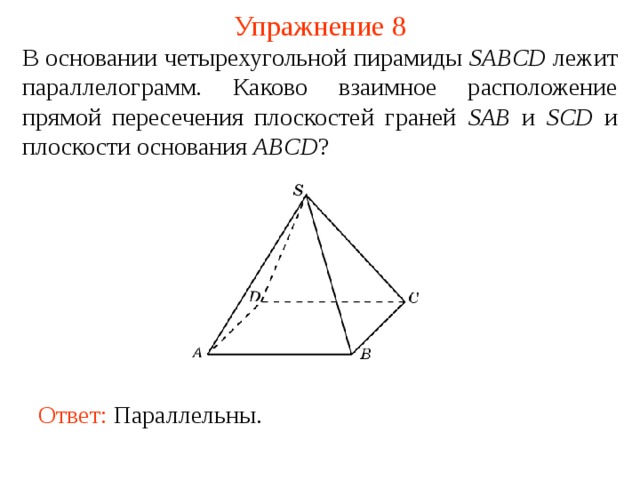
В основании четырехугольной пирамиды SABCD лежит параллелограмм. Каково взаимное расположение прямой пересечения плоскостей граней SAB и SCD и плоскости основания ABCD ?
В режиме слайдов ответ появляется после кликанья мышкой
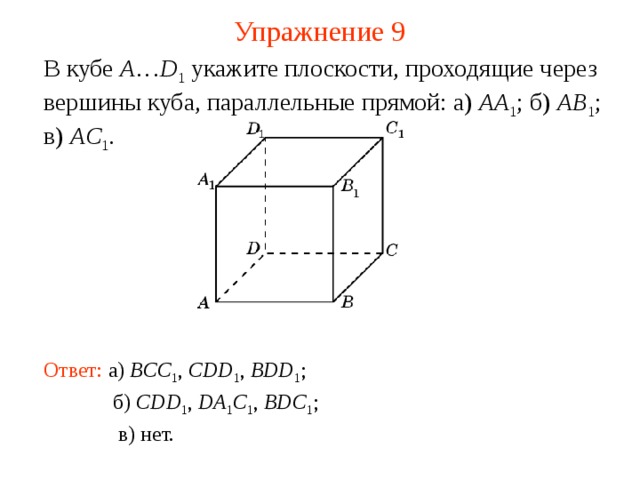
В кубе A … D 1 укажите плоскости, проходящие через вершины куба, параллельные прямой: а) AA 1 ; б) AB 1 ; в) AC 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: а ) BCC 1 , CDD 1 , BDD 1 ;
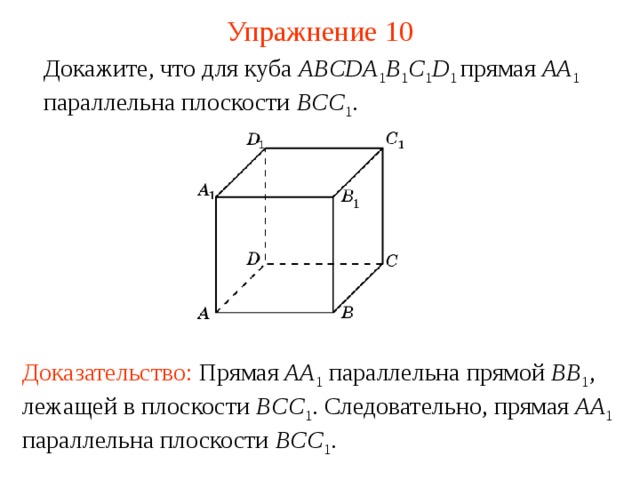
Докажите, что для куба ABCDA 1 B 1 C 1 D 1 прямая AA 1 параллельна плоскости BCC 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AA 1 параллельна прямой BB 1 , лежащей в плоскости BCC 1 . Следовательно, прямая AA 1 параллельна плоскости BCC 1 .
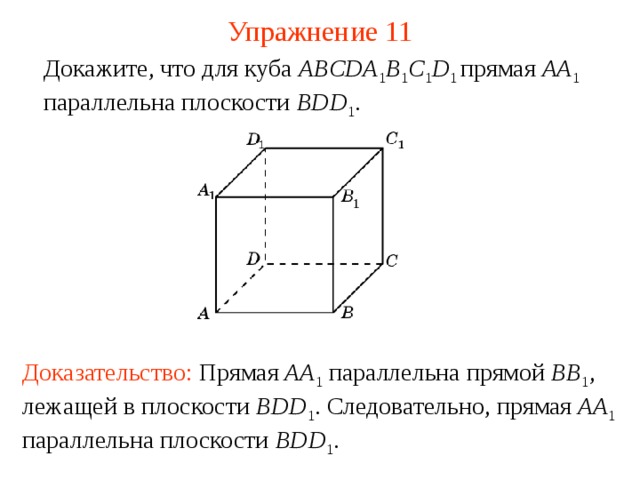
Докажите, что для куба ABCDA 1 B 1 C 1 D 1 прямая AA 1 параллельна плоскости BDD 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AA 1 параллельна прямой BB 1 , лежащей в плоскости BDD 1 . Следовательно, прямая AA 1 параллельна плоскости BDD 1 .
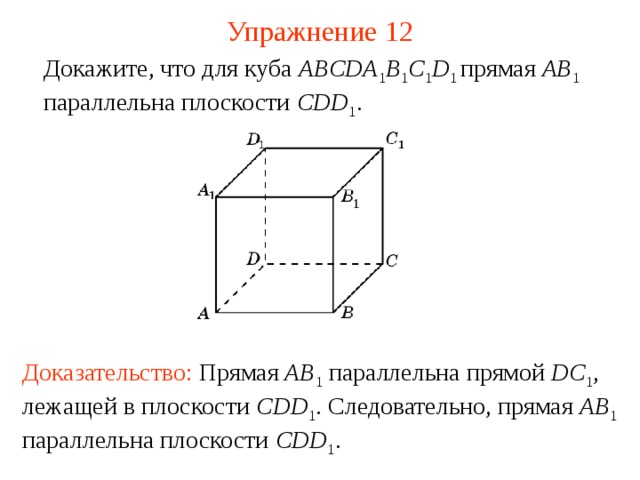
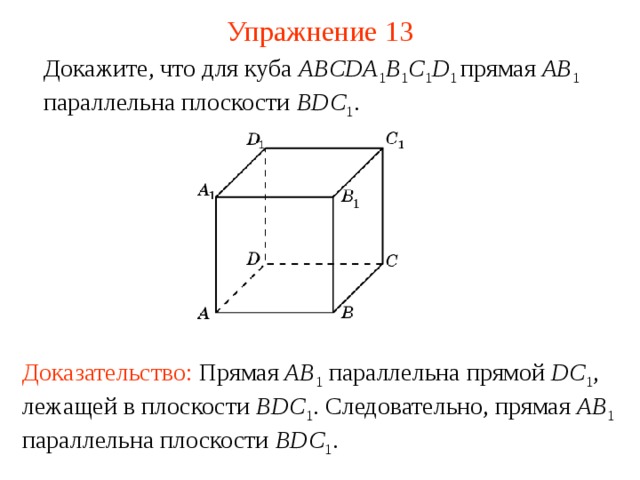
Докажите, что для куба ABCDA 1 B 1 C 1 D 1 прямая AB 1 параллельна плоскости CDD 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AB 1 параллельна прямой DC 1 , лежащей в плоскости CDD 1 . Следовательно, прямая AB 1 параллельна плоскости CDD 1 .
Докажите, что для куба ABCDA 1 B 1 C 1 D 1 прямая AB 1 параллельна плоскости BDC 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AB 1 параллельна прямой DC 1 , лежащей в плоскости BDC 1 . Следовательно, прямая AB 1 параллельна плоскости BDC 1 .
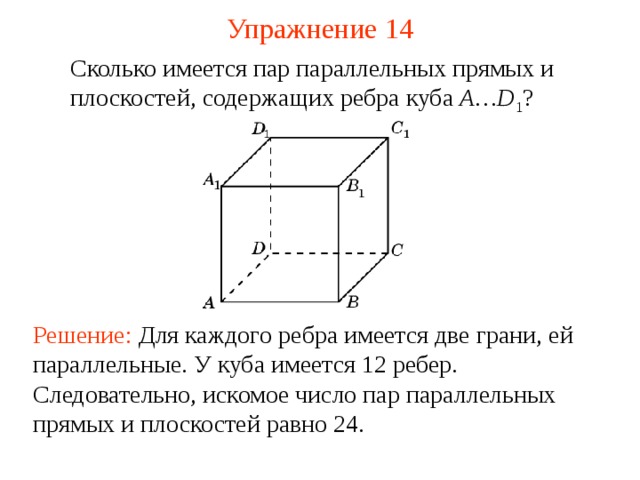
Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра куба A…D 1 ?
В режиме слайдов ответ появляется после кликанья мышкой
Решение: Для каждого ребра имеется две грани, ей параллельные. У куба имеется 12 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 24.
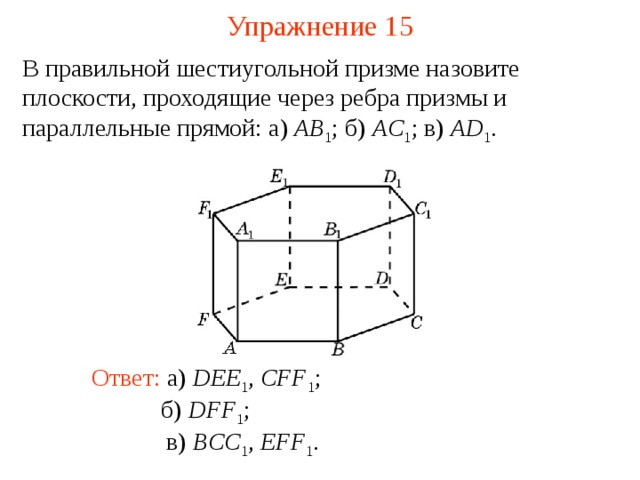
В правильной шестиугольной призме назовите плоскости, проходящие через ребра призмы и параллельные прямой: а) AB 1 ; б) AC 1 ; в) AD 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: а) DEE 1 , CFF 1 ;
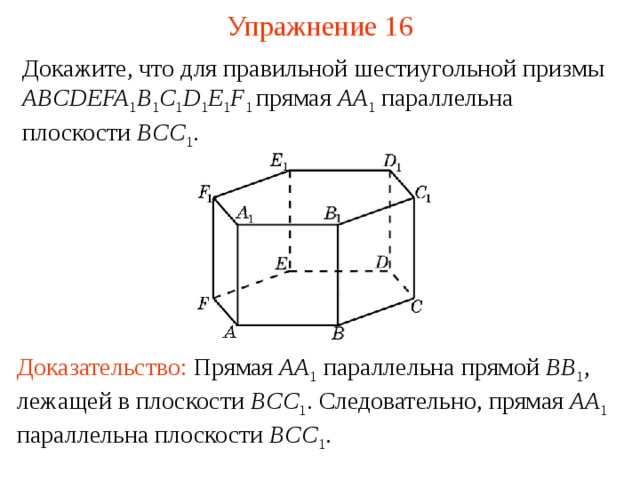
Докажите, что для правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 прямая AA 1 параллельна плоскости BCC 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AA 1 параллельна прямой BB 1 , лежащей в плоскости BCC 1 . Следовательно, прямая AA 1 параллельна плоскости BCC 1 .
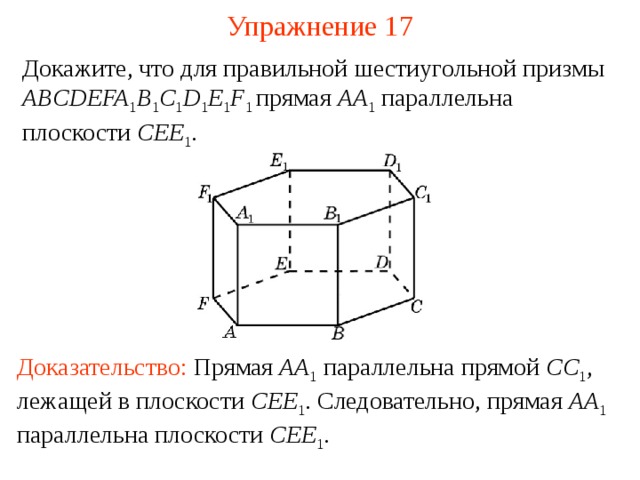
Докажите, что для правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 прямая AA 1 параллельна плоскости CEE 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AA 1 параллельна прямой CC 1 , лежащей в плоскости CEE 1 . Следовательно, прямая AA 1 параллельна плоскости CEE 1 .
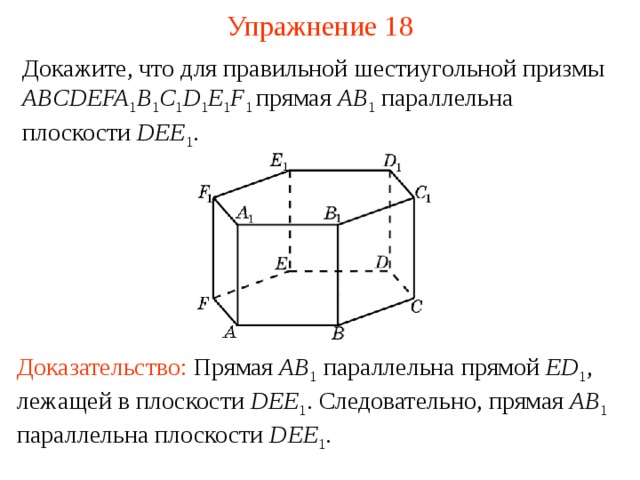
Докажите, что для правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 прямая AB 1 параллельна плоскости DEE 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AB 1 параллельна прямой ED 1 , лежащей в плоскости DEE 1 . Следовательно, прямая AB 1 параллельна плоскости DEE 1 .
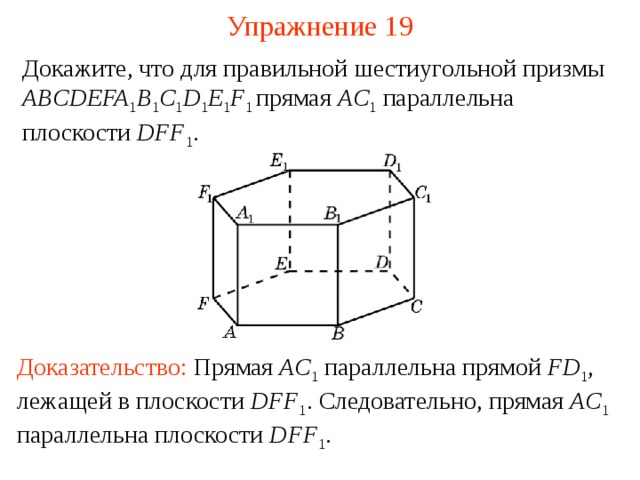
Докажите, что для правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 прямая AC 1 параллельна плоскости DFF 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AC 1 параллельна прямой FD 1 , лежащей в плоскости DFF 1 . Следовательно, прямая AC 1 параллельна плоскости DFF 1 .
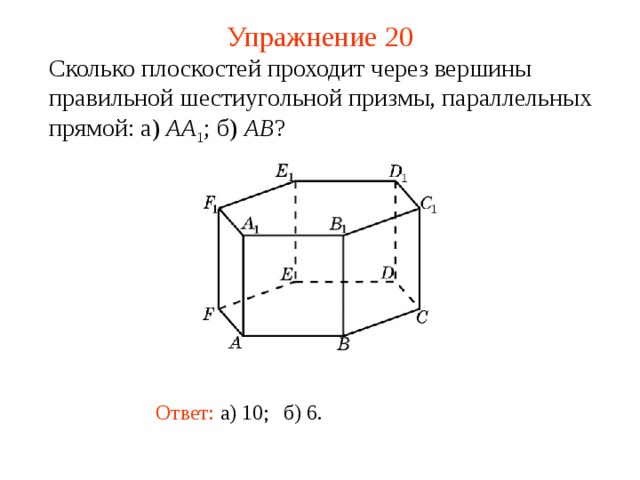
Сколько плоскостей проходит через вершины правильной шестиугольной призмы, параллельных прямой: а) AA 1 ; б) AB ?
В режиме слайдов ответ появляется после кликанья мышкой
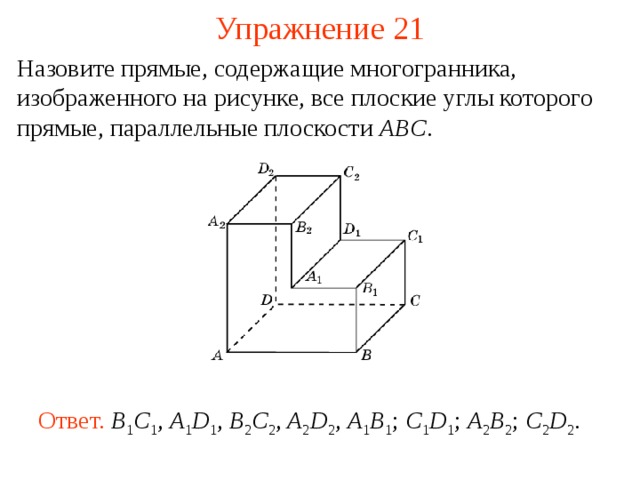
Назовите прямые, содержащие многогранника, изображенного на рисунке, все плоские углы которого прямые, параллельные плоскости ABC .
В режиме слайдов ответ появляется после кликанья мышкой
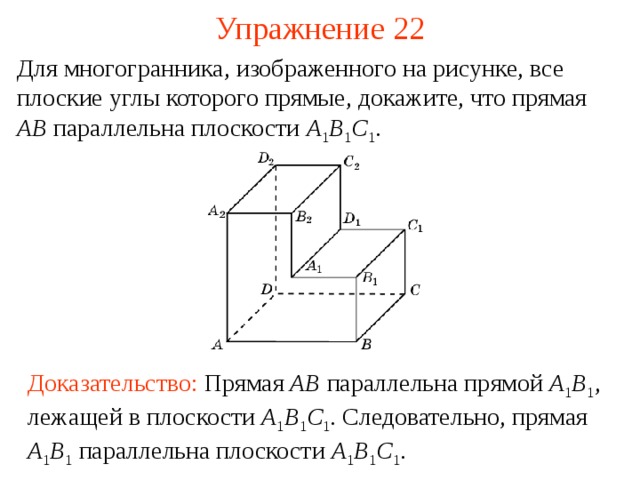
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AB параллельна плоскости A 1 B 1 C 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AB параллельна прямой A 1 B 1 , лежащей в плоскости A 1 B 1 C 1 . Следовательно, прямая A 1 B 1 параллельна плоскости A 1 B 1 C 1 .
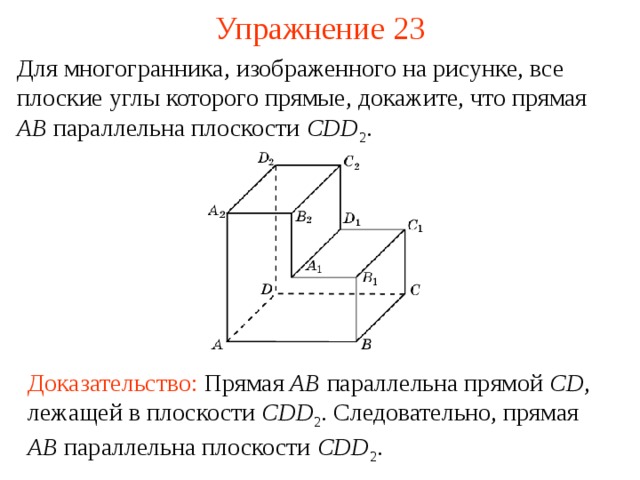
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AB параллельна плоскости CDD 2 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AB параллельна прямой CD , лежащей в плоскости CDD 2 . Следовательно, прямая AB параллельна плоскости CDD 2 .
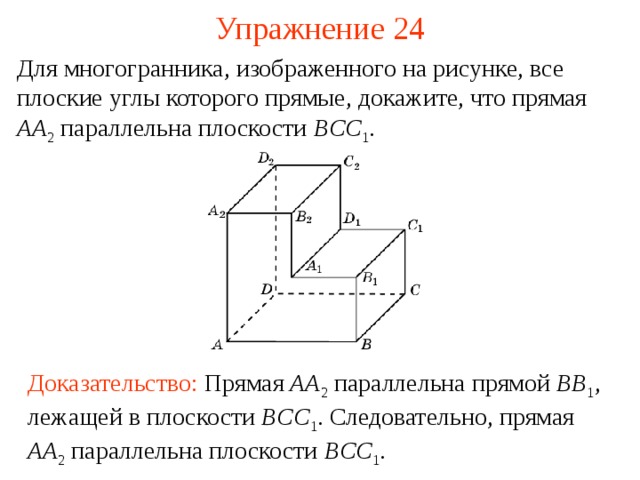
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AA 2 параллельна плоскости BCC 1 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AA 2 параллельна прямой BB 1 , лежащей в плоскости BCC 1 . Следовательно, прямая AA 2 параллельна плоскости BCC 1 .
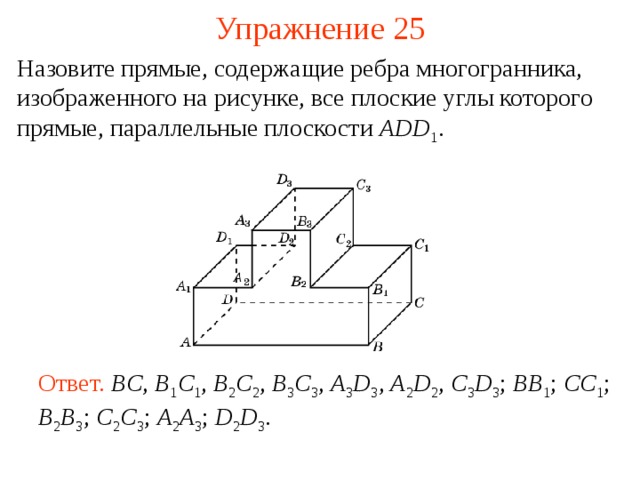
Назовите прямые, содержащие ребра многогранника, изображенного на рисунке, все плоские углы которого прямые, параллельные плоскости ADD 1 .
В режиме слайдов ответ появляется после кликанья мышкой
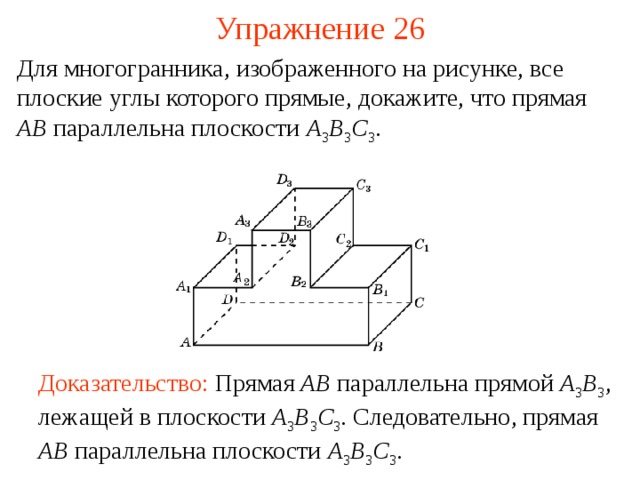
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AB параллельна плоскости A 3 B 3 C 3 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AB параллельна прямой A 3 B 3 , лежащей в плоскости A 3 B 3 C 3 . Следовательно, прямая AB параллельна плоскости A 3 B 3 C 3 .
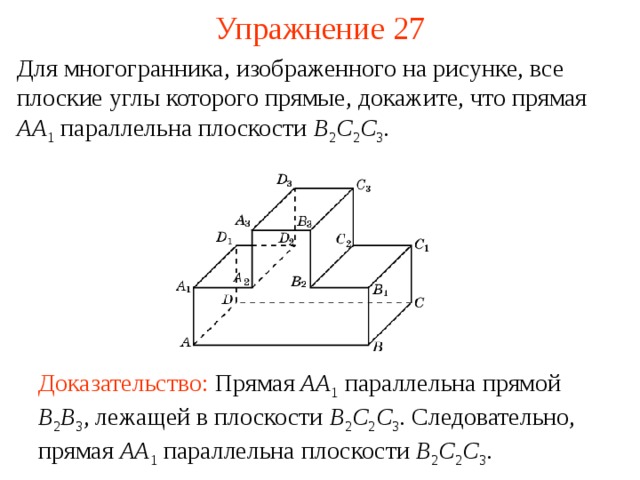
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AA 1 параллельна плоскости B 2 C 2 C 3 .
В режиме слайдов ответ появляется после кликанья мышкой
Доказательство: Прямая AA 1 параллельна прямой B 2 B 3 , лежащей в плоскости B 2 C 2 C 3 . Следовательно, прямая AA 1 параллельна плоскости B 2 C 2 C 3 .
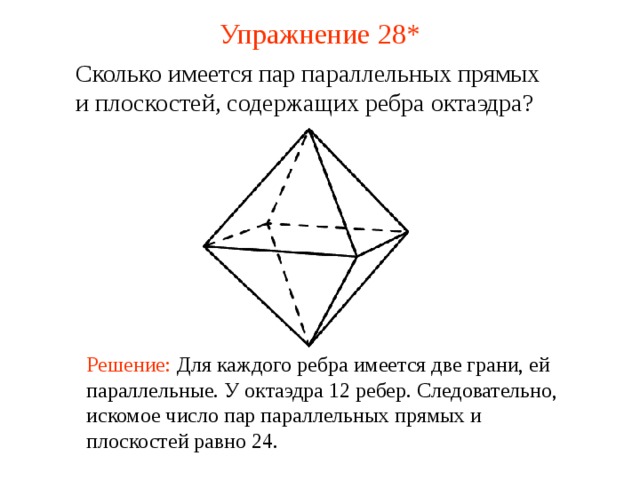
Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра октаэдра?
В режиме слайдов ответ появляется после кликанья мышкой
Решение: Для каждого ребра имеется две грани, ей параллельные. У октаэдра 12 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 24.
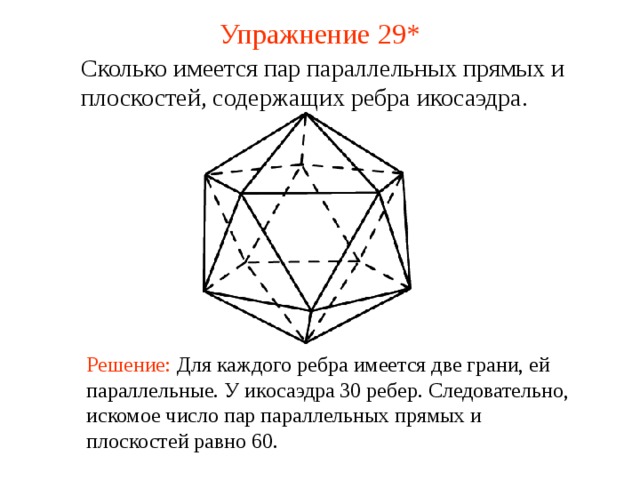
Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра икосаэдра .
В режиме слайдов ответ появляется после кликанья мышкой
Решение: Для каждого ребра имеется две грани, ей параллельные. У икосаэдра 30 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 60.
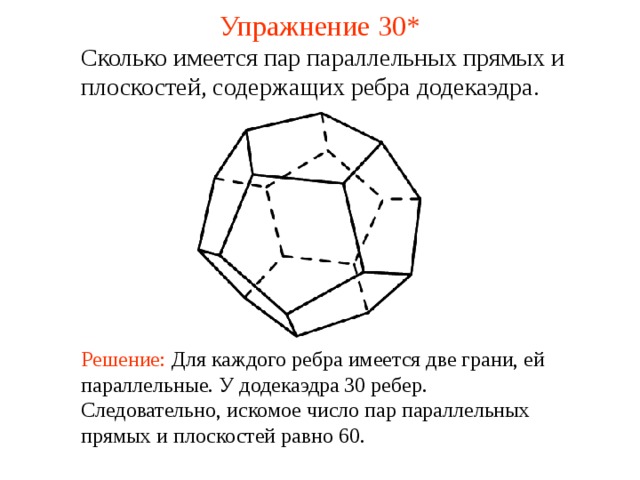
Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра додекаэдра .
В режиме слайдов ответ появляется после кликанья мышкой
Решение: Для каждого ребра имеется две грани, ей параллельные. У додекаэдра 30 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 60.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Презентация по теме Перпендикулярность прямых и плоскостей
Видео:№196. Изобразите куб ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через:Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Видео:№191. Дан куб ABCDA1B1C1D1. Докажите, что плоскостиСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
«Перпендикулярность прямых и плоскостей»
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ ДВУГРАННЫЙ УГОЛ РЕШЕНИЕ ЗАДАЧ План: *
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Теорема. (Признак перпендикулярности прямой и плоскости.) Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна и самой плоскости. *
Докажите, что плоскость, проходящая через ребро AB правильного тетраэдра ABCD и точку Е – середину ребра CD, перпендикулярна ребру CD. Упражнение 1 Доказательство: Прямая CD перпендикулярна прямым AE и BE. Следовательно, она перпендикулярна плоскости ABE. *
Докажите, что прямая AA1, проходящая через вершины куба ABCDA1B1C1D1 перпендикулярна плоскости ABC. Доказательство. Прямая AA1 перпендикулярна прямым AB и AD. Следовательно, она перпендикулярна плоскости ABC. Упражнение 2 *
ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ Пусть дана плоскость π и точка A пространства. Через точку A проведем прямую a, перпендикулярную плоскости π. Точку пересечения прямой a с плоскостью π обозначим A’. Она называется ортогональной проекцией точки A на плоскость π. Отрезок AA’ называется перпендикуляром, опущенным из точки A на плоскость π. *
ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ Наклонной к плоскости называется прямая, пересекающая эту плоскость и не перпендикулярная ей. Наклонной называют также отрезок, соединяющий точку, не принадлежащую плоскости, с точкой плоскости, и не являющийся перпендикуляром. Соответствие, при котором точке A пространства сопоставляется ортогональная проекция A’, называется ортогональным проектированием на плоскость π. *
Дано: АС ; С АВ — наклонная ВС — проекция a a ВС Доказать: a АВ ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ Если прямая, проведенная на плоскости через основание наклонной перпендикулярна её проекции, то она перпендикулярна и к самой наклонной *
Установить взаимное положение прямых а и в по готовым чертежам Задача1. ABCD – квадрат BE ABCD A b a C B D E Упражнение 3 *
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ Две плоскости называются перпендикулярными, если угол между ними прямой. Теорема. (Признак перпендикулярности двух плоскостей.) Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. *
б) AВB1, CDD1, AB1C1. В кубе A…D1 укажите плоскости, проходящие через вершины куба, перпендикулярные плоскости: а) ABC; б) BCD1. Ответ: а) ABB1, BCC1, CDD1, ADD1, ACC1, BDD1; Упражнение 4 *
ДВУГРАННЫЙ УГОЛ Двугранным углом называется фигура (рис. 1), образованная двумя полуплоскостями, с общей ограничивающей их прямой, и частью пространства, ограниченной этими полуплоскостями. Полуплоскости называются гранями двугранного угла, а их общая граничная прямая – ребром двугранного угла. Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой-нибудь плоскости, перпендикулярной его ребру (рис. 2). Величиной двугранного угла называется величина его линейного угла. *
В кубе A…D1 найдите угол между плоскостями ABC и CDD1. Ответ: 90o. Упражнение 5 *
В кубе A…D1 найдите угол между плоскостями ABC и CDA1. Ответ: 45o. Упражнение 6 *
Точка М равноудалена от всех вершин правильного треугольника ABC, сторона которого равна 4 см. Расстояние от точки М до плоскости ABC равно 2 см. Докажите, что(AMO)(BMC), где O – основание перпендикуляра, опущенного из точки М на плоскость ABC. Найдите угол между (BMC) и (ABC) Найдите угол между прямой MC и плоскостью ABC. Упражнение 9 *
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 968 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 338 человек из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 689 человек из 74 регионов
Ищем педагогов в команду «Инфоурок»
- Таратынова Людмила ИвановнаНаписать 3319 26.11.2018
Номер материала: ДБ-257570
- 22.11.2018 2130
- 20.11.2018 126
- 06.11.2018 1021
- 06.11.2018 388
- 05.11.2018 713
- 01.11.2018 462
- 01.11.2018 394
- 31.10.2018 359
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
Число участников РДШ за 2021 год выросло в три раза
Время чтения: 2 минуты
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📽️ Видео
№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Задание №649 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

№344. Диагонали куба ABCDA1B1C1D1 пересекаются в точке О. Найдите число k такое,Скачать

В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и В1D1. Ответ дайте в градусах.Скачать

№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

№189. Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит этаСкачать

№116. Дан параллелепипед ABCDA1B1C1D1. Докажите, что: а) DC⊥B1C1, и AB⊥A1DСкачать

Как строить сечения параллелепипедаСкачать

№76. Дан параллелепипед ABCDA1B1C1D1. Докажите, что AC||A1C1 и BD||B1D1.Скачать

№194. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащимиСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

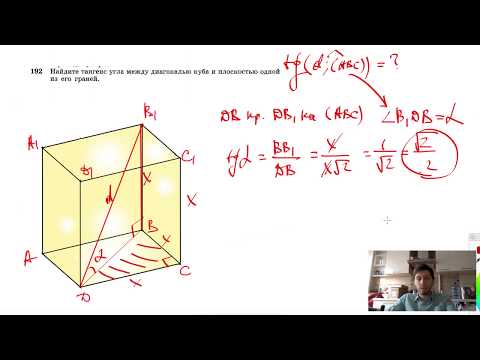
№192. Найдите тангенс угла между диагональю куба и плоскостью одной из его граней.Скачать
Задачи на куб. Диагональ куба - bezbotvyСкачать

№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

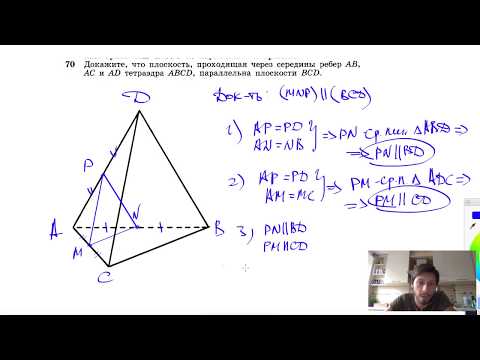
№70. Докажите, что плоскость, проходящая через середины ребер АВ, АС и AD тетраэдра ABCD,Скачать