Как заполнить окружность окружностями (2 видео)

Алгоритм заполнения окружностей

С помощью данного алгоритма можно заполнить (зарисовать) любую окружность.

Теоретическое обоснование метода заключаются в использовании свойства квадрата и теоремы Пито: » в выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны «.

Действительно, любой квадрат является выпуклым четырёхугольником:

Cостоит из четырех точек и четырех последовательно соединяющих их отрезков;
Никакие три из данных точек не лежат на одной прямой;
Соединяющие эти три данных точки отрезки не пересекаются.

Из данного обоснования можно вывести идею,что если любую окружность можно вписать в квадрат, то перебирая все точки, принадлежащие этому квадрату, можно найти все точки,принадлежащие данной окружности или лежащие в ней, если известны координаты центра вписанной окружности и её радиус. Закрасив все такие точки, мы нарисуем и саму окружность, и круг,который этой окружностью ограничен.

Представление алгоритма на языке псевдокода :

1.Получить X и Y координаты окружности, радиус окружности R, цвет заполнения color;
2.Присвоить переменной cX значение левого края (X-R) описанного квадрата ABCD и начать цикл до правого края (X+R)(BD) с шагом в 1 единицу измерения (пиксель)
- 2.1Присвоить переменной cY значение верхнего края (Y+R) и начать цикл от до нижнего края (Y-R)(CD) с таким же шагом
  - 2.1.1.Если значения cX и cY удовлетворяют неравенству (X-cX) 2 +(Y-cY) 2 ≤Radius 2 и в точке с координатами (cX,cY) не стоит точка цвета color, то поставить точку цвета color с координатами (cX, cY)
- 2.2.Закончить цикл по переменной cY
3.Закончить цикл по переменной cX

Данный алгоритм имеет сложность O(N 2 ) и выгодно отличается от обобщенного рекурсивного алгоритма заполнения многоугольников потребляемой памятью, имея примерно такое же время работы применимо к окружности. Также, данный алгоритм гарантированно не переполняет стек вызовов, что позволяет закрашивать ему окружность любого радиуса. Недостатками являются сравнительно малая скорость заполнения и сложность O(N 2 ).

Рис 1. Пример работы алгоритма. Синий квадрат показывает границы квадрата ABCD, внутри которого происходит просчёт принадлежности точек окружности

Содержание

Алгоритм окружности средней точки для заполненных окружностей
5 ответов
обновление
Круги в круге
Задача
Подсказка 1
Подсказка 2
Решение
Послесловие
🎦 Видео

Видео:Дистанционное обучение. Мастер-класс по теме "Изонить. Заполнение угла и круга".Скачать

Алгоритм окружности средней точки для заполненных окружностей

на алгоритм окружности средней точки можно использовать растеризацию границы круга. Однако я хочу, чтобы круг был заполнен, без рисования пикселей несколько раз (это очень важно).

этот ответ обеспечивает модификацию алгоритма, который дает заполненный круг, но некоторые пиксели посещаются несколько раз: быстрый алгоритм для рисования закрашенного круга?

Q: как я могу растеризировать круг без рисования пиксели несколько раз? Обратите внимание, что RAM очень ограничен!

обновление:

нижние пиксели отображаются слишком много раз. Я что-то упускаю?

обновление #2: это решение работает:

Видео:Изонить 03 - Основной алгоритм заполнения окружности / Basic Pattern for Filling a CircleСкачать

5 ответов

ответ на другой вопрос-это прекрасно. Однако, поскольку это создает путаницу, я собираюсь объяснить это немного.

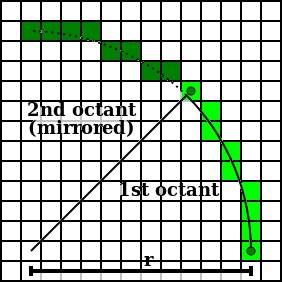
алгоритм, который вы видите в Википедии в основном находит x и y 1/8 окружности (углы от 0 до pi/4 ), а затем рисует 8 точек, которые являются его зеркалами. Например:

то, что предлагает другое решение, которое имеет смысл, если вы внимательно посмотрите на эту картину, — это вместо рисования 8 точек нарисовать 4 горизонтальные линии:

теперь, если вы вычисляете (x,y) для углов в [0, pi/4] и нарисуйте эти 4 линии для каждой вычисленной точки, вы нарисуете много горизонтальных линий, заполняющих круг без какой-либо линии, перекрывающей другую.

обновление

причина, по которой вы получите перекрывающиеся линии в нижней части круга заключается в том, что (x,y) координаты округлены, поэтому в этих местах (x,y) движение горизонтально сами себя.

если вы посмотрите на это Википедия изображение:

вы заметите, что в верхней части круга некоторые пиксели выровнены по горизонтали. Горизонтальные линии, исходящие из этих точек, перекрываются.

если вы не хотите этого, решение довольно легкое. Вы должны сохранить предыдущий x вы нарисовали (так как верхняя и нижняя части являются зеркалами оригинала (x,y) , вы должны сохраняйте предыдущий x, который представляет y этих линий) и рисуйте только горизонтальные линии, если это значение изменяется. Если нет, значит, вы на той же линии.

учитывая тот факт, что вы сначала столкнетесь с самыми внутренними точками, вы должны нарисовать линии для предыдущей точки только новой точки имеет разные x (конечно, последняя строка всегда рисуется). Кроме того, вы можете начать рисовать с угла PI / 4 до 0 вместо 0 до PI / 4 и что вы будете сначала сталкиваются внешние точки, поэтому вы рисуете линии каждый раз, когда вы видите новый x .

Мне нужно было это сделать, вот код, который я придумал для этого. Визуальное изображение здесь показывает пиксели, нарисованные там, где число-это порядок, в котором пиксели пересекаются, а зеленые числа представляют пиксели, нарисованные с использованием отражения завершения столбца с использованием симметрии, как показано в коде.

Я придумал алгоритм, который рисует круг уже заполнен.
Он повторяет пиксели, на которых будет нарисован круг, и ничего больше.
Отсюда все о скорости функции draw-pixel.

что касается алгоритма, вот код:

надеюсь, что это помогает . некоторые новые пользователи . жалко некро-постинг.

Я хотел прокомментировать ваше обновление #2: это решение работает: (но я думаю, что мне нужно больше репутации в первую очередь. ) что в решении есть небольшая ошибка, совпадающая при рисовании небольших кругов. Если вы установите радиус в 1, вы получите

чтобы исправить это все, что вам нужно сделать, это изменить условную проверку в plot4points с

Я проверил это на маленьких и больших кругах, чтобы убедиться, что каждый пиксель по-прежнему назначается только один раз. Кажется, работает отлично. Меня думает х != 0 не требуется. Сохраните немного производительности.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Круги в круге

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Задача

Чему равен наименьший радиус круга, в котором можно разместить без наложений 7 единичных кругов? Обоснуйте ваш ответ.

Примечание. Единичный круг — круг радиуса 1. «Без наложений» означает, что круги могут касаться, но не должны иметь общих внутренних точек.

Видео:Изонить 51 - Новый алгоритм заполнения окружностиСкачать

Подсказка 1

Радиус равен 3, а «оптимальная картинка» выглядит именно так, как вы ее себе, скорее всего, и представили (рис. 1).

Видео:Длина окружности. Математика 6 класс.Скачать

Подсказка 2

Удобно избавиться от понятия «наложение», перейдя от этой задачи к такой:
Рассмотрим вместо кругов только их центры. В круг какого наименьшего радиуса можно их все уместить?

В «оптимальной картинке» все центры являются вершинами и центром правильного шестиугольника со стороной 2 (рис. 2). При этом расстояние между любыми двумя вершинами и центром такого шестиугольника тоже равно 2, поэтому все точки лежат в круге радиуса 2. Нужно обосновать, что все эти точки нельзя уместить в круг меньшего радиуса. Для этого попробуйте рассмотреть случаи, сколько именно (из шести отличных от центра) точек образуют выпуклый многоугольник.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Решение

Будем действовать методом «от противного». Предположим, что шесть точек с попарным расстоянием 2 (или большим двух), удалось поместить в круг радиуса R BA и CH > CA. То есть при сдвиге A в H расстояния до точек B и C увеличились.

Наконец, если все точки лежат на единичной окружности, то они делят ее на 6 дуг, поэтому длина наименьшей из дуг не больше, чем 1/6 длины окружности, то есть не больше 2π/6. Это значит, что величина центрального угла этой дуги также не превышает 2π/6, а значит, расстояние между двумя точками, являющимися концами этой дуги, не больше 2sin(π/6) = 1.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Послесловие

Эта задача является примером огромного класса так называемых «минимаксных» задач вычислительной геометрии. В минимаксных задачах ищется наибольшее возможное значение какой-то величины, которая сама определена как наименьшее значение другой величины. В нашем случае минимаксная задача (к которой мы свели исходную) была такой: сначала среди всех 15 попарных расстояний между шестью точками в единичном круге выбирается наименьшее, а затем ищется такая конфигурация шести точек, для которой это расстояние будет максимальным из возможных.

Приведенное нами утверждение и его доказательство принадлежат замечательному американскому математику Рональду Грэхему (Ronald Graham), они опубликованы в 1968 году. Грэхем доказал даже более общую оценку для наименьшего расстояния d между какими-то из k точек, лежащих в единичном круге. Эта оценка имеет вид

(то есть d не превышает наибольшего из двух чисел — единицы и удвоенного синуса). Оценка Грэхема является оптимальной для 2 ≤ k ≤ 7, то есть существуют картинки, для которых достигаются значения из правой части этого неравенства. Для больших значений k указанная оценка неточна, поскольку она дает d ≤ 1, а на самом деле наибольшее из возможных значений минимального расстояния между точками строго меньше 1.

Естественное обобщение нашей задачи — поиск кругов наименьшего радиуса, в которые можно поместить N единичных кругов (или, что то же самое, поиск решения минимаксной задачи об N точках в единичном круге). В этом поиске усилия математиков сконцентрировались на двух направлениях — компьютерном моделировании и доказательствах оптимальности. Ниже на рис. 5 показаны несколько очевидных оптимальных картинок.

Оптимальность первых трех из них следует из приведенного выше результата Р. Грэхема. Оптимальность последней (для 8 кругов) была доказана в 1963 году голландцем Boele L. J. Braaksma в его диссертации под труднопроизносимым названием «Асимптотические расширения и аналитические продолжения для одного класса интегралов Барнса». Следующее продвижение, а также оптимальность вот такой вот картинки (рис. 6) с двумя внутренними кругами (для 10 кругов)

было получено немцем U. Pirl в 1969 году. Оптимальность аналогичной картинки для 11 кругов доказана еще на 25 лет позже, а для 12, 13 и 19 кругов — еще позже (последний из результатов — в 2003 году).

И. всё. Остальные результаты об упаковке кругов в круг на сегодняшний день находятся в состоянии «оптимальность предполагается, но не доказана». Так что просто полюбуйтесь на картинки (рис. 7) с доказанной оптимальностью (N = 12 и N = 19) и оцените: всего каких-то 15 лет назад это была терра инкогнита, обе задачи еще ждали своего решателя.

А следующие две картинки (для N = 14 и N = 15 соответственно) являются этой самой «инкогнитой» и сейчас (рис. 8). Дерзайте.

См. также:
1) Circle packing in a circle («Упаковка кругов в круг»). Достаточно детальная статья английской Википедии.
2) Circles in Circles. Страничка Эрика Фридмана, откуда мы позаимствовали большую часть иллюстраций. Там же на соседних страницах packing center рассказано о других задачах упаковки.
3) K. A. Dowsland, M. Gilbert, G. Kendall. A local search approach to a circle cutting problem arising in the motor cycle industry (PDF, 346 Кб). Статья в научном журнале Operational Research Society — международного сообщества, занимающегося исследованием операций, то есть научной дисциплиной, чья основная задача — обоснование оптимальности применения каких-либо научных достижений на практике.
В статье объясняется, как можно оптимизировать изготовление «звездочек» и других профилированных колёс (для зубчатых передач и др.) при производстве велосипедов и мотоциклов. С точки зрения математики — абсолютно ничего нового, но связь с практикой очень забавна. Интересно, появится ли когда-нибудь подобная статья для домохозяек — об оптимизации раскладывания котлет на сковородке?