Симметричный треугольник 4 класс

Видео:Ось симметрииСкачать

Осевая и центральная симметрия

О чем эта статья:

Видео:Осевая симметрия, как начертить треугольники симметричноСкачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:4 класс. Математика. Симметричные фигуры. 13.05.2020Скачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Математика. 4 класс. Симметричные фигуры /14.05.2021/Скачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:Математика, 4 класс. СимметрияСкачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

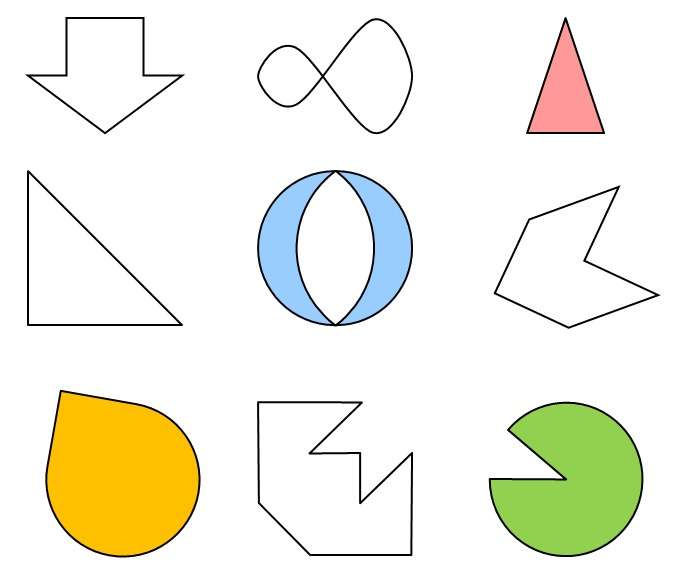
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:Виды треугольников 4 классСкачать

Факультатив по математике в 4-м классе «Симметрия»

Цели:

1. Образовательные:
   • углубить знания о симметрии, сформировать понятие об осевой симметрии;
   • через понятие «симметрия» раскрыть связь математики с живой природой, искусством, техникой.
2. Развивающие:
   • развивать пространственное воображение учащихся, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, обогащать словарный запас учащихся;
   • учить учащихся учиться математике, самостоятельно добывать знания, побуждать к любознательности;
   • развивать мыслительные операции (умение анализировать, сравнивать, обобщать, систематизировать);
   • развивать внимание, наблюдательность.
3. Воспитательные:
   • воспитывать в учащихся дисциплинированность, ответственное отношение к учебному труду, умение к совместной деятельности.

Оборудование:

• Мультимедиа проектор,
• презентация «Симметрия»,
• спички,
• карточки для физ.минутки,
• лист бумаги, краски, кисть (каждому учащемуся),
• буквы, вырезанные из бумаги.

Ход урока

I. Орг. момент.

II. Мозговой штурм.

Как вы знаете, наука геометрия зародилась в глубокой древности. Люди наблюдая за животными, растениями, окружающим миром заметили, что часто половинки разных тел похожи друг на друга, создавая порядок и красоту. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о природе, о форме, размерах и взаимном расположении предметов, он использовал свои геометрические знания, полученные из наблюдений и опытов. Почти все великие учёные древности и средних веков были выдающимися геометрами. Древнегреческий философ Платон, проводивший беседы со своими учениками, одним из девизов своей школы провозгласил: «Не знающие геометрию не допускаются!». Было это примерно 2400 лет назад. Из геометрии вышла наука, которая называется математикой. Мы начнём своё занятие с нескольких практических задач.

Запишите сегодняшнее число и оставьте место для темы урока.

Задача 1. Сложите 7 палочек так, чтобы образовалось 3 треугольника (сторона каждого треугольника должна быть равной длине палочки).

Задача 2. Нарисуйте квадрат. Разделите его на 4 равные части разными способами.

Задача 3. Нарисуйте прямоугольник. Разместите 12 точек в прямоугольнике так, чтобы у каждой стороны в прямоугольнике было по 4 точки.

Задача 4. Графический диктант: Отступите по 3 клеточки сверху и слева и поставьте точку. 1 клеточку вправо, 1-вверх, 1-вправо, 3-вниз, 1-влево, 1-вверх, 1 влево,1-вверх. Отступите 2 клеточки вправо и начертите зеркало. Постройте изображение в зеркале. Кто знает, какую картинку мы получили?

(Все решения проверяются у доски).

III. Новый материал.

С явлением симметрии мы встречаемся повседневно. Удивляемся и восхищаемся, рассматривая крохотную снежинку, стрекозу с прозрачными крыльями или изящный цветок, а может и красивую машину или величественную фигуру самолёта или ракеты. Используя красоту и гармонию природы, человек создал многое в мире симметрии своими руками: купола церквей, архитектурные здания, самолёты, корабли и т.д. Об этих и многих других предметах мы можем сказать, что они красивы. И в основе их красоты лежит симметрия. Но симметрия — это не только красота. Симметричность формы нужна рыбе, чтобы плыть, птице, чтобы летать. Поэтому мы можем сделать вывод, что симметрия в природе неспроста: она ещё и полезна, т.е. целесообразна. В природе красивое всегда целесообразно, а целесообразное всегда красиво. Симметрия проявляется обычно в форме и цвете. Есть симметрия и в музыке, и в поэзии, и даже в буквах и цифрах. Посмотрите, перед вами вырезанные из бумаги некоторые буквы. Симметрия — рождает из них новые буквы. (Демонстрируются буквы А, Г-Т, К-Ж-Л, З, М. Н, Ф-Р и т.д., вырезанные и сложенные по оси симметрии).

IV. Практическая работа.

— А теперь мы с вами используем один из способов построения симметричной картинки. Возьмите лист бумаги и капните (мазните) на него в указанном месте краской. Сложите лист пополам, прогладьте ладошкой и разверните. Что у вас получилось?

— Капля отпечаталась на другой стороне.

— Измерьте расстояния от линии сгиба до каждой картинки. Что вы можете сказать?

— Расстояния по разную сторону от неё одинаковы.

— Может кто-то знает, какая картина получилась с точки зрения математики? (Ответы детей).

— Вы получили симметричную картинку. При этом линия сгиба является осью симметрии. Этот вид симметрии так и называется – осевая симметрия. Подобный приём иногда используют в своём творчестве художники. Если удачно «накапать» краской, то можно получить довольно красивые картинки.

V. Домашнее задание.

Попытайтесь создать свой шедевр в стиле «симметризма» на рисунке «Летом в симметричном лесу». Можете нарисовать от руки или в среде «Живая геометрия» и покажите на рисунке ось симметрии каждого объекта (цветов, деревьев, птиц и т.д.).

VI. Физ.минутка.

Я буду показывать вам геометрические фигуры (Приложение 2), а вы должны догадаться сколько раз выполнять каждое упражнение.

Ай да счёт, игра и только!

VII. Закрепление.

Символом симметрии считается строение и рисунок крыльев бабочки. Сейчас мы с вами посмотрим презентацию «Симметрия». (Приложение 1).

— Итак, какая тема нашего сегодняшнего урока.

— Симметрия.

— Запишите.

— Кто может сказать, что такое симметрия? (Oтветы детей).

Давайте запишем: Симметрия-это соразмерность, одинаковость в расположении частей тела.

— Назовите примеры симметричных тел.

VIII. Физ. минутка.

Дадим зарядку и отдых нашим глазам.

1. Смотрим вправо — вверх; влево — вниз; влево — вверх; вправо — вниз (5 раз)
2. Вверх-вниз; вправо-влево (5 раз)
3. Вращение глазами (можно закрытыми) вправо-влево (по 5 раз)
4. Потёрли ладошки друг о друга и положили на глаза (не надавливая)

IX. Работа со средой «Живая геометрия».

Пройдите к компьютерам, откройте среду «Paint» и выполните задание.

1. Начертите треугольник. Вдоль одной его стороны начертите ось симметрии. Начертите треугольник симметричный первому. Какую фигуру получили?
2. Начертите квадрат. Вдоль одной его стороны начертите ось симметрии. Начертите квадрат симметричный первому. Какую фигуру получили?
3. Начертите квадрат. На некотором расстоянии начертите ось симметрии. Начертите квадрат симметричный первому.
4. Нарисовать геометрического симметричного робота с помощью трёх фигур: квадрата, прямоугольника, треугольника и на рисунке показать все оси симметрии.

X. Тест «Симметрия».

Откройте папку «Симметрия», найдите тест. Приложение 3. Выполните.

IX. Итог урока.

• О чём мы говорили на сегодняшнем уроке?
• Что нового вы узнали?
• Что понравилось?
• Что не понравилось?
• Вы собой довольны? Если да, похвалите себя: похлопайте себе в ладоши или погладьте по головке.

Урок окончен. Всем спасибо!

Используемая литература:

1. Нестеренко Ю.В., Олехник С.Н., Потапов М.К. Лучшие задачи на смекалку.— М.: Научно-технический центр «Университетский»: АСТ-ПРЕСС,1999.
2. Что такое. Кто такой: В 3 т. Т.3—4-е изд., перераб. и доп.—М.: Педагогика-Пресс, 1995.

Видео:Виды треугольников. Построение треугольника | Математика 4 класс #38 | ИнфоурокСкачать

Ось симметрии — что это такое? Фигуры, имеющие ось симметрии

Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, — точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.

Видео:Геометрические фигуры Симметричные и несимметричные фигуры – Математика, 4 класс, урок по обновленнСкачать

Симметрия

Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия — свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.

Вам будет интересно: Как сдать физику и что нужно для этого сделать?

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Вам будет интересно: Гибкость: определение, средства и методы развития гибкости

Видео:Симметричный треугольник фигура технического анализа. Фигура треугольник в трейдингеСкачать

Виды симметрии

Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:

Центральная. Осью симметрии является точка в центре тела, относительно которой при всех преобразованиях части тела равны при наложении.

Видео:Оси симметрии прямоугольника, равнобедренного треугольника, окружностиСкачать

История симметрии

Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.

В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.

А философ Платон считал многогранники олицетворением четырех природных стихий:

• тетраэдр — огонь, так как его вершина направлена вверх;
• куб — земля, так как это самое устойчивое тело;
• октаэдр — воздух, нет каких-либо объяснений;
• икосаэдр — вода, так как тело не имеет грубых геометрических форм, углов и так далее;
• образом всей Вселенной являлся додекаэдр.

Из-за всех этих теорий правильные многогранники называют телами Платона.

Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.

Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».

Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».

Что уж там говорить, симметрия — ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.

Видео:Симметричный треугольникСкачать

Симметрия геометрических фигур и тел

Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.

А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.

Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.

У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.

Видео:Виды треугольниковСкачать

Симметрия в природе

Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия — основное условие.

Видео:Виды треугольниковСкачать

Вывод

Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия — очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием «симметрия» понимают регулярную смену дня и ночи, времен года и так далее.

Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы — астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия — один из основополагающих законов мироздания в целом.

📹 Видео

Дистанционный видеоурок по математике в 4 классе "Симметричные фигуры"Скачать

Ось симметрии. Что это такое и как её проводить?Скачать

Урок 159. Математика. Симметричные фигуры. 4 классСкачать

Осевая симметрия. 6 класс.Скачать

4 класс. Математика. Школа будущего. Симметричные фигуры. 14.05.2020Скачать

4 класс, 25 урок, Площадь прямоугольного треугольникаСкачать

Центральная симметрияСкачать