Чтобы четырехугольник abcd является трапецией по определению нужно чтобы

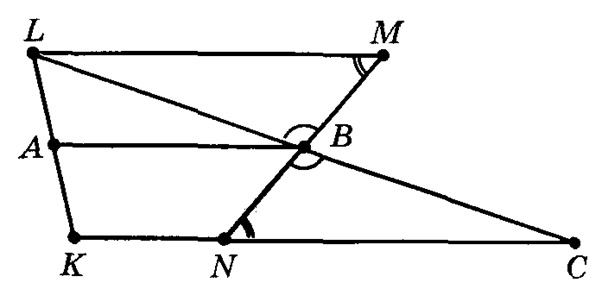
Теорема: Если четырехугольник является трапецией, то ее:

а) средняя линия параллельна основаниям и равна их полусумме;

б) площадь равна произведению средней линии на высоту.

Доказательство.

а) Пусть АВ — средняя линия трапеции KLMN.

Проведем прямую LB, пусть она пересекает прямую KN в точке С. Треугольники LBM и CBN равны, так как у них углы LBM и CBN равны как вертикальные, углы LMB и CNB равны как накрест лежащие при параллельных LM и КС, пересеченных прямой MN, стороны NB и MB равны по условию. Поэтому отрезки LB и ВС равны. Значит, АВ — средняя линия треугольника KLC, а отрезок АВ параллелен отрезку КС и, значит, основанию трапеции KN. А поскольку основания KN и LM параллельны, то средняя линия АВ параллельна и основанию LM. Мы доказали, что средняя линия трапеции параллельна обоим основаниям трапеции. Докажем теперь, что она равна полусумме этих оснований.

В соответствии с теоремой о средней линии треугольника получаем:

Но КС = KN + NC, a NC = LM, поэтому

АВ = 1/2 (KN + NC) = 1/2 (KN + LM) =1/2(KN+LM).

б) Мы знаем, что площадь трапеции равна произведению полусуммы ее оснований на высоту. Но, не забывайте о том, что полусумма оснований равна средней линии. Поэтому площадь трапеции равна произведению средней линии на высоту.

Видео:№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

Задача 30718 Доказать, что четырехугольник ABCD -.

Условие

Доказать, что четырехугольник ABCD — трапеция, если A(3,6), B(5,2), C(-1, -3), D(-5,5).

Решение

По определению трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Так как даны координаты точек, будем искать координаты векторов, задающих стороны трапеции.

Векторы коллинеарны ( лежат на параллельных прямых), если их координаты пропорциональны.

vector и vector коллинеарны.
2:(-4)=(-4):8
vector и vector не коллинеарны.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Тест по геометрии «Свойства и признаки трапеции» (8 класс)

Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Формулировать и доказывать утверждения о свойствах и признаках трапеции, равнобедренной и прямоугольной трапеции. Решать задачи на вычисление, доказательство и построение трапеции, равнобедренной и прямоугольной трапеции.

(Бондарева Наталья Владимировна, учитель математики)

1.Задание : Отметьте правильный ответ:

Многоугольник, называемый трапецией имеет номер :

2.Задание : Отметьте правильный ответ:

Трапецией является четырёхугольник ABCD , по определению нужно, чтобы:

3.Задание : Отметьте правильный ответ:

Несправедливое утверждение для равнобедренной трапеции:

Углы при основании равны

4.Задание : Отметьте правильный ответ:

Утверждение справедливо для любой произвольной трапеции :

Боковые стороны равны

Углы при основании равны

5.Задание : Отметьте правильный ответ:

Сторона HK прямоугольной трапеции HKLM , если LM = 14 см, а L = 150 равна:

6.Задание : Отметьте правильный ответ:

7.Задание : Отметьте правильный ответ:

Углы В и D в трапеции ABCD с основаниями AD и BC при А =50, а С= 100:

8.Задание : Отметьте правильный ответ:

Разность периметров фигур – в прямоугольной трапеции равна :

9.Задание : Отметьте правильный ответ:

Периметр равнобокой трапеции с основаниями 4 см и 10 см, если диагональ является биссектрисой тупого угла трапеции :

1.Задание : Отметьте правильный ответ:

Вид треугольника АВС, при условии , что диагональ острого угла А в трапеции АВС D является биссектрисой данного угла:

2.Задание : Отметьте правильный ответ:

Угол СВЕ в трапеции АВС D , в которой из вершины угла В проведена прямая, параллельная стороне С D и пересекающая сторону А D в точке Е так, что АВЕ = 75, А = 40:

3.Задание : Отметьте правильный ответ:

Углы равнобокой трапеции, в которой разность противолежащих углов

4.Задание : Отметьте правильный ответ:

Периметр равнобедренной трапеции, угол при основании которой равен и основания равны 6см и 10см:

5.Задание : Отметьте правильный ответ:

Углы равнобокой трапеции, в которой противолежащие углы относятся как 2:7

6.Задание : Отметьте правильный ответ:

Периметр трапеции ABCD с основаниями AD и BC , при условии, что AD BC , а на стороне AD отмечена точка К так, что К BCD –параллелограмм и D К = 6см, а периметр треугольника АВК равен 25см :

7.Задание : Отметьте правильный ответ:

Периметр треугольника АВЕ, при условии, что периметр трапеции ABCD с основаниями AD BC равен 32см , а на стороне AD отмечена точка Е так, что Е BCD –параллелограмм и D Е = 5см.

8.Задание : Отметьте правильный ответ:

Длина меньшей боковой стороны прямоугольной трапеции, при условии, что один из углов равен , средняя линия равна 24см, а основания относятся как 3:5

Длина основания AD в трапеции ABCD , при условии, что диагональ В D перпендикулярна к стороне АВ и является биссектрисой угла D , периметр трапеции равен 20 см, а А = 60 , будет равна ______

Правильные варианты ответа: 8; 8см.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Бондарева Наталья ВладимировнаНаписать 2802 04.10.2016

Номер материала: ДБ-237752

04.10.2016 3246

04.10.2016 2746

04.10.2016 1024

04.10.2016 451

04.10.2016 568

04.10.2016 443

04.10.2016 1838

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Россия направит $10,3 млн на развитие школьного питания в нескольких странах

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📸 Видео

8 класс, 4 урок, ПараллелограммСкачать

8 класс, 6 урок, ТрапецияСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

№341. Основанием четырехугольной пирамиды с вершиной Р является трапеция ABCDСкачать

№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать

Трапеция. 8 класс.Скачать

Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

Геометрия. 8 класс. Урок 10 "Площадь четырехугольника"Скачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

11 класс, 44 урок, Описанный четырехугольникСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

8 класс, 15 урок, Площадь трапецииСкачать

Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать

ТрапецияСкачать

Виды трапецийСкачать