Найти главный вектор системы сил если r 2м f1 60н f2 30н f3 30н

2. Плоская система сил.

2.2 Главный вектор и главный момент плоской системы сил.
Приведение к простейшему виду.

2.2.1. Определить главный вектор плоской системы сил, если заданы его проекции на координатные оси R_x = 300Н, R_у = 400Н. (Ответ 500)

2.2.2. Определить главный момент системы двух сил относительно точки А, если силы G = 1Н, F = 5Н, расстояние l = 0,2 м, угол φ = 60°. (Ответ -0,916)

2.2.3. К вершинам квадрата приложены четыре силы F1 = F₂ = F₃ = F4 = 1Н. Определить модуль равнодействующей этой системы сил. (Ответ 2,0)

2.2.4. За центр приведения данной системы сил выбрана точка, расположенная на оси О_у, в которой главный момент равен нулю. Опреде­лить ординату этой точки, если силы
F₁ = F₂ = F₃ = 1Н, F₄ = 2Н, радиус r = 1 м. (Ответ -1,0)

2.2.5. К вершинам равностороннего треугольни­ка приложены силы F₁ = F₂ = F₃ = 1Н.
Опре­делить модуль равнодействующей этой систе­мы сил. (Ответ 1,0)

2.2.6. Заданы силы F₁ = F₂ = F₃ = 12H, F₄ = 14Н. Определить главный момент заданной плоской системы сил относительно точки О, если радиус r = 0,2 м. (Ответ 0,233)

2.2.7. К вершинам прямоугольного треугольни­ка приложены три силы.
Определить значение угла α в градусах, при котором главный мо­мент данной системы си л
М ₀ = -2 кН•м, если сила F₂=4 кН, расстояние l = 1 м. (Ответ 30,0)

2.2.8. К вершинам прямоугольного треугольни­ка приложены силы F₁ = 3Н, F₂ = 6Н, F₃ = 14Н. Определить значение угла а в градусах, при котором главный вектор данной системы сил параллелен оси О_х (Ответ 30,0)

2.2.9. К прямоугольнику приложены четыре силы по 10Н каждая. Определить модуль глав­ного вектора заданной системы сил, если угол α = 60°. (Ответ 22,4)

2.2.10. К квадрату приложены шесть сил по 6Н каждая. Определить главный момент заданной плоской системы сил относительно точки А, если расстояние l = 0,5 м. (Ответ 8,48)

2.2.11. К вершинам квадрата приложены шесть сил по 4Н каждая. Определить главный мо­мент заданной плоской системы сил относи­тельно точки B, если расстояние l = 0,4 м. (Ответ 4,99)

2.2.12. К вершинам прямоугольного треугольни­ка приложены силы F₁ = 12Н, F₂ = 4Н, F₃ = 2Н. Определить значение угла α в градусах, при котором главный вектор данной системы сил параллелен оси О_у. (Ответ 60,0)

2.2.13. К прямоугольнику приложены силы F₁ = 4Н, F₂ = 5Н, F₃ = 8Н, F₄ = 2Н. Определить главный момент заданной системы сил относительно точки А, если расстояние l = 1 м, угол α = 30°. (Ответ 6,89)

2.2.14. К правильному шестиугольнику приложе­ны пять равных по модулю сил. Определить в градусах угол между главным вектором этой системы сил и осью О_х. (Ответ 180)

2.2.15. Задана плоская система сил F₁ = F₂ = F₃ = 2H, F₄ = 10Н. Определить главный мо­мент лой системы сил относительно точки А, если радиус r = 1 м. (Ответ 11,3)

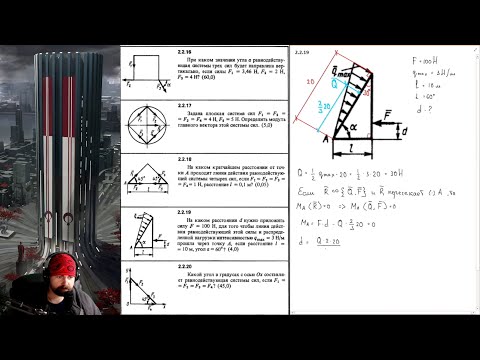
2.2.16. При каком значении угла α равнодейству­ющая системы трех сил будет направлена вертикально, если силы F₁ = 3,46Н, F₂ = 2Н, F₃ = 4Н? (Ответ 60,0)

2.2.17. Задана плоская система сил F₁ = F₂ = F₃= F₄ = 4Н, F₅ = 5Н. Определить модуль главного вектора этой системы сил. (Ответ 5,0)

2.2.18. На каком кратчайшем расстоянии oт точ­ки А проходит линия действия равнодействую­щей системы четырех сил, если F₁ = F₂ =F₃ = F₄ = 1H, расстояние l = 0,1 м? (Ответ 0.05)

2.2.19. На каком расстоянии d нужно приложить силу F = 100Н, для того чтобы линия
дейст­вия равнодействующей этой силы и распреде­ленной нагрузки интенсивностью
q_max = 3 Н/м прошла через точку А, если расстояние l = 10м, угол α = 60°? (Ответ 4,0)

2.2.20. Какой угол в градусах с осью О_х составляет равнодействующая системы сил,
если F₁ = F₂ = F₃ = F₄? (Ответ 45,0)

2.2.21. К квадрату приложена система четырех сил, причем силы F₁ = F₂ = F₃ = 1Н.
Опреде­лить модуль силы F₄, при которой равнодейст­вующая системы R = 2Н. (Ответ 1,0)

Видео:определение реакций в стержнях от действия грузовСкачать

Задание на расчетно-графическую работу №2. Фрагмент методички с заданиями, которые задают где-то на Дальнем Востоке. Задания не являются оригинальными и взяты из другой методички. Образцы оформления здесь

Задача 1. Пример
Для балок построить эпюры поперечных сил и изгибающих моментов. Данные для задачи своего варианта взять из таблицы 5

Задача 2. Пример
Определить аналитическим способ усиления в стержнях АВ и ВС заданной стержневой системы (рис. 2). Исходные данные для задачи своего варианта взять из таблицы 2

Задача 3. Пример
Определить реакции опор балки нагруженной как показано на схеме (рис. 5). Исходные данные приведены в таблице 3

Задача 3. Схемы. Пример
Определить реакции опор балки нагруженной как показано на схеме (рис. 5). Исходные данные приведены в таблице 3

Задача 4. Пример
Определить положение центра тяжести сложной фигуры, ее сечение имеет вид (см. рис. 8). Данные для задачи своего варианта взять из таблицы 4

Задание №18. Пример

1. Определить положение расчетного центра тяжести фигуры, размеры указаны в мм.
2. Вырезать фигуру из плотной бумаги.
3. Методом подвешивания определить опытное положение центра тяжести.
4. Сравнить полученные результаты

4.4. Пример
Чему равно наибольшее касательное напряжение в толстой части ступенчатого вала, если в тонкой части оно 135 МПа?
Ответ: τ_max2=80 МПа

10. Поезд весом 3000 кН идет со скоростью 36 км/ч. Сила сопротивления движению составляет 0,005 веса поезда. Определить полезную мощность тепловоза. Движение прямолинейное по горизонтальному пути

Вариант 5 Пример
Определить проекцию равнодействующей системы сил на ось 0у F₁=10 кН F₂=8 кН F =20 кН
Как направлен вектор равнодействующей силы, если известны величины его проекции? 11Н 23,59 Н Определить αx
Какой вектор силового многоугольника является равнодействующей силой?
Груз F находится в равновесии. Указать, какой из силовых треугольников для шарнира В построен верно.
Груз F находится в равновесии. Указать, какие условия для точки равновесия В записаны верно

5.4.7 Пример
В центре приведения О главный вектор R=5 Н и главный момент МO=25 Нм. Определить значение главного момента в центре приведенияя А, если ОА=1 м

5.4.8 Пример
При приведении системы сил к центру О получены главный вектор R=10 Н и главный момент М0=20 Нм. Определить модуль главного момента в центре приведения А, если расстояние ОА=2 м

ЗАДАЧА №12. Пример
Стержень AB длиной 60 см скользит своими концами и по сторонам угла. Определить скорости точек В и С, а также угловую скорость стержня, если скорость точки А равна 10 см/с

ЗАДАЧА 8. Пример
Для изображенной на схеме передачи определить вращающий момент Т₂ на ведомом валу. Исходные данные: мощность на ведущем валу Р₁=8 кВт; угловая скорость ведущего вала ω₁=40 рад/с; коэффициент полезного действия передачи η=0,97; передаточное число передачи u=4

Промежуточная контрольная работа по Технической механике. Вариант 10. Пример
• Задание №1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях.
• Задание №2. Груз подвешен на стержнях и канатах находится в равновесии. Определить усилия в стержнях.
• Задание №3. Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом

ВАРИАНТ 6. Задача 1 Пример
Определить реакции стержней кронштейна АВС, изображенного на схеме (рис.5), если сила F направлена вертикально вниз.
Стержни АВ и ВС считать жесткими, невесомыми. Точки А, В, С — цилиндрические шарниры.
Значение силы F, углы α, β сведены в таблице

2. Пример
В соединениях 1 и 2 кронштейн закреплен на колонне болтами, установленными в отверстиях с зазором. Какой из вариантов, при прочих равных условиях, рациональнее, если в качестве критерия рациональности принять нагрузочную способность

Задание 3.
К тормозному колесу диаметром 370 мм, жестко посаженному на вал двигателя, прижимают с помощью рычага тормозную колодку силой F=180 Н.
Вал вращается при этом равномерно и делает 1950 об/мин.
Коэффициент трения между колесом и колодкой 035. Опрсдедкть мощность (в кВт и л.с.) развиваемую двигателем, если потери на трение и нем составляют 15%

Колесный трактор имеет двигатель, развивающий максимальную Мощность 62.5 кВт КПД трансмиссии трактора 0.72 масса трактора вместе с перевозимым грузом 2250 кг.
Определить наибольшую скорость движения в км/ч, с которой может двигаться трактор по асфальтированной дороге, коэффициент трения равен 0.18

КОНТРОЛЬНАЯ РАБОТА № 1. Вариант 3

Задача 1. Пример Определить реакции стержней, удерживающих грузы F₁ и F₂ . Массой стержней пренебречь. F₁=0,6 кН F₂=0,4 кН
Задача 2. Пример Определить реакции опор двухопорной балки. q=10 Н/м F=16 Н М=14 Нм
Задача 3. Пример Определить центр тяжести плоской фигуры
Задача 4. Пример Скорость самолёта при отрыве от взлётной полосы должна быть 300 км/ч. Определить минимальную длину взлётной полосы, необходимую для того, чтобы лётчик при разгоне испытывал перегрузку, не превышающую его утроенный вес.
Задача 5. Пример Определить реакции опор балки. F=18 Н q=2 Н/м

Вариант 1 Пример
1. Определить проекции силы F=14 Н на оси координат.
2. Определить моменты сил относительно указанной точки. Дано: F₁=25 Н, F₂=14 Н, F₃=28 Н, а=20 см, b=50 см.
3. Чему равено модуль силы Р, если её проекции Px=9 Н, Py=-12 Н.
4. Найти моменты сил относительно осей

Тест l-го уровня. Сдвиг, срез, смятие Пример
Во всех заданиях выбрать номер правильною ответа
Задание 1. Если в поперечных сечениях элемента возникает, внутренний силовой фактор — поперечная сила, то такой вид деформации называется: растяжением сдвигом смятием
Задание 2. Поперечная сила действует: в плоскости поперечного сечения бруса перпендикулярно плоскости поперечного сечения бруса вдоль продольной оси бруса
Задание 3. Единица измерения напряжения 1 Па составляет: Н/мм 2 кг/см 2 Н/м 2 (модуль сдвига)

Тест l-го уровня. Сдвиг, срез, смятие Пример
Задание 4. Болт нагружен растягивающей силой F. Рассчитать величину площади смятия, если d=20 мм, h=14 мм, D=36 мм 468 224 1331 703 мм 2
Задание 5. Из условия прочности болта на смятие определить величину допускаемой нагрузки F, если [τ_ср.]=100 МПа, [σ_см]=240 МПа, используя данные задания 4 22,4 кН 84.3 кН 168,7 кН 70,3 кН
Задание 6. Установить соответствие в формуле зависимости между тремя упругими постоянными материала: G = E/2(1-μ) Коэффициент Пуассона Модулем упругости 1-го рода Модулем упругости 2-го рода (модуль сдвига)

Тест. Эпюры балок. Очертания контуров эпюр Пример
Указать соответствие между схемой балки и эпюрами Q и М. Схема ответа

Тест. Эпюры простых балок
Установить соответствие между схемой балки и эпюрами поперечных сил Q и изгибающих моментов М. Схема ответа Q — а) М — б)

Гарантии (в плюсиках тоже есть текст)

Посмотрите на мой сайт. Все виды связи, почта и группа , в ней отзывы реальных людей, вы можете им написать, и, если человек ответит, пообщаться с ним. Может быть знакомого найдете.
Клиент, довольный работой, возвращается еще, приводит друга, заказывает для товарища. Причем чем быстрее он получит качественную работу, тем выше вероятность повторного заказа. Это правило проверено многолетней практикой. Не сомневайтесь. Мой бизнес строится на репутации.

Видео:2.2. Главный вектор и главный момент плоской системы сил. Приведение к простейшему видуСкачать

Теоретическая механика (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6

В связи с решением подобных задач методом проекций необхо­димо отметить следующее. Применяя метод проекций к определению равнодействующей любого числа сходящихся сил, наиболее удобно использовать обычную прямоугольную систему координат­ных осей. При этом найденные проекции равнодействующей и иско­мая равнодействующая образуют прямоугольный треугольник, решая который легко определить модуль и направление равнодействующей. Применяя метод проекций к решению задач на равновесие сил, совсем не обязательно использовать взаимно перпендикулярные оси.

В тех случаях, когда оп­ределяются модули сил, на­правления которых заданы, каждую из осей целесообраз­но расположить перпендику­лярно к направлению иско­мых сил. Тогда в каждое урав­нение равновесия войдет только одно неизвестное.

Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

§ 5. Условия равновесия плоской системы сходящихся сил

Если система сходящихся сил находится в равновесии, то ее равнодействующая R = 0, следовательно,

Очевидно, что данное выражение будет обращаться в нуль, если

(5)

Можно применить упрощенную запись Уравнения (5) выражают условия равновесия плоской системы сходящихся сил в аналитической форме.

Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций этих сил на каждую из двух координатных осей равнялись нулю.

Метод проекций при решении задач на равновесие системы особенно удобен в том случае, если в систему входит более трех сил.

Задача 12. На оси шарнира В (рис. 23) шарнирно-стержневой системы ABC свободно вращается блок. Через блок перекинута нить, с помощью которой удер­живается груз весом G = 50 Н. Определить усилия в стержнях АВ и ВС. При этом диаметром блока и трением нити можно пренебречь.

1. Выделить точку, равновесие которой следует рассмотреть. В данной задаче это будет точка В неподвижного блока.

2. Изобразить векторы всех активных сил, действующих на нее. В нашем примере это натяжение вертикальной ветви нити, равное весу груза, и натяжение горизонтальной ветви нити.

3. Мысленно отбросить связи и заменить их реакциями R1 и R2.

4. Все силы изобразить в виде векторов (рис. 23).

Предположив, что стержни АВ и ВС растянуты, направить соответственно реакции R1 и R2 от узла В.

5. Выбрать направление координатных осей х и у.

6. Составить два уравнения равновесия:

Учитывая, что F = G = 50 H, и решая совместно оба уравнения, получим R1 = – 18,6 H; R2 = – 68,5 Н. Здесь знаки «минус» указывают, что стержни АВ и ВС сжаты, а не растянуты, как мы предполагали заранее.

Видео:Система сходящихся силСкачать

Глава 2. ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ

Видео:Вечный предохранитель!!! Секрет автоэлектрика. Как найти короткое замыкание при помощи лампочкиСкачать

§ 6. Момент силы относительно точки

Если к телу, закрепленному при помощи шарнира (рис. 24), приложить силу F, то эта сила будет стремиться вращать тело относительно центра шарнира О (вокруг оси, перпендикулярной к плоскости чертежа).

Вращающее действие силы измеряют величиной, называемой моментом силы. Момент силы относительно точки равен произведению модуля силы на кратчайшее расстояние от данной точки до линии действия силы.

Величину момента обозначают буквой М, а расстояние ОМ от точки до линии действия силы, которое называют плечом силы, – буквой а. Точку О называют центром момента. Чтобы найти плечо силы, нужно опустить перпендикуляр из центра момента на линию действия силы F. Момент силы принято считать положительным, если сила стремится вращать тело вокруг центра моментов (в плоскости чертежа) по часовой стрелке, и отрицательным – в противном случае. Таким образом, в общем виде

(6)

Так как сила измеряется в ньютонах, а расстояние в метрах, то момент имеет размерность: Н×м.

Момент силы относительно точки можно рассматривать как удвоенную площадь треугольника АОВ (см. рис. 24):

где АВ – основание треугольника, а ОМ – его высота.

Из определения момента силы относительно точки очевидно следующее:

модуль и знак момента не изменяются при переносе силы по линии ее действия либо центра моментов по прямой, параллельной линии действия силы;

момент силы относительно точки равен нулю, если центр мо­ментов лежит на линии действия силы.

Задача 13. Определить моменты сил F1, F2, F3, F4 относительно точки А (рис. 25), если АВ = 0,7 м; AD = 0,4 м; АС = 0,2 м; F1 = 10 Н; F2 = 25 Н; F3 = 5 Н; F4 = 8 Н.

1. Момент силы F1 относительно точки А положительный, а плечо силы равно АВ, поэтому

2. Момент силы F2 относительно точки А отрицательный, так как сила F2 стремится вращать тело АВ против часовой стрелки. Из треугольника ADE плечо силы F2 АЕ = AD cos 45°, следовательно,

3. Момент силы F3 относительно точки А положительный. Из треугольника АКС плечо силы F3 AK = ACcos 45°, следовательно,

Линия действия силы F4 пересекает центр моментов, значит

Задача 14. Определить моменты шести заданных сил (рис. 26) относительно точек А, В и С, если P1 = 30 Н, Р2 = 50 Н, Р3 = 25 Н, Р4 = = 40 Н, Р5 = 35 Н, Р6 = 54 Н, АВ = 1,2 м, ВС = 0,8 м, a = 55° и b = 35°.

Решение 1 – определение моментов шести заданных сил относительно точки А (рис. 26, а).

1. Центр моментов в точке А. Через точку А проходят линии действия трех сил , и Значит для этих сил плечи равны нулю. Следовательно,

2. Находим момент силы . Опу­стив из точки А на линию действия силы перпендикуляр AD, получим плечо силы Длину AD легко най­ти, так как это катет треугольника ABD:

3. Величина момента отрицательная (сила поворачивает плечо AD вок­руг точки А по ходу часовой стрелки), следовательно,

4. Находим момент силы Плечом силы является перпендикуляр АЕ к СЕ – линии действия силы Из тре­угольника АСЕ

Величина момента положительная (плечо АЕ поворачивается около точки А силой против хода часовой стрел­ки). Следовательно,

5. Находим момент силы Плечом силы относительно точ­ки А является отрезок АС, так как сила направлена к АС перпендикулярно. Величина момента отрицательная:

Решение 2 – определение моментов сил относительно точки В (рис. 26, б).

1. Центр моментов в точке В.

2. Через точку В проходят линии действия двух сил: и . Следовательно,

и

3. Находим момент силы Плечо силы :

Величина момента отрицательная:

4. Находим момент силы Плечо силы :

5. Находим момент силы Плечо силы :

Величина момента положительная:

6. Находим момент силы Плечом силы является отре­зок ВС. Момент положительный:

Решение 3 – определение моментов сил относительно точки С (рис. 26, в) рекомендуется выполнить самостоятельно.

В некоторых задачах силы расположены так, что либо их плечи определяются очень просто – как катеты прямоугольных треугольников, в которых даны гипотенузы, либо плечи заданы в условии задачи (ВС и АС).

Но иногда некоторые силы заданной системы оказываются расположенными относительно выбранного центра моментов так, что определить длину плеча трудно и требуется, например, предвари­тельно вычислить длины еще одного-двух отрезков. В таких слу­чаях целесообразно силу разложить на две составляющие и при­менить для определения ее момента теорему Вариньона.

Задача 15. Определить моменты относительно точки А сил P1 = 40 H; P2 = 60 H; Р3 = 030 H и Р4 = 50 H, приложенных в точках A, В и С, как показано на рис. 27, а. Углы a = 30°, b = 50°, АB = 2,5 м; ВС = 1,5 м.

1. Относительно точки А моменты сил , и определяются по выражениям (рис. 27, а):

2. Находим момент силы

Вариант 1-й (рис. 27, а). Плечо АЕ силы в данном слу­чае определяем из D AEF, в котором известен только Ð EAF = b. Значит, нужно предварительно определить одну из сторон. Найдем AF:

Величину FB находим из D CBF, в котором Ð BCF =b:

И теперь можем определить плечо АЕ:

Раскрываем скобки и заменяем :

Момент положительный, следовательно:

Вариант 2-й. Чтобы избежать определения плеча АЕ, кото­рое в данном случае находится после предварительного вычисления двух отрезков (FB и AF), необходимо момент силы относительно точки А найти по теореме Вариньона: момент равнодействующей плоской системы сил относительно любой точки, лежащей в той же плоскости, равен алгебраической сумме моментов составляющих сил относительно той же точки.

Разложим силу на две составляющие: одну, направленную вдоль отрезка ВС, и другую – перпендикулярно к нему (рис. 29, б).

Модуль первой составляющей P4 cosb, а ее плечо – отрезок АВ, длина которого задана. Модуль второй составляющей P4 sinb, а ее плечо АК = ВС = 1,5 м.

Применяя теорему Вариньона, получаем

Как видно, получено точно такое же значение момента, что и в первом варианте решения:

Видео:Видеоурок 1. Определение реакций жёстких стержней.Скачать

§ 7. Приведение системы сил
к данной точке

Если линии действия сил, приложенных к телу, расположены как угодно на плоскости, то их неудобно складывать непосред­ственно. Целесообразно сначала упростить систему, т. е. заменить ее более простой эквивалентной системой. Такая замена называется приведением системы к данной точке. Эту точку принято называть центром приведения.

Предварительно докажем теорему о параллельном переносе силы: Силу, приложенную к твердому телу в данной точке, можно перенести параллельно в любую другую точку тела, присоединяя при этом пару. Момент присоединенной пары равен моменту данной силы относительно точки, в которую эту силу перенесли (привели).

Доказательство: Пусть сила F приложена к телу в точке А (рис. 28). Приложим в центре О две равные и противоположно направленные силы: F’ и F». Согласно 2-й аксиоме при этом механическое состояние тела не изменится. Пусть модули всех сил равны: F = F’ = F». Тогда полученную систему из трех сил можно представить как пару (F, F») и силу F’, которую можно рассматривать как перенесенную из точки А в точку О силу F. Нетрудно убедиться, что момент пары (F, F»)

В частном случае, если центр приведения выбрать на линии действия силы F, то момент присоединенной пары будет равен нулю. Значит, присоединять пару необходимо только при парал­лельном переносе силы.

Рассмотрим теперь произвольную плоскую систему из n числа сил (F1, F2, F3, . Fn) (рис. 28). Выберем на плоскости произ­вольную точку О и перенесем в нее все силы системы. В результате приведения получим пучок приложенных в точке О сил (F’1, F‘2, F‘3, . F’n) и систему присоединенных пар Моменты этих пар соответственно равны:

(7)

Сложим все силы пучка при помощи построения силового многоугольника (рис. 29) и получим их равнодействующую R0:

Затем сложим все присоединенные пары и получим одну равнодействующую пару с моментом М = М1 + М2 + М3 + . + Мп. Итак, произвольная система сил эквивалентна одной силе и одной паре, которые носят название главный вектор и главный момент системы.

Можно сказать, что главный вектор – это вектор, предста­вляющий собой геометрическую сумму всех заданных сил, перенесенных параллельно самим себе в точку О, называемую цен­тром приведения.

Модуль главного вектора можно определить по его проек­циям Rx и Ry на оси координат Ох и Оу (см. рис. 29) по формуле где на основании теоремы о проекции равно­действующей на ось:

(8)

Направление главного вектора определяется из выражений и , где a – угол между главным вектором и положительным направлением оси х.

Модуль главного момента системы получим, используя урав­нения (7):

(9)

Откуда модуль главного момента системы равен алгебраиче­ской сумме моментов всех сил системы относительно центра при­ведения.

Если за центр приведения принять другую точку, то нетрудно убедиться, что модуль и направление главного вектора будет та­ким же, т. е. они не зависят от выбора центра приведения.

Что же касается главного момента системы, то его модуль и направление зависят от выбора центра приведения, так как при изменении положения центра приведения изменяются плечи сил заданной системы, а следовательно, и их моменты. Следует также отметить, что главный вектор не является равнодействующей системы, хотя по модулю и направлению совпадает с ней. Рас­смотренный случай приведения системы, когда R0 ¹0 и М¹0, является общим.

Возможны следующие частные случаи приведения:

а) главный вектор оказался равным нулю, а главный момент не равен нулю (R0 = 0, М ¹ 0), т. е. система эквивалентна одной только паре;

б) главный вектор не равен нулю, а главный момент равен нулю (R0 ¹ 0, М = 0), т. е. система сводится к одной силе, и очевидно, что главный вектор есть равнодействующий этой системы;

в) главный вектор и главный момент системы равны нулю (R0 = 0, М = 0) – система находится в равновесии.

Видео:5.3. Главный момент произвольной пространственной системы силСкачать

§ 8. Равнодействующая плоской системы сил.
Теорема Вариньона о моменте равнодействующей

Рассмотрим более подробно общий случай приведения системы, когда R0 ¹ 0 и М ¹ 0. Можно убедиться, что в этом случае система имеет равнодействующую, приложенную в некоторой точке, не совпадающей с центром приведения.

Пусть данная система сил приведена к главному вектору R0, приложенному в точке О (рис. 30), и главному моменту системы М (пара RR’). Представим последний в виде пары сил, у которых модуль равен модулю главного вектора системы. Одну из сил пары R’ приложим в центре приведения О и направим противо­положно главному вектору системы. Тогда точку приложения второй силы пары R найдем, если вычислим плечо пары:

Силы R0 и R’, равные и противоположно направленные, вза­имно уравновешиваются, их можно отбросить согласно 2-й аксиоме статики. Остается одна сила R = R0, заменившая собой заданную систему сил. Она и является равнодействующей этой системы. Таким образом, мы доказали, что в общем случае, когда главный вектор и главный момент системы не равны нулю, система имеет равнодействующую, равную по модулю и направленную парал­лельно главному вектору в ту же сторону.

Модуль момента равнодействующей R относительно центра приведения О:

но произведение Ra выражает модуль главного момента системы, следовательно, учитывая выражение (9), имеем

. (10)

Следовательно, момент равнодействующей произвольной плоской системы сил относительно любого центра равен алгебра­ической сумме моментов всех сил системы относительно этого же центра (теорема Вариньона).

Плоскую систему сходящихся сил и плоскую систему парал­лельных сил следует рассматривать как частные случаи произ­вольной системы. Для них также справедлива теорема Вариньона.

Теоремой Вариньона широко пользуются при решении различ­ных задач статики. В частности, ее применяют при определении равнодействующей системы параллельных сил.

Пусть задана плоская система параллельных сил (рис. 31). Найдем главный вектор этой системы по его проекциям на оси координат, направив ось Оу параллельно, а ось Ох – перпенди­кулярно данным силам. При этом будем учитывать, что главный вектор равен по модулю равнодействующей системы, параллелен ей и направлен в ту же сторону:

Так как то вектор равнодействующей напра­влен параллельно составляющим силам, а модуль ее

т. е. модуль равнодействующей системы параллельных сил равен алгебраической сумме проекций сил системы на ось, параллельную этим силам. Знак алгебраической суммы показывает, в какую сторону направлена равнодействующая: «плюс» – равнодействующая направлена в сторону положительного направления оси проекции, «минус» – в противоположном направлении. Выбрав центр моментов в произвольной точке О, по теореме Вариньона найдем расстояние ОА, определяющее положение линии действия равнодействующей R.

Задача 16. К телу в точках А и В приложены параллельные силы F1 = 20 Н, F2 =60 H и F3 = 18 Н (рис. 32). Определить модуль, направление и линию действия равнодействующей.

1. Приняв точку А за начало координат, направим ось х перпендикулярно данным силам, а ось у параллельно им.

2. Найдем модуль равнодействующей:

Так как знак алгебраической суммы проекций получился отрицательным, то вектор равнодействующей направлен вниз, в сторону отрицательного направле­ния оси Y.

3. Приняв точку A за центр моментов, на основании теоремы Вариньона запишем:

Учитывая, что найдем расстояние АС между линиями действия и равнодействующей из выражения

Задача 17. Определить равнодействующую двух параллельных сил и , направленных в одну сторону (рис. 33, а) если P1 = 12 H и P2 = 15 H.

1. Примем за начало осей проекций точку А. Ось x расположим перпендикулярно к данным силам и направим ее вправо, а ось у направим вдоль силы вниз (рис. 33, б).

2. Найдем модуль равнодействующей:

Следовательно, R = 27 H.

Так как сумма проекций положительна, то вектор равнодействующей направлен тоже вниз.

3. Приняв за центр моментов точку А, найдем расстояние АС от точки А до линии действия равнодействующей.

В данном случае ,

Таким образом, равнодействующая двух данных сил численно равна 27 Н, и линия ее действия расположена от точки А на расстоянии АС = 1 м (рис. 33, в).

Задача 18. Какова должна быть масса однородной доски (рис. 34, а), чтобы, опираясь в точке В на гладкую опору, она с положенными на нее грузами т1 = 100 кг и m2 = 48 кг находилась в равновесии? Центр тяжести доски расположен в точке С.

1. Рассматривая доску как рычаг, видим, что на нее действуют три нагрузки: вес левого груза G1 = mlg, вес правого груза G2 = m2g и собственный вес доски Gд = mдg (рис. 34, б).

2. Для равновесия доски необходимо, чтобы алгебраическая сумма моментов этих сил относительно опоры В равнялась нулю. Следо­вательно,

3. Подставив вместо весов их выражения через массы и разде­лив обе части равенства на постоянную величину g (ускорение сво­бодного падения 9,81 м/сек2), получим

4. Отсюда находим массу доски:

Видео:1 Решение задачи графическим и аналитическим методомСкачать

§ 9. Уравнения равновесия произвольной плоской системы сил

Произвольная плоская система сил будет в равновесии, если главный вектор и главный момент системы будут равны нулю, т. е. R = 0 и М = 0. Эти условия являются необходимыми и достаточными. Действительно, равенство R = 0 означает, что геометрическая сумма сил системы, перенесенных в произвольно выбранный центр приведения, равна нулю, т. е. эти силы уравно­вешены. Из равенства М = 0 следует, что сумма моментов при­соединенных пар равна нулю, а это есть необходимое и достаточное условие равновесия системы пар.

Выше было показано, что модуль главного вектора системы можно определить по его проекциям на оси координат:

а модуль главного момента системы:

Поэтому выражение условия равновесия системы можно за­писать в следующей форме:

Откуда следует, что для равновесия плоской системы произ­вольно расположенных сил необходимы и достаточны три условия:

(11)

Сокращенная запись условий:

(12)

т. е. алгебраическая сумма проекций всех сил системы на ось х равна нулю; алгебраическая сумма проекций всех сил системы на ось у равна нулю; алгебраическая сумма моментов всех сил системы относительно любой точки равна нулю.

Первые два уравнения равновесия называют урав­нениями проекций, третье – уравнением мо­ментов.

Наряду с этой основной формой уравнений плоской системы сил можно доказать справедливость еще двух форм.

Первая форма уравнений:

(13)

т. е. для равновесия произвольной плоской системы необходимо и достаточно, чтобы равнялись нулю алгебраические суммы момен­тов всех сил относительно двух точек плоскости и алгебраическая сумма проекций всех сил на одну ось, но не перпендикулярную к прямой, соединяющей центры моментов А и В.

Вторая форма уравнений:

(14)

т. е. для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов относи­тельно трех точек плоскости, но не лежащих на одной прямой, равнялись нулю.

Нетрудно убедиться, что плоская система сходящихся сил и плоская система пар являются частными случаями произвольной плоской системы сил. Действительно, если за центр приведения выбрать точку пересечения линий действия всех сил, главный момент системы относительно этой точки равен нулю и система сводится к одному главному вектору. Для равновесия необходимо удовлетворение только двух условий: Плоская система пар, как известно, сводится только к результирующей паре, а главного вектора не существует. Следовательно, для равновесия системы пар необходимо и достаточно только одно условие:

Существует еще третий частный случай – это система парал­лельных сил.

Пусть к телу будет приложена система сил F1, F2, F3, …, Fn, линии действия которых параллельны друг другу (рис. 35). Так как ось х перпендикулярна всем силам, то условие будет всегда выполняться, даже если система не уравновешена. Следовательно, условия равновесия плоской системы параллель­ных сил выражаются уравнениями

где А и В – произвольно выбранные точки на плоскости.

Задачи на равновесие произвольной плоской системы сил должны содержать не более трех неизвестных, а на равновесие плоской системы параллельных сил – не более двух неизвестных. Если неизвестных больше, чем уравнений статики, то задача ста­новится статически неопределимой, для ее решения потребуются дополнительные уравнения, которые будут рассмотрены в раз­деле 2.

Для решения задачи составляют уравнения равновесия одним из трех указанных способов. Для проверки правильности решения задачи можно составить четвертое уравнение равновесия из числа неиспользованных в ходе решения задачи.

Задача 19. Однородный брус АВ (рис. 36) весом G = 250 Н прикреплен к стене при помощи шарнира А и в точке D опирается на гладкий цилиндр. В точке Е к брусу подвешен груз Р = 800 Н. Определить реакцию цилиндра и шарнира, если АЕ = 1,2 м; АС = ВС = 1,5 м; AD = 1,7 м и Ð ВАх = a = 40°.

1. Рассмотрим равновесие бруса АВ.

2. Приложим к брусу активные силы: собственный вес G в центре тяжести С (для однородного бруса центр тяжести расположен посередине) вертикально вниз и силу F – от веса груза.

3. Связями для бруса являются цилиндр и шарнир. Мысленно освобождаемся от связей и заменяем их реакциями. Реакция гладкого цилиндра RD направлена по нормали к поверхности цилиндра в точке касания D. Реакция шарнира RA приложена в центре шарнира А. Так как направление реакции неизвестно, заменим ее двумя составляющими Rx и Ry, направив их по осям Ох и Оу. Направ­ление осей показано на рис. 36. Центр моментов выбираем в точке А.

4. Составим три уравнения равновесия, так как активные силы и реакции связей составляют произвольную плоскую систему сил:

Из третьего уравнения находим RD:

Из первого уравнения

Из второго уравнения

Для проверки правильности решения составим уравнение моментов относи­тельно точки С:

Подставим в уравнение найденные значения сил Rx, Ry и RD:

Уравнение превратилось в тождество, следовательно, задача решена верно.

Задача 20. На горизонтальную балку АВ, левый конец кото­рой имеет шарнирно-неподвижную опору, а правый – шарнирно-подвижную, в точках С и D поставлены два груза: P1=10 кН и P2 = 20 кH (рис. 37, а). Определить реакции опор балки.

📽️ Видео

Урок 38 (осн). Сложение сил, направленных по одной прямой. РавнодействующаяСкачать

КОРОТКОЕ ЗАМЫКАНИЕ КАК УСТРАНИТЬСкачать

Приведение системы сил к простейшему видуСкачать

27. Статически неопределимый стержень ( растяжение-сжатие ) ( практический курс по сопромату )Скачать

Система сходящихся сил. Решение задач по МещерскомуСкачать

Практика_№7_Равновесие_пространственной_системы_сил_2_часаСкачать

Определение реакций опор простой рамыСкачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Зачем нужен ассемблер на примере. Соглашения о вызовах в разных архитектурахСкачать

§4.3. Главный вектор и главный момент сил инерцииСкачать

Приведение системы сил к простейшему видуСкачать

Момент силы относительно точки и осиСкачать