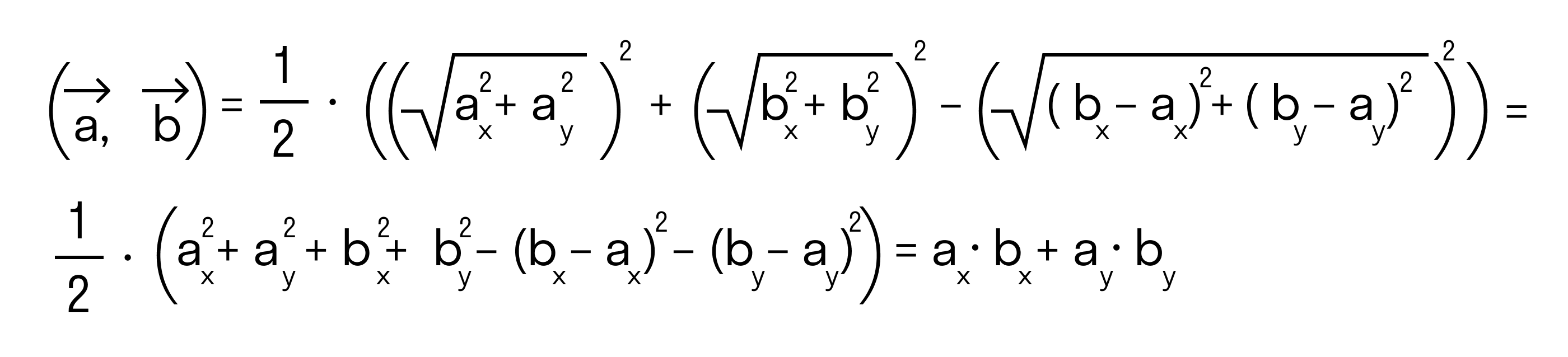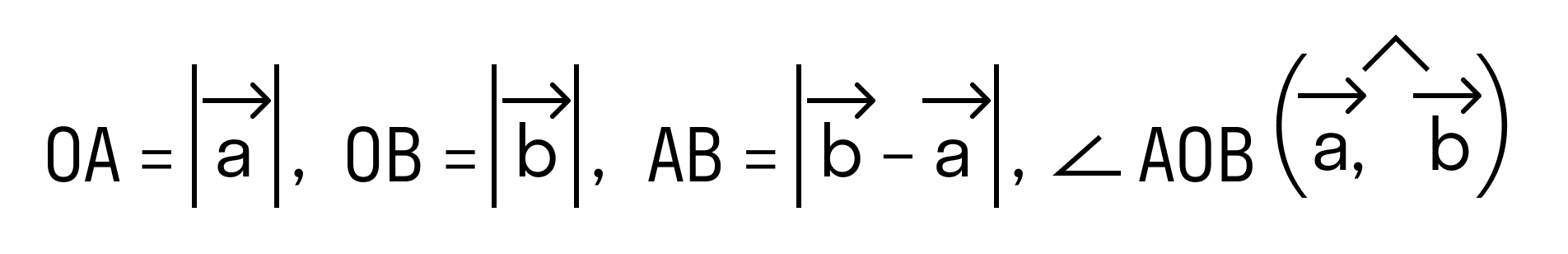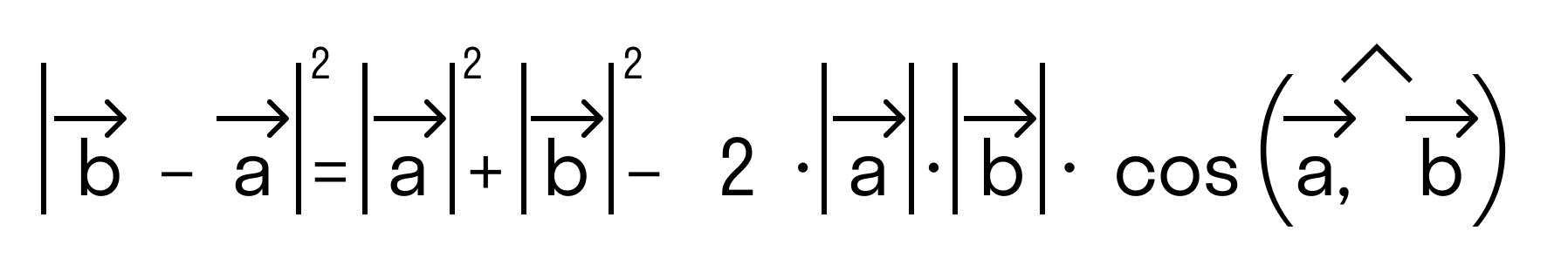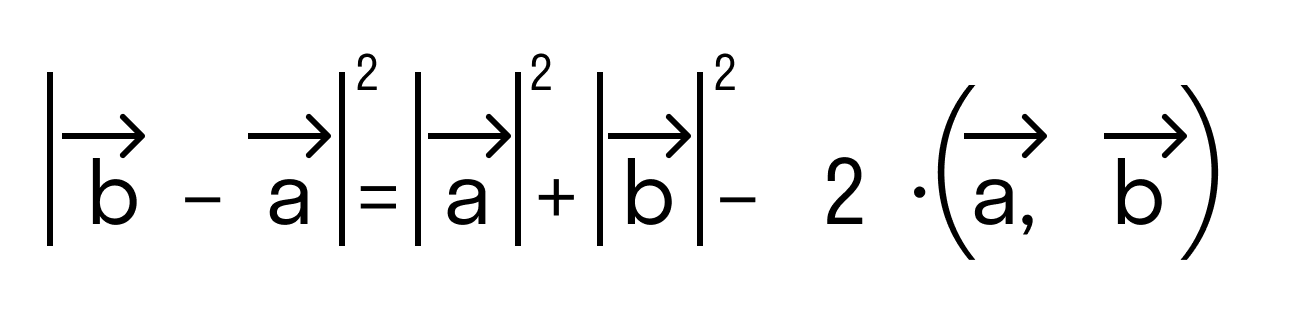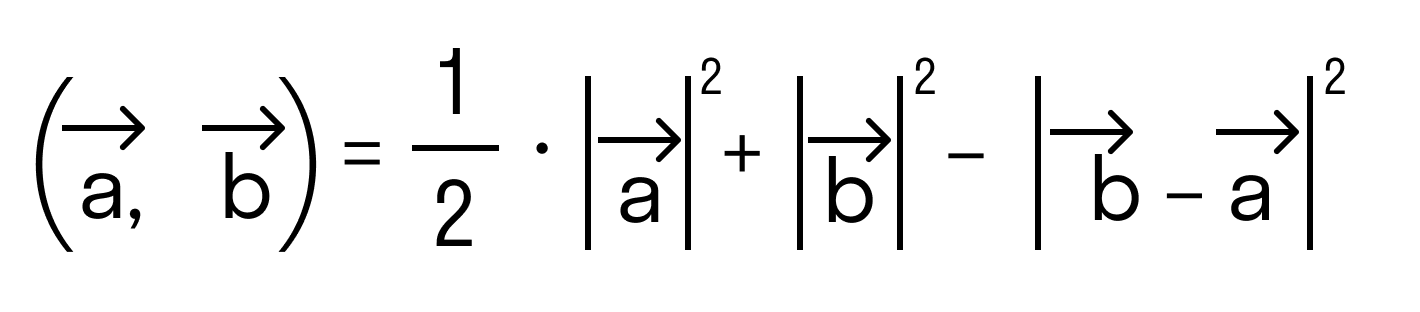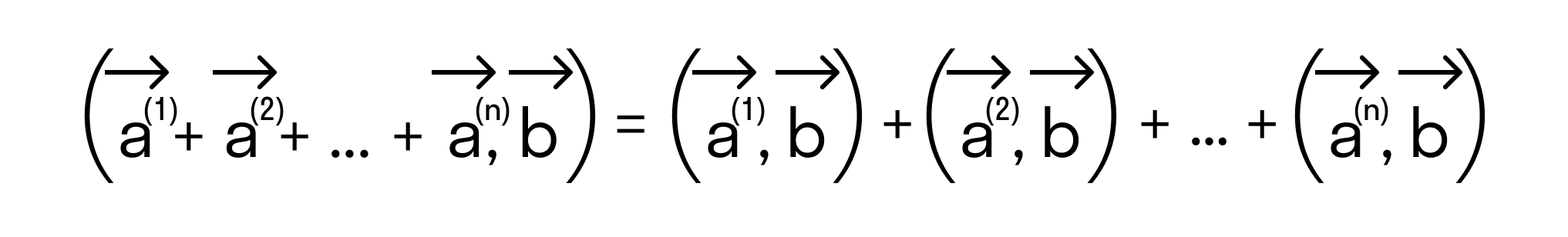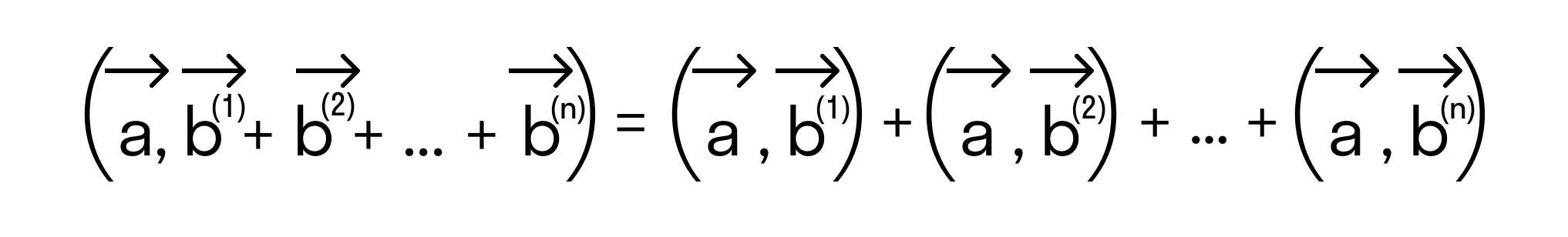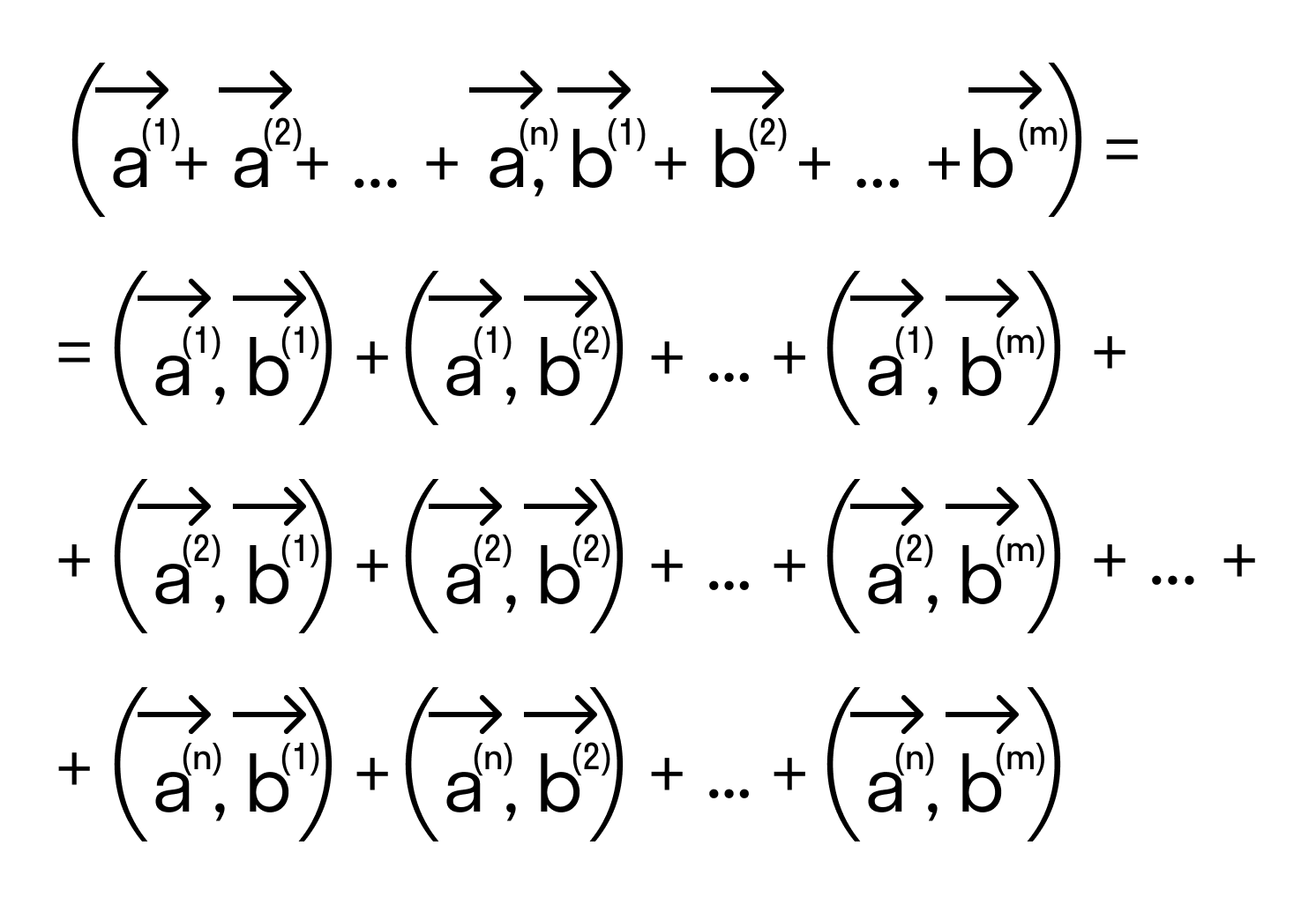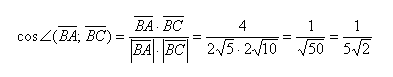Что можно сказать о векторах координаты которых равны а1 а2 а3 и ка1 ка2 ка3

1. Какая величина называется векторной (или просто вектором)?

Физическая величина, которая характеризуется не только числовым значением (модулем), но и направлением, называется векторной величиной (или просто вектором).
Для векторной величины одинаково важны числовое значение (модуль) и направление.

Примеры векторных величин:

— скорость,
— перемещение,
— сила.

2. Какая величина называются скалярной (или просто скаляром)?

Величины, которые не имеют направления и задаются только числом, называются скалярными величинами или скалярами.

Примеры скалярных величин:

— число книг на полке,
— длина карандаша,
— высота комнаты.
Модуль вектора — тоже скаляр.

3. Как изображают векторную величину?

Векторную величину изображают в виде стрелки, которая начинается в некоторой точке и заканчивается острием, указывающим направление..
Такой отрезок-стрелка называется вектором.
Длина стрелки в выбранном масштабе выражает модуль векторной величины.

Векторы обозначают буквами со стрелкой над ними.
Такой же буквой, но без стрелки обозначают модуль вектора.

4. Если два вектора равны друг другу по модулю, но направления векторов различны, то можно ли сказать, что эти векторы равны друг другу?

Нет, нельзя.
Равными считаются векторы, у которых одинаковы и модули, и направления.

5. Чем отличается векториая величина от скалярной?

Векторная величина характеризуется модулем (величиной) и направлением, а скалярная величина — только модулем.
Вектор имеет направление, а скаляр не имеет направления.

Проекция вектора на координатную ось

1. Как построить проекцию вектора на координатную ось?

Есть вектор а.
Опустим из точки А (начало вектора) и точки В (конец вектора) перпендикуляры на ось ОX.
Получим на оси точки х_а и х_в — это проекции точек А и В на ось ОX.
Длину отрезка х_а-х_в между проекциями начала и конца вектора называют проекцией вектора а на ось ОX и обозначают, как а_х.
Проекцию вектора на ось обозначают той же буквой, что и вектор, но без стрелки и с индексом оси.
Проекция вектора — величина скалярная.

2. Если вектор перемещения параллелен координатной оси, то чему равен модуль проекции вектора на эту ось?

Если вектор параллелен оси координат, то модуль его проекции ( |a_x| ) равен модулю ( a ) самого вектора.

3. Что называют проекцией вектора на координатную ось?

Длину отрезка на координатной оси между проекциями начала и конца вектора, взятую со знаком « + » или « —», называют проекцией вектора а на координатную ось.

3. Когда проекция вектора на ось будет положительной, а когда — отрицательной?

Проекция вектора на координатную ось может быть, как положительной, так и отрицательной.

Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью.
Проекция вектора на ось считается отрицательной, если вектор направлен противоположно оси.

Если вектор перпендикулярен координатной оси, то при любом направлении вектора его проекция на ось равна нулю.

Видео:9 класс, 2 урок, Координаты вектораСкачать

Скалярное произведение векторов

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

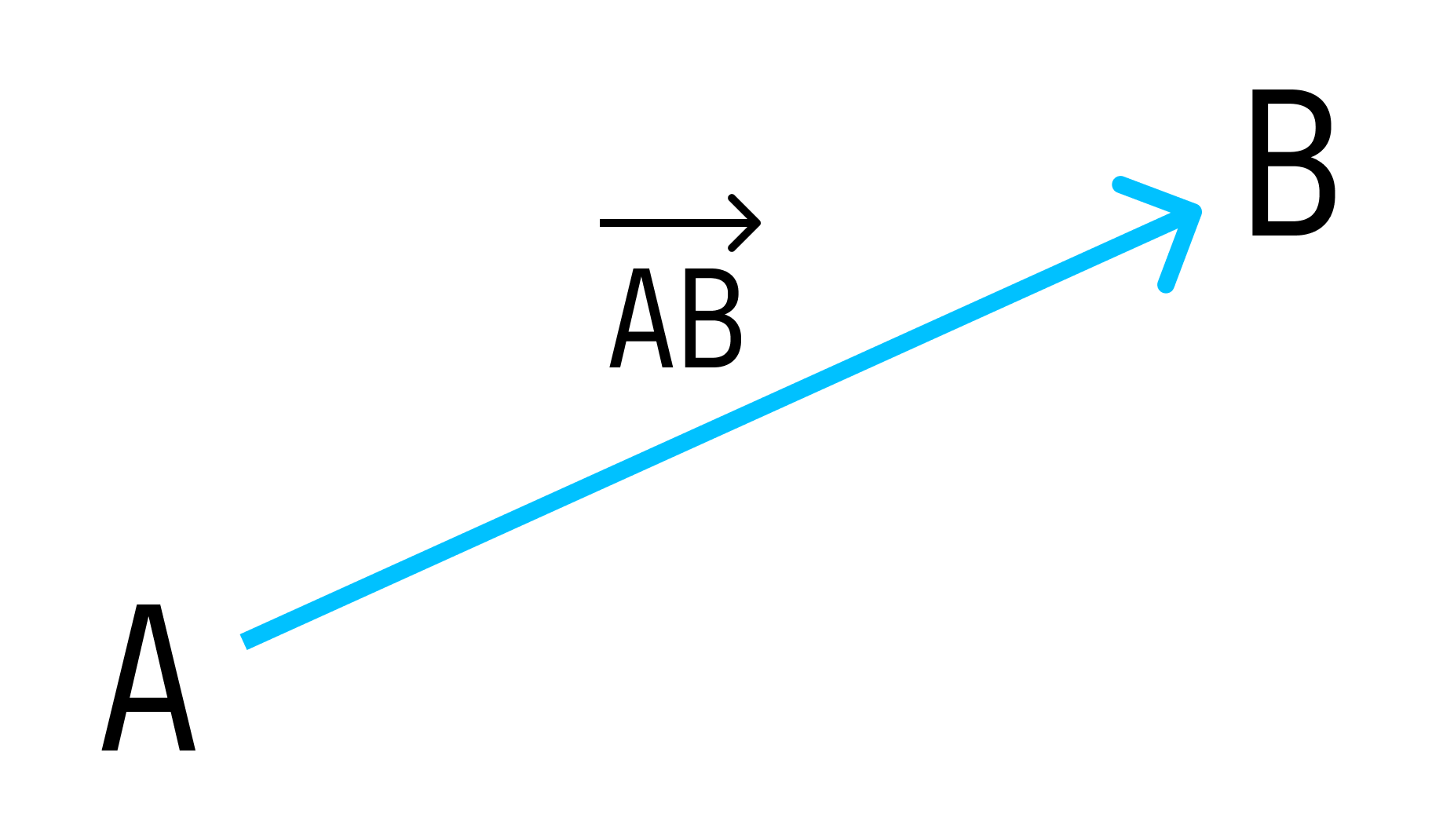
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

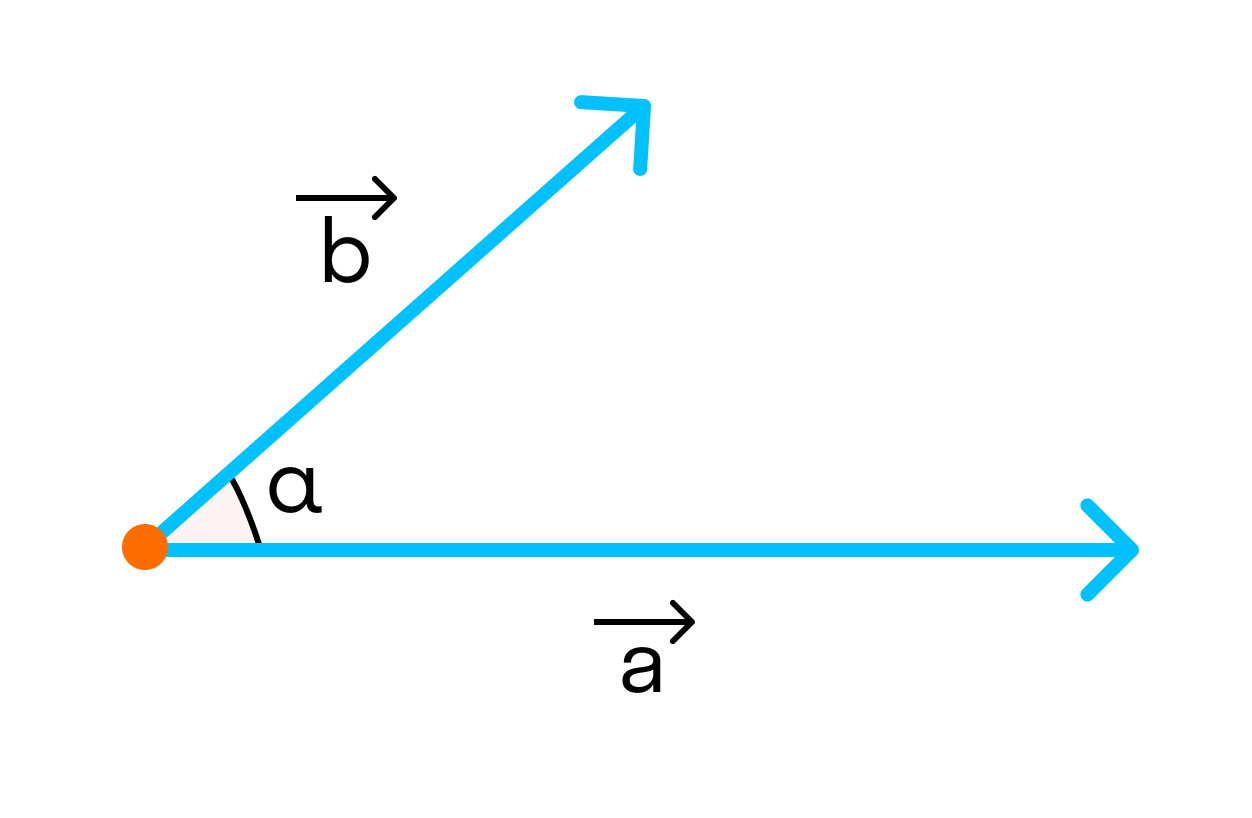
Угол между векторами

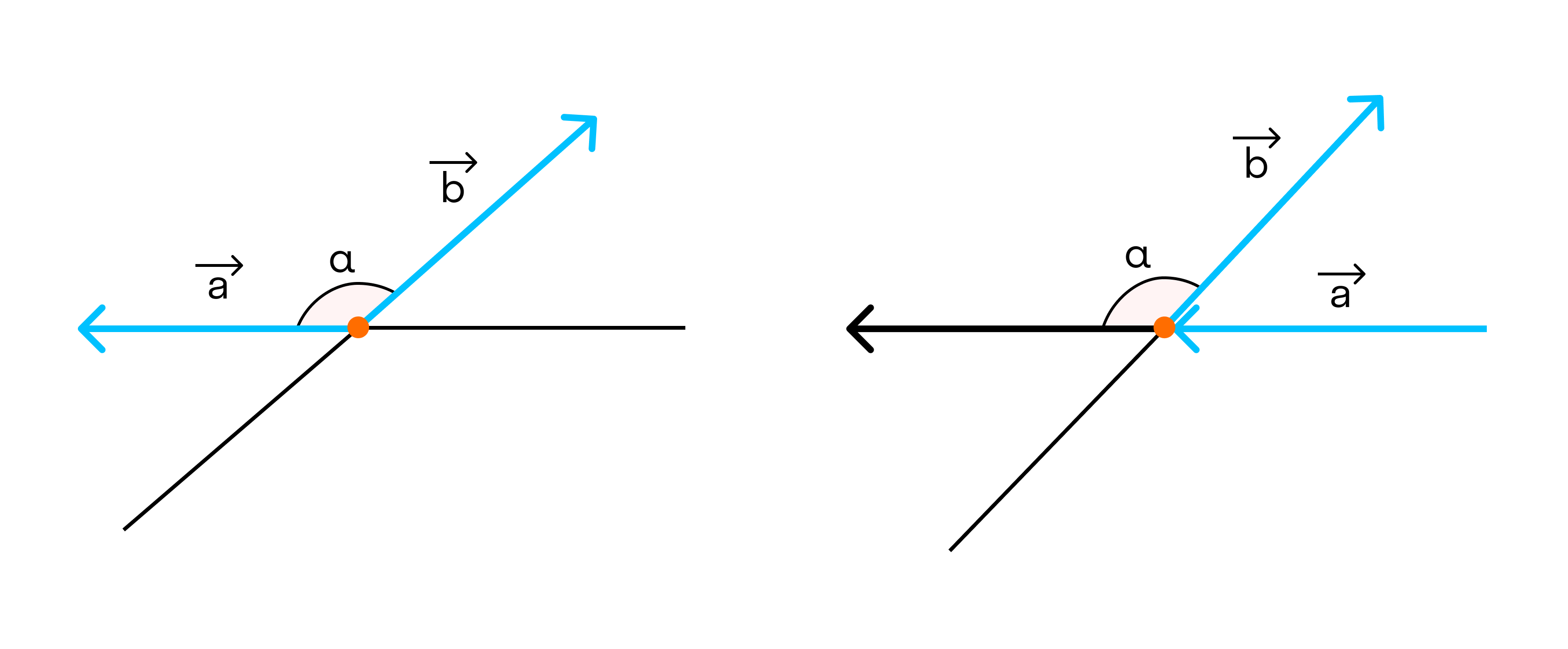
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=

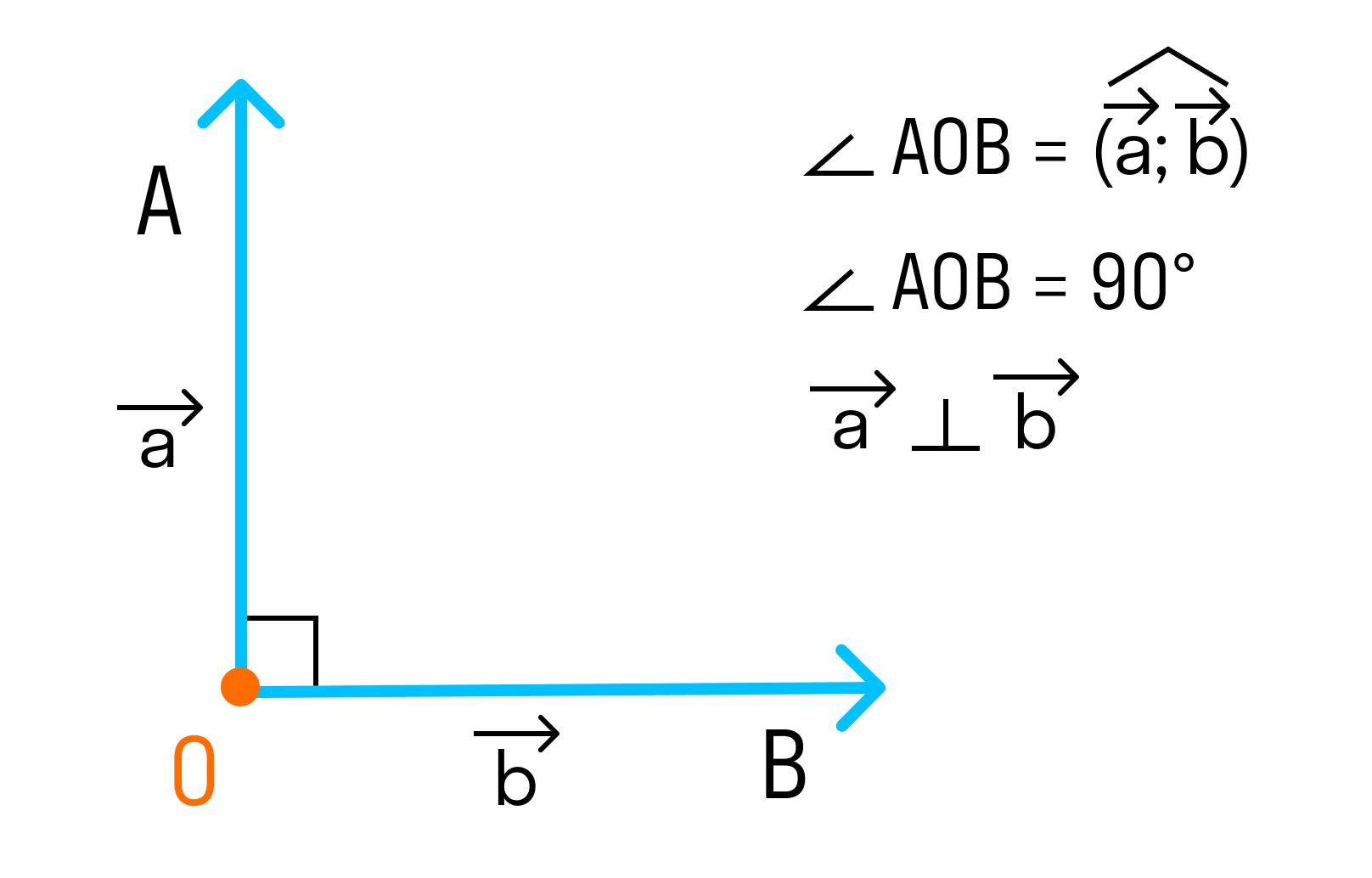
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

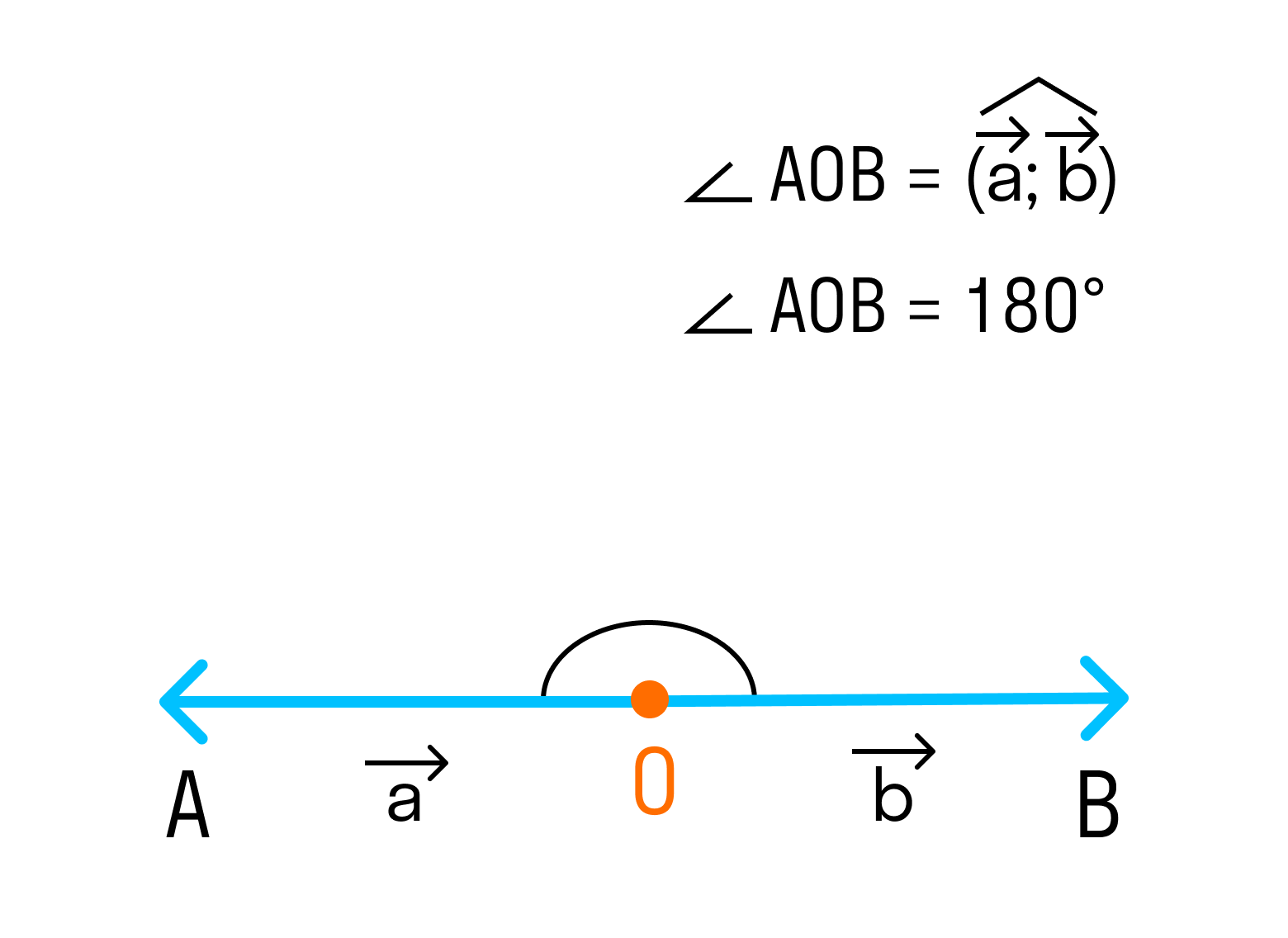
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.

Также векторы могут образовывать тупой угол. Это выглядит так:

Видео:Координаты вектора | Геометрия 7-9 класс #86 | ИнфоурокСкачать

Скалярное произведение векторов

Определение скалярного произведения можно сформулировать двумя способами:

Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.

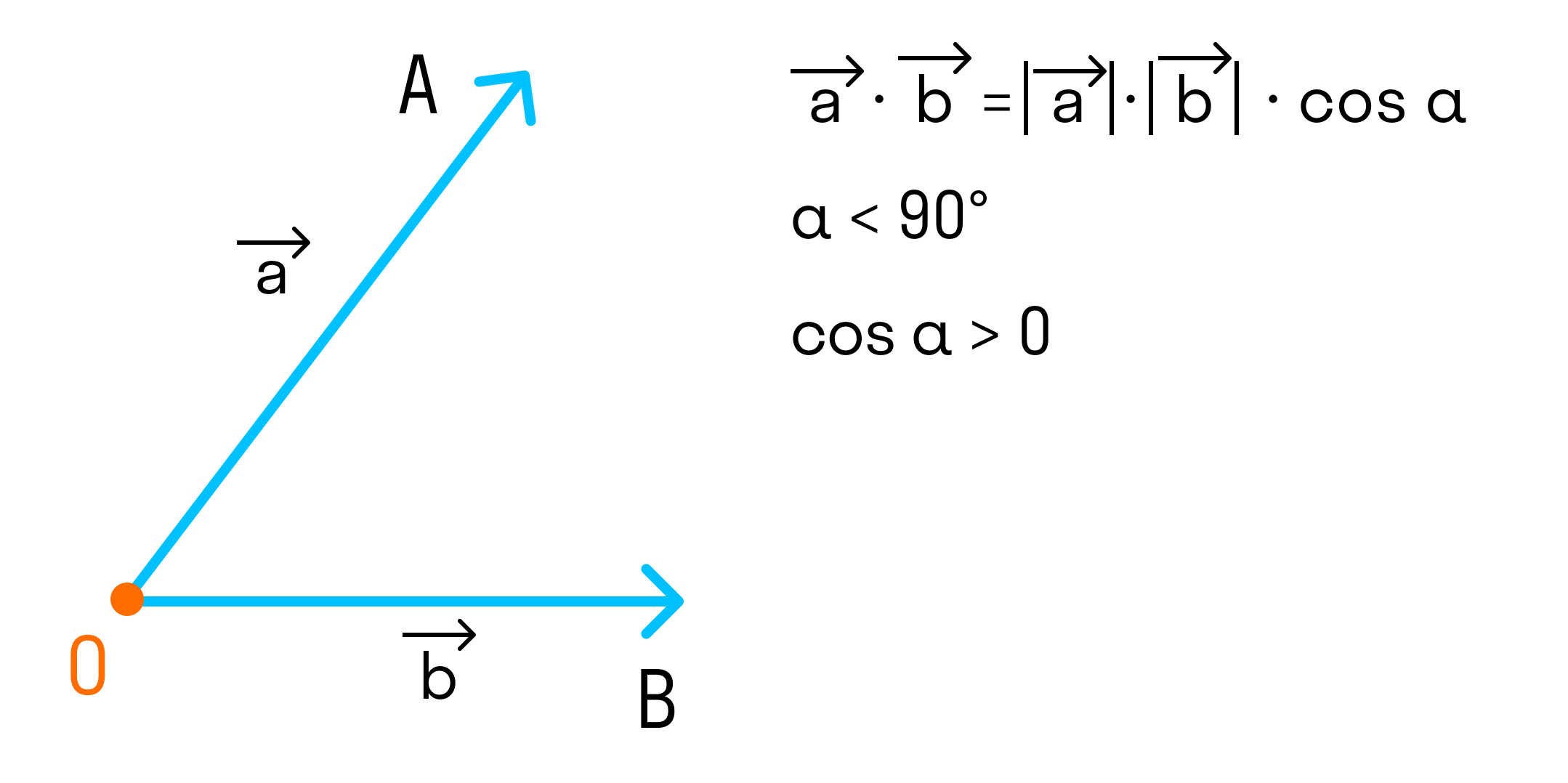
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

→a * →b = →|a| * →|b| * cosα

Что важно запомнить про геометрическую интерпретацию скалярного произведения:

• Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
• Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Скалярное произведение в координатах

Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.

То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by

А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz

Докажем это определение:

Сначала докажем равенства

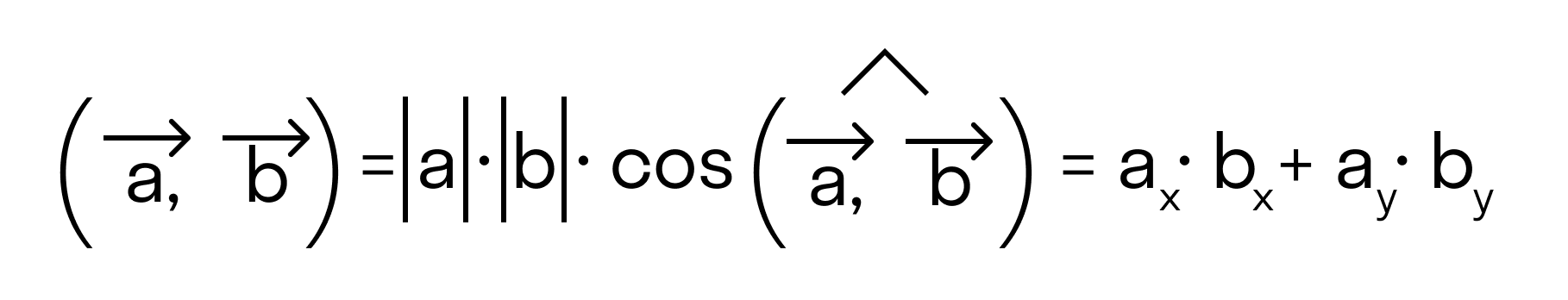
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)

Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)

Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:

то последнее равенство можно переписать так:

а по первому определению скалярного произведения имеем

Вспомнив формулу вычисления длины вектора по координатам, получаем

Записывайтесь на наши курсы по математике для учеников с 1 по 11 классы!

Видео:Координаты вектора. 9 класс.Скачать

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В плоской задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by

Формула скалярного произведения векторов для пространственных задач

В пространственной задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by + az * bz

Формула скалярного произведения n-мерных векторов

В n-мерном пространстве скалярное произведение векторов a = и b = можно найти по формуле:

a * b = a1 * b1 + a2 * b2 + . + an * bn

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Свойства скалярного произведения

Свойства скалярного произведения векторов:

Скалярное произведение вектора самого на себя всегда больше или равно нулю. В результате получается нуль, если вектор равен нулевому вектору.

→0 * →0 = 0

Скалярное произведение вектора самого на себя равно квадрату его модуля:

→a * →a = →∣∣a∣∣2

Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:

→a * →b = →b * →a

Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:

(→a + →b) * →c = →a * →c + →b * →c

Сочетательный закон для скалярного произведения:

(k * →a) * →b = k * (→a * →b)

Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:

a ≠ 0, b ≠ 0, a * b = 0 a ┴ b

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)

По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.

Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Примеры вычислений скалярного произведения

Пример 1.

Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

У нас есть все данные, чтобы вычислить скалярное произведение по определению:

(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.

Ответ: (→a,→b) = 21/2 = 10,5.

Пример 2.

Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.

Используем формулу →a * →b = →|a| * →|b| * cosα.

В данном случае:

→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3

Пример 3.

Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.

По свойству дистрибутивности скалярного произведения имеем

Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:

В силу свойства коммутативности последнее выражение примет вид

Итак, после применения свойств скалярного произведения имеем

Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:

Пример 4.

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.

Введем систему координат.

Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.

Найдем координаты векторов →AB1 и →BC1:

Найдем длины векторов →AB1 и →BC1:

Найдем скалярное произведение векторов →AB1 и →BC1:

Найдем косинус угла между прямыми AB1 и BC1:

Пример 5.

а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .

б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).

а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно

б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)

Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.

Обратите внимание на два существенных момента:

• В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
• В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.

Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.

Пример 6.

Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.

По условию чертеж выполнять не требуется, но для удобства можно сделать:

Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.

Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).

Вычислим скалярное произведение:

Вычислим длины векторов:

Найдем косинус угла:

Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:

Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.

Найдём сам угол:

Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.

Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°

Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.

А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Геометрия. 9 класс

Конспект
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором.
Положение вектора на плоскости задаётся его координатами. Для определения координат вектора нужно уметь раскладывать данный по координатным векторам.
Покажем, что любой вектор можно разложить по неколлинеарным векторам.
Но сначала рассмотрим лемму о коллинеарных векторах. Такие вектора могут быть либо сонаправленны, либо противоположно направлены.
Рассмотрим каждый случай.
Докажем первый случай, когда векторы a и b сонаправлены.
Возьмем число k равное отношению длин заданных векторов: k = |b ⃗|/|a ⃗|
Так как k неотрицательное число, то: |ka ⃗| = |k| ∙ |a ⃗| = |b ⃗|/|a ⃗| ∙ |a ⃗| = |b ⃗|
Следовательно, эти векторы равны: |b ⃗| = |ka ⃗|
Рассмотрим второй случай, когда векторы а и b противоположно направлены.
Возьмем число k равное отношению длин этих векторов со знаком минус:
k = -|b ⃗|/|a ⃗|
Так как k число отрицательное, то векторы снова сонаправлены. Также убеждаемся в том, что их длины равны:
Поэтому векторы равны:
Лемма доказана.
Теперь докажем, что любой вектор может быть разложен по двум неколлинеарным векторам.
Формулировка теоремы звучит так: на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Докажем сначала, что любой вектор p можно разложить по векторам а и b
Возможны два случая:
1) Вектор р коллинеарен одному из векторов а и b, например вектору b.
Тогда по лемме о коллинеарных векторах вектор p можно представить в виде, где y некоторое число.
И, следовательно, вектор p разложен по векторам а и b
2) Вектор р не коллинеарен ни вектору а, ни вектору b.
Тогда мы отметим какую-нибудь точку О и отложим от нее неколлинеарные векторы, равные данным векторам

Введем для векторов обозначения:
— вектор OB равен вектору b
— вектор ОР равен вектору р
— вектора ОА равен вектору а
Через точку Р проведем прямую, параллельную прямой ОВ. Обозначим точку пересечения этой прямой с прямой ОА точкой А₁. По правилу треугольника вектор р можно представить в виде суммы векторов ОА₁ и А₁Р. Так как векторы ОА₁ и А₁Р коллинеарны соответственно векторам а и b.
Следовательно, любой вектор можно разложить по двум данным неколлинеарным векторам
(p) ⃗ = (ОА₁) ⃗+ (А₁ Р) ⃗
(ОА₁) ⃗= ха ⃗
(А₁ Р) ⃗= уb ⃗
p ⃗= xa ⃗+ yb ⃗
Далее мы докажем, что коэффициенты разложения x и y определяются единственным образом.
Допустим, что существует другое разложение вектора p и запишем новые коэффициенты разложения обозначив их с индексом 1.
p ⃗= xa ⃗+ yb ⃗
p ⃗= x₁ a ⃗+ y₁ b ⃗
Вычитая второе равенство из первого и используя правила действий над векторами, получаем p ⃗- p ⃗= (xa ⃗+ yb ⃗) — (x₁ a ⃗+ y₁ b ⃗)
0 ⃗= xa ⃗+ yb ⃗- x₁ a ⃗- y₁ b ⃗
0 ⃗= (x — x₁)a ⃗+ (y — y₁)b ⃗
Выразим один из векторов. Например, вектор а: a ⃗= -(y — y₁)/(x — x₁) b ⃗
Это значит, что векторы а и b коллинеарны.
Но это противоречит условию теоремы. То есть коэффициенты определяются единственным образом и теорема доказана.
Введем понятие координаты вектора c помощью прямоугольной системы координат и рассмотрим правила, позволяющие находить сумму, разность и произведение вектора на число по координатам векторов, без геометрически построений.
Отложим от начала координат единичные векторы.
Эти векторы называются координатными векторами.
Координатные векторы не коллинеарны, поэтому любой вектор p можно разложить по координатным векторам единственным образом. Координаты вектора записываются в фигурных скобках после обозначения вектора: p ⃗
Рассмотрим правила сложения, вычитания и умножения вектора на число по координатам векторов.
Первое правило – правило сложения: каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов
Докажем это утверждение. Пусть векторы а и b заданы своими координатами:
а ⃗<х₁; у₁>
b ⃗<х₂; у₂>
Это значит, что разложение данных векторов по координатным осям выглядит следующим образом:
а ⃗= х₁ i ⃗+ y₁ j ⃗
b ⃗= х₂ i ⃗+ y₂ j ⃗
Используя свойства сложения и умножения вектора на число получим:
а ⃗+ b ⃗= х₁ i ⃗+ y₁ j ⃗+ х₂ i ⃗+ y₂ j ⃗= (х₁ + х₂)i ⃗ + (y₁ + y₂)j ⃗
Это и значит, что координаты вектора а плюс b, равны сумме соответствующих координат: а ⃗+ b ⃗<х₁ + х₂; y₁ + y₂>
Утверждение о том, что каждая координата разности двух векторов равна разности соответствующих координат этих векторов, доказывается аналогично.
а ⃗<х₁; у₁>
b ⃗<х₂; у₂>
а ⃗- b ⃗<х₁ — х₂; y₁ — y₂>
И последнее правило – правило определения координат вектора при умножении его на число, звучит следующим образом: каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
а ⃗<х; у>
(kа) ⃗<kх; kу>

🔍 Видео

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Координаты точки и координаты вектора 1.Скачать

Все о векторах за 60 минут | Математика ОГЭ | Молодой РепетиторСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Координаты вектора. Видеоурок по геометрии 9 классСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Скалярное произведение векторов. 9 класс.Скачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

ВЕКТОРЫ на плоскости: координаты, длина, равенство вектора, определение коллинеарности векторовСкачать