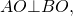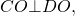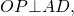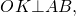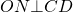Видео:Где центр окружности? ТрапецияСкачать
Ваш ответ
Видео:Геометрия Точка O центр окружности вписанной в треугольник ABC BC = a AC = b угол AOB = 120 НайдитеСкачать
решение вопроса
Видео:Найдите площадь вписанной трапеции ABCD, если BC=4см, ∠BCD=30о и точка O центр окружности.Скачать
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,049
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Геометрия В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружностиСкачать
Подскажите решить пожалуйста, прошуууу
3. На рис.133 АВСD -трапеция, точка О – центр вписанной окружности, ОЕ=6см, ВС=10 см, DE=9 см. Найдите периметр трапеции.
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. (свойство).
ОЕ⊥СD⇒ ОЕ — радиус.
АВ⊥ВС и АD
Проведем OK⊥АВ
OH ⊥ AD
АН=ОК=OE=6
AD=AH+HD=15
Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.
ВС+AD=AB+CD
Р=ВС+AD+AB+CD=2•(10+15)=50 см
4. На рис. 134 точка О – центр вписанной окружности, угол А=углу С, BD=18 см, BO:OD=5:4. Найдите стороны треугольника.
х=18:9=2
По условию углы при АС равны. ⇒ ∆ АВС — равнобедренный, АВ=ВС.
Центр вписанной в треугольник окружности лежит на биссектрисе.
Биссектриса равнобедренного треугольника — высота и медиана. ⇒
∠BDA=90°
AD=CD.
Проведем ОН — перпендикуляр в точку касания на АВ.
Из ∆ ВОН по т.Пифагора ВН=6
В прямоугольных ∆ АВD и ∆ OBH острый угол при В общий. ⇒
Из подобия следует отношение
АВ:ВО=ВD:BH
AB=180:6=30
По т.Пифагора AD=24 ⇒
АС=48
ВС=АD=30
Видео:Геометрия Центр окружности, вписанной в равнобокую трапецию, удален от концов ее боковой стороныСкачать
Вписанная в трапецию окружность
Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?
1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.
1) В трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.
2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.
O — точка пересечения
биссектрис трапеции ABCD.
3. По свойству биссектрис трапеции, прилежащие к её боковой стороне,
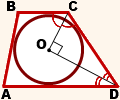
и точка O лежит на средней линии трапеции.
4. Точки касания, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины:
5.
6. Диаметр вписанной в трапецию окружности равен высоте трапеции, радиус — половине высоты:
🎬 Видео
Задача про трапецию, описанную около окружностиСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
ОГЭ без рекламы математика 17 вариант задача 25Скачать
Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать
Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать
ОГЭ ЗАДАНИЕ 16 РАДИУС ОКРУЖНОСТИ ВПИСАННОЙ В ТРАПЕЦИЮ РАВЕН 18. НАЙДИТЕ ВЫСОТУ ЭТОЙ ТРАПЕЦИИСкачать
Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать
4.43.1. Планиметрия. Гордин Р.К.Скачать
10 класс, 31 урок, Пространственная теорема ПифагораСкачать
Окружность, вписанная в трапециюСкачать
8 причин прокрастинации - советы для студентов и школьников от лектора с физтехаСкачать
Почему любая вписанная трапеция будет равнобедренной? #геометрияегэСкачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
