Четырехугольник описан около окружности с центром о докажите что аов сод 180

Геометрия | 5 — 9 классы

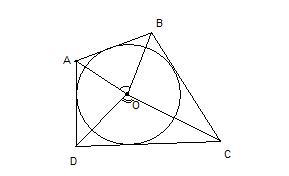
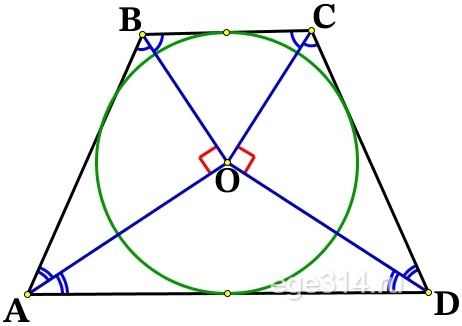
Докажите, что если в четырехугольник АВСД вписана окружность с центром в точке О, то угол АОВ + угол СОД = 180 градусов.

Рассмотрим треугольник АОВ.

Здесь &lt ; OAB = 1 / 2&lt ; A.

Для этого утверждения мы использовали свойство касательных к окружности : отрезки касательных АВ и АD к окружности, проведенные из одной точки А, равны и составляют равные углы с прямой АО, проходящей через эту точку А и центр окружности О (&lt ; OAB = &lt ; OAD = 1 / 2&lt ; A).

Таким же образом утверждаем, что&lt ; ОВА = 1 / 2&lt ; В (касательные ВС и ВА проведены к окружности из точки В).

Зная сумму углов треугольника, запишем :

&lt ; AOB = 180 — (&lt ; OAB + &lt ; OBA) = 180 — (1 / 2&lt ; A + 1 / 2&lt ; B) = 180 — 1 / 2(&lt ; A + &lt ; B).

Рассмотрим треугольник COD.

Здесь &lt ; OCD = 1 / 2&lt ; C (касательные CB и CD к окружности проведены из точки С) и &lt ; ODC = 1 / 2&lt ; D (касательные DC и DA проведены из точки D).

&lt ; COD = 180 — (&lt ; OCD + &lt ; ODC) = 180 — (&lt ; 1 / 2&lt ; C + 1 / 2&lt ; D) = 180 — 1 / 2(&lt ; C + &lt ; D).

Зная сумму углов четырехугольника ABCD, запишем :

&lt ; A + &lt ; B + &lt ; C + &lt ; D = 360,

&lt ; A + &lt ; B = 360 — &lt ; C — &lt ; D.

В выражение &lt ; AOB = 180 — 1 / 2(&lt ; A + &lt ; B) подставим значение для суммы &lt ; A + &lt ; B :

&lt ; AOB = 180 — 1 / 2(&lt ; A + &lt ; B) = 180 — 1 / 2(360 — &lt ; C — &lt ; D) = 1 / 2(&lt ; C + &lt ; D).

Запишем сумму углов АОВ и COD :

&lt ; AOB + &lt ; COD = 1 / 2(&lt ; C + &lt ; D) + 180 — 1 / 2(&lt ; C + &lt ; D) = 180°, что и требовалось доказать.

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Четырехугольник АВСД вписан в окружность?

Четырехугольник АВСД вписан в окружность.

Угол АВС равен 48 градусов, угол САД равен 38 градусов.

Найдите угол АВД.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Четырехугольник АВСД вписан в окружность?

Четырехугольник АВСД вписан в окружность.

Угол Авс равен 130 градусов, угол САД равен79 град.

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

В угол С велечиной 79 градусов вписана окружность с центром О которая касается сторон угла в точках А и В?

В угол С велечиной 79 градусов вписана окружность с центром О которая касается сторон угла в точках А и В.

Найдиде угол АОВ.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Чему равен угол угол АДС четырехугольника АВСД, вписанного в окружность, если угол АСД = 32 градуса, СВД = 56 градусов, САВ = 48 градусов?

Чему равен угол угол АДС четырехугольника АВСД, вписанного в окружность, если угол АСД = 32 градуса, СВД = 56 градусов, САВ = 48 градусов.

Видео:16) Четырехугольник АВСD описан около окружности, AD=7, DC=12, BC=13. Найдите AB. Математика огэ.Скачать

В угол с величиной 99 градусов вписана окружность с центром в точке О, которая касается сторон угла в точках А и В?

В угол с величиной 99 градусов вписана окружность с центром в точке О, которая касается сторон угла в точках А и В.

Найдите угол АОВ.

Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности?

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности.

Найдите угол АОВ.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности?

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности.

Найдите угол АОВ.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

В угол с величиной 75° вписана окружность которая касается сторон угла в точках А и В где о — центр окружность?

В угол с величиной 75° вписана окружность которая касается сторон угла в точках А и В где о — центр окружность.

Найти угол АОВ ответ дать в градусах.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Треугольник ABC вписан в окружность с центром в точке О Найдите ACB если угол АОВ равен 173 градуса?

Треугольник ABC вписан в окружность с центром в точке О Найдите ACB если угол АОВ равен 173 градуса.

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Точка О — центр вписанной в треугольник АВС окружности найти угол С , если угол АОВ равен 128 градусам?

Точка О — центр вписанной в треугольник АВС окружности найти угол С , если угол АОВ равен 128 градусам.

Вы перешли к вопросу Докажите, что если в четырехугольник АВСД вписана окружность с центром в точке О, то угол АОВ + угол СОД = 180 градусов?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Обозначения : c — содержится ą — альфа Пусть МК — средняя линия трапеции. = > МК||ВС, ВС с ą = > MK||ą (Если прямая, не лежащая в данной плоскости, параллельна какой — нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости) Сред..

Ответ смотри на фото. Сорри, что карандашом, ручки под рукой не оказалось. В дано под цифрами написано то, что сказано только в одном из случаев. В решении — решение вопроса.

4) 180 — 45 = 135 5)180 — 40 — 90 = 50 7)90 т. К. угол прямой 8)ответ 40 т. К. угол DBЕ вертикален углу СBА.

Одну и только одну. Все три точки лежат на одной прямой.

Если три точки лежат на одной прямой, то другую провести нельзя (Ответ — одну прямую).

Б) 4 Т. К. каждая сторона треугольника должна быть меньше суммы двух других. Г)1 — не подходит, т. К. сказано, что длина не меньше 4.

УГОЛ cad = 30 следовательно угол bad = 30 (т. К. ad — биссектриса) угол А = 30 + 30 = 60 градусов угол А + угол В + угол С = 180 по теореме о сумме углов в треугольнике угол В = 180 — угол С — угол А угол В = 180 — 60 — 50 = 70 градусов ответ : угол..

АД биссектриса, значит делит угол пополам. ЦАД половина, значит весь угол А будет равен 2 ЦАД равен 60. Сумма всех углов в треуг. 180. Значит угол Б равен 180 — 50 — 60 = 70.

Видео:11 класс, 43 урок, Вписанный четырехугольникСкачать

Четырёхугольник ABCD описан около окружности, с центром в точке О. Докажите, что сумма градусных мер углов: a)AOB и COD; 6)BOC и AOD равна 180°.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Ваш ответ

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,739
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

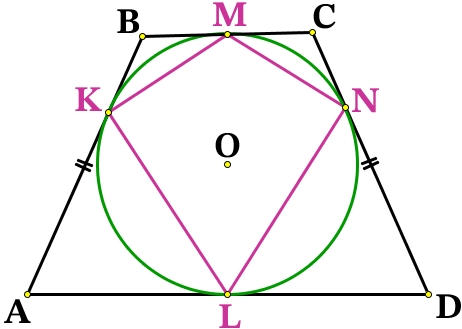
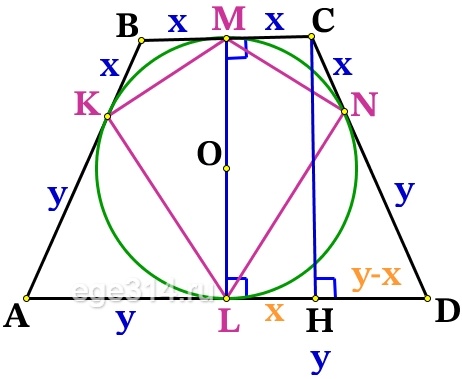
Решение №2583 Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

а) Докажите, что треугольник АОВ прямоугольный.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac площади трапеции ABCD.

Источник: Ященко ЕГЭ 2022 (36 вар)

а) Доказать , что в ΔАОВ ∠АОВ = 90° (тогда он прямоугольный) .

Окружность вписана в углы: ∠ВAD, ∠ADC, ∠DCB и ∠CBA. Центр окружности, которая вписана в угол, расположен на биссектрисе этого угла, значит АО, DO, СО, ВО – биссектрисы и делят соответствующие углы пополам.

∠ВAD + ∠CBA = 180°
∠ADC + ∠DCB = 180°

Как односторонние углы, при параллельных прямых AD||ВС (основания трапеции) и секущих AB и СD соответственно.
Зная о биссектрисах поделим всё на 2:

Рассмотрим треугольники ΔАВО и ΔDCO, сумма углов любого треугольника равна 180°, тогда:

∠AOB = ∠COD = 90°

Что и требовалось доказать.

б) Найти: frac , если АВ = СD, S_=fraccdot S_ :

Отрезки касательных к окружности, проведённые из одной точки, равны:

BM = BK
CM = CN
AK = AL
DL = DN

Т.к. AB = CD, то:

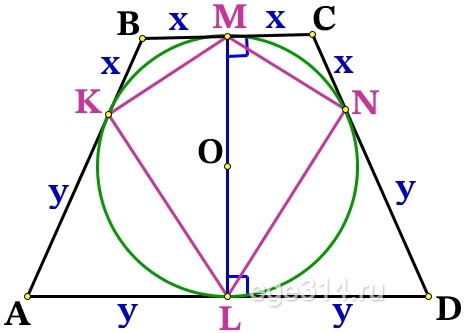
BK = СN = BM = CM = x
AK = DN = AL = DL = y

Проведём радиусы из точки О к касательным ВС и AD, тогда ОМ⊥ВС, OL⊥AD, точка О∈OM, O∈OL, значит МL это одна прямая и высота трапеции:

Проведём ещё одну высоту трапеции СН:

MC = LH, МCHL – прямоугольник, значит MC = LH = x , найдём HD:

HD = LD – LH = y – x

Из прямоугольного ΔСHD по теореме Пифагора найдём СН:

СН 2 + HD 2 = CD 2
CH 2 + (y – x) 2 = (y + x) 2
CH 2 = (y + x) 2 – (y – x) 2 = y 2 + 2xy + x 2 – y 2 + 2xy – x 2 = 4xy
CH=sqrt=2sqrt

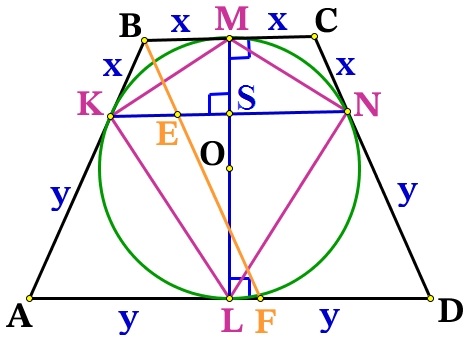
Выразим площадь S_{ABCD :}

В четырёхугольнике проведём KMNL диагональ KN, прямые ВС и KN отсекают равные отрезки ВК = СN = x, значит они по теорема Фалеса параллельны ВС||KN, т.к. BC⊥LM, то KM⊥ML, значит угол между диагоналями ∠MSK = 90°.
Диагональ ML = 2sqrt , как высота трапеции.
Проведём BF||CD и пересекающая KN в точке Е. BCDF – параллелограмм, значит EN = BC = 2x.

ΔАВF подобен ΔВКЕ (∠В – общий, ∠ВКЕ = ∠ВАF – соответственные). Из пропорциональности сторон найдём КЕ:

Найдём диагональ KN:

Выразим площадь S_KMNL :

S_=fraccdot MLcdot KNcdot sin angle MSK=fraccdot 2sqrtcdot fraccdot sin 90^=sqrtcdot fraccdot 1= frac<4xysqrt>

Подставим выраженные площади с исходное отношение:

Т.к. у нас у большее основание, а х меньшее, то их отношение равно 8.

📺 Видео

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

2175 AC и BD диаметры окружности с центром О угол acb равен 35 Найдите угол aodСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

11 класс, 44 урок, Описанный четырехугольникСкачать

Тема 9. Вписанные и описанные четырехугольникиСкачать