Как правильно писать углы треугольника

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Угол. Обозначение углов

Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

На рис. 1 лучи АВ и АС — стороны угла, точка А — вершина угла.

При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: ВАС или САВ (этот угол нельзя обозначить так: АВС или СВА или ВСА или АСВ, т.к. точки В и С не являются вершинами данного угла). Этот же угол можно обозначить и короче, по его вершине: А.

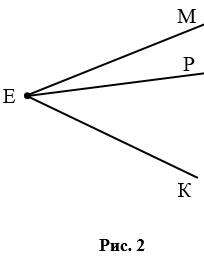
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: МЕК или КЕМ, МЕР или РЕМ, РЕК или КЕР. Говорят, что луч ЕР в данном случае делит угол МЕК (или КЕМ) на два угла: МЕР (или РЕМ) и РЕК (или КЕР).

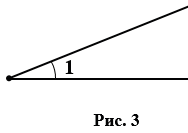
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 1.

Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Если при наложении одного угла на другой они совпадут, то эти углы равны.

Биссектриса — луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ — биссектриса угла НОD.

Прямой угол — угол, который можно построить с помощью угольника (рис. 5).

Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.

На рис. 6 АОВ и ВОС — прямые, АОС — развернутый.

Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.

Острый угол — угол, который меньше прямого угла. На рис. 7 МОN — острый.

Тупой угол — угол, который больше прямого угла, но меньше развернутого. На рис. 8 РЕК — тупой.

Поделись с друзьями в социальных сетях:

Видео:КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Как написать углы треугольника

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Треугольник

Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:

Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:

В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.

Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак . Так, запись ABC будет читаться: треугольник ABC .

У каждого треугольника 3 вершины, 3 стороны и 3 угла.

Видео:Внешний угол треугольникаСкачать

Высота

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.

Отрезок BN — это высота ABC. Отрезок EL высота DEF, опущенная на продолжение стороны DF.

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.

Каждый треугольник имеет три высоты.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Биссектриса

Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.

Отрезок BN — это биссектриса ABC.

Каждый треугольник имеет три биссектрисы.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Медиана

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.

Отрезок BN — это медиана ABC.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Как называются углы треугольника

Как называются углы треугольника? Ответ может зависеть от того, сколько углов имеется при вершине треугольника.

Если при вершине треугольника есть только один угол, то его можно назвать одной буквой, по названию вершины.

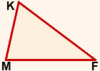
Например, в треугольнике MKF (рисунок 1) при каждой вершине есть только один угол. Следовательно, каждый из углов можно назвать одной буквой, по названию вершины, из которой исходят образующие этот угол лучи:

Угол M, угол K и угол F.

Для обозначения угла существует специальный знак: ∠

Запись ∠ M читают как «угол M».

Каждый из углов треугольника MKF можно назвать также тремя буквами. При этом вершина в названии угла должна стоять посередине.

Угол M также можно назвать углом KMF или углом FMK,

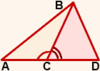
В треугольниках, изображенных на рисунке 2, одной буквой могут быть названы только углы при вершинах A и D: ∠A и ∠D.

При вершине B есть три угла, поэтому каждый из этих углов нужно назвать тремя буквами: ∠ABC, ∠CBD и ∠ABD.

Аналогично, углы при вершине C могут быть названы только тремя буквами: ∠ACB, ∠BCD и ∠ACD. Назвать какой-либо из этих углов ∠C нельзя.

Каждый из углов треугольников, изображенных на рисунке 3, может быть назван только тремя буквами.

Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Треугольник. Формулы и свойства треугольников.

Видео:7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать

Типы треугольников

По величине углов

По числу равных сторон

Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

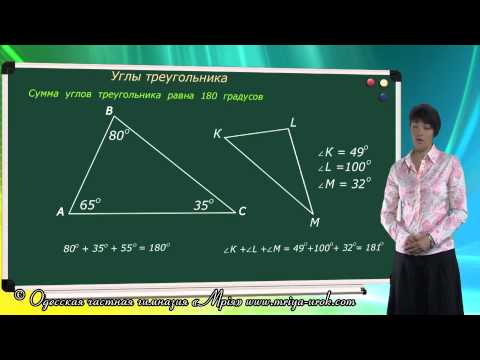
Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Видео:ВНЕШНИЕ УГЛЫ ТРЕУГОЛЬНИКА 😉 #shorts #математика #егэ #огэ #профильныйегэСкачать

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Видео:Углы треугольникаСкачать

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Связь между вписанной и описанной окружностями треугольника

Видео:Измерение угла с помощью транспортираСкачать

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Видео:Геометрия 7 класс (Урок№24 - Соотношения между сторонами и углами треугольника. Неравенство треуг.)Скачать

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Видео:Внешний угол треугольникаСкачать

Формулы площади треугольника

Формула Герона

Видео:7 класс. Соотношения между сторонами и углами треугольника.Скачать

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Треугольник

Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:

Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:

В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.

Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак . Так, запись ABC будет читаться: треугольник ABC .

У каждого треугольника 3 вершины, 3 стороны и 3 угла.

Высота

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.

Отрезок BN — это высота ABC. Отрезок EL высота DEF, опущенная на продолжение стороны DF.

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.

Каждый треугольник имеет три высоты.

Биссектриса

Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.

Отрезок BN — это биссектриса ABC.

Каждый треугольник имеет три биссектрисы.

Медиана

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.

Отрезок BN — это медиана ABC.