Годограф вектор функции решение задач

2-е изд., испр. — М.: 2002. — 144 с.

Предлагаемый сборник задач можно рассматривать как краткий курс векторного анализа, в котором сообщаются без доказательства основные факты с иллюстрацией их на конкретных примерах. Поэтому предлагаемый задачник может быть использован, с одной стороны, для повторения основ векторного анализа, а с другой — как учебное пособие для лиц, которые, не вдаваясь в доказательства тех или иных предложений и теорем, хотят овладеть техникой операций векторного анализа. При составлении задачника авторы использовали материал, содержащийся в имеющихся курсах векторного исчисления и сборниках задач. Значительная часть задач составлена самими авторами. В начале каждого параграфа приводится сводка основных теоретических положений, определений и формул, а также дается подробное решение 100 примеров. В книге содержится более 300 задач и примеров для самостоятельного решения. Все они снабжены ответами или указаниями к решению. Имеется некоторое количество задач прикладного характера, которые выбраны так, чтобы их разбор не требовал от читателя дополнительных сведений из специальных дисциплин. Материал шестой главы, посвященной криволинейным координатам и основным операциям векторного анализа в криволинейных координатах, внесен в книгу для того, чтобы дать читателю хотя бы минимальное количество задач для приобретения необходимых навыков. Сборник задач рассчитан на студентов дневных и вечерних отделений технических вузов, инженеров, а также на студентов-заочников, знакомых с векторной алгеброй и математическим анализом в объеме первых двух курсов.

ОГЛАВЛЕНИЕ
Главе 1. Вектор-фуикция скалярного аргумента . . . 3
§ 1. Годограф вектор-функции 3
§ 2. Предел и непрерывность вектор функции скалярного аргумента 5
§ 3. Производная вектор функции по скалярному аргументу . . 7
§ 4. Интегрирование вектор-функции скалярного аргумента . . 10
§ 5. Первая и вторая производные вектора по длине дуги кривой. Кривизна кривой. Главная нормаль 17
§ 6. Соприкасающаяся плоскость. Бинормаль. Кручение. Формулы Френе 19
Глава 2. Скалярное поле 23
§ 7. Примеры скалярных полей. Поверхности и линии уровня 23
§ 8. Производная по направлению 26
§ 9 Градиент скалярного поля . 29
Глава 3. Векторное поле 36
§ 10. Векторные линии. Дифференциальные уравнения векторных линий 36
§ 11. Поток векторного поля. Способы вычисления потока 41
1°. Поток векторного поля 41
2°. Способы вычисления потока вектора 44
§ 12. Поток вектора через замкнутую поверхность. Теорема Гаусса—Остроградского 60
§ 13. Дивергенция векторного поля. Соленоидальное поле — . 63
§ 14. Линейный интеграл от векторного поля. Циркуляция векторного поля . . 69
1. Свойства линейного интеграла 70
2. Вычисление линейного интеграла от векторного поля . 70
3°. Циркуляция векторного поля и ее вычисление 74
§ 15 Ротор (вихрь) векторного поля 77
§ 16. Теорема Стокса 79
§ 17. Независимость линейного интеграла от пути интегрирования. Формула Грина 82
Глава 4. Потенциальное поле 87
§ 18. Признаки потенциальности поля . . 87
§ 19 Вычисление линейного интеграла от потенциального поля 89
Глава 5. Оператор Гамильтона. Дифференциальные операции второго порядка. Оператор Лапласа 94
§ 20. Оператор Гамильтона «набла» 94
§ 21. Дифференциальные операции второго порядка. Оператор Лапласа 98
§ 22. Векторный потенциал 107
Глава 6. Криволинейные координаты. Основные операции векторного анализа в криволинейных координатах . 112
§ 23. Криволинейные координаты 112
1°. Цилиндрические координаты 113
2°. Сферические координаты 113
§ 24. Основные операции векторного анализа в криволинейных координатах 115
1°. Дифференциальные уравнения векторных линий . 113
2°. Градиент R ортогональных координатах 116
3°. Ротор в ортогональных координатах 117
4°. Дивергенция в ортогональных координатах 117
5°. Вычисление потока в криволинейных координатах . — 119
6. Нахождение потенциала в криволинейных координатах 120
7е. Вычисление линейного интеграла и циркуляции вектор ого поля в криволинейных координатах 123
§ 25. Оператор Лапласа в Ортогональных координатах 129
Ответы 131
Приложение 1 . 136
Основные операции векторного анализа в ортогональных криволинейных координатах 136
Приложение 2 138
Элементы площадей координатных поверхностей 138

О том, как читать книги в форматах pdf , djvu — см. раздел » Программы; архиваторы; форматы pdf, djvu и др. «

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Переменные векторы. Вектор-функции и их дифференцирование

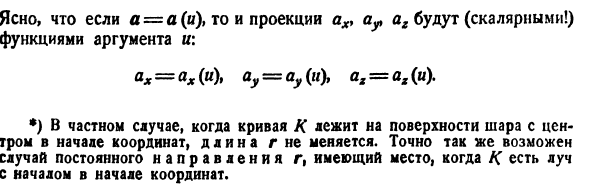
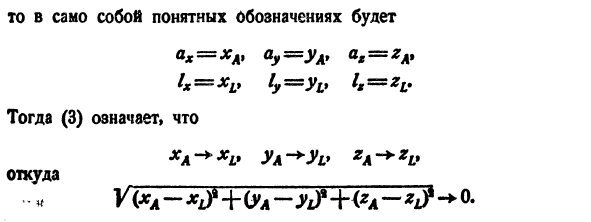
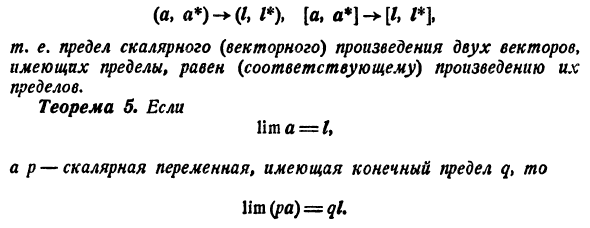
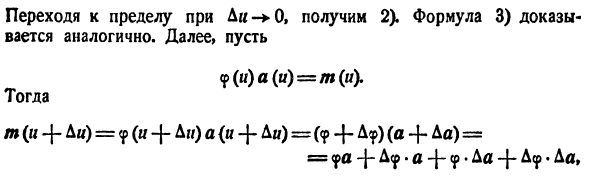
Видео:Годограф вектор функцииСкачать

Переменные векторы. Вектор-функции и их дифференцирование

• Переменный вектор. Векторные функции и их различие № 1. Переменный вектор. Функция вектора Годограф. Представьте себе точку M (x, y, z) t, движущуюся в пространстве вдоль определенной кривой K (рис. 293). Выберите единицу времени и первый момент. И любой момент времени характеризуется числом т.

Непрерывность векторной функции. Их дифференциация № 3. Непрерывность векторной функции. Различать их. Дай мне а = а (и) Функция вектора и скалярного аргумента. Как и в случае обыкновенных дифференциальных вычислений, если бесконечно малое приращение аргумента соответствует бесконечно малому приращению функции, a (n) называется непрерывным. lirn [a (u + Lee) -a (//)] = 0. (7) к- * 0 Равенство (7) также может быть описано в следующем формате: lim a (u — — di) = a (u). Где u0, a, — <Aw по n заменяет определение непрерывности. lim a (n) = a (a0). a- + io

Поэтому гл. II, свойство непрерывности вектор-функции означает, что предел (и u0) этой функции равен значению из предела аргумента. Далее поясняется операция дифференцирования непрерывной вектор-функции. Дай мне а = а (и) -Такую функцию. Давайте сделаем пять вещей: 1) Исправьте значение аргумента и найдите соответствующее значение функции a (s). 2) Дайте аргументу приращение A и найдите новое значение функции a (u — <- Au); 3) Найдите приращение Da = a (u + A «)

a (u). .v да (s + Dy) -a (s) 4) Настройте отношение -m— = —1-! -r1, -;

б) (s) и обозначается одним из символов. , T, h da a, a ‘(s), g. Нахождение ‘(u) называется производной функции a (u). *) Конечно, этого может и не быть.

Поверните A на ноль и ищите пределы *) lim * Джим Ли 0 Ли Аа 0 Ли Это ограничение называется производной функции a Людмила Фирмаль

Легко найти геометрический смысл производной a ‘(u). Для этого представим годограф векторной функции. Если (см. Рисунок 295) a (u) -OM, a (n-dY) = ON, тогда A a = LSH Отношение-вектор в том же направлении А Ды]> 0 для ММ, Di 0 и о = МП, Вы можете видеть, что вектор MP направлен на годограф по секущей линии.

Если Да -О (из-за непрерывности вектор-функции), точка N стремится соответствовать точке М. Поэтому предельное положение вектора MP направлено на годограф по касательной MQ. Однако эта предельная позиция n является производной от o ‘(u). Следовательно, производная вектор-функции направлена ​​по касательной к годографу этой функции. Пример. Переместить точку М в пространстве, r = r (t)

Векторное уравнение для этого движения. Годограф радиус-вектора r (0 — траектория точки М. Производная / (t) называется скоростью точки М. Следовательно, скорость точки — это вектор, который касается траектории этой точки. Этот вектор является направлением движения. И характеризуем скорость: r ‘(0 — предел длины вектора г (/ + ac-g (0 ат Учитывая ясность,Однако (рис. 296) DO-g (01 — длина кода MN, Включает в себя минимальную дугу MN точечной траектории. Как вы знаете, эти коды и дуги эквивалентны друг другу Поэтому друзья if’wi-lim, x, 1 w / a rW / r (t + AtJ

• Другими словами, длина вектора скорости является пределом отношения пути, по которому течет ток через бесконечно короткие промежутки времени. 296.Время этого периода Gap. Это скалярное значение — скорость точки. Направление вектора / (t) указывает направление движения. № 4. Формулы и правила дифференцирования векторных функций. Правила дифференцирования векторных функций полностью аналогичны правилам обыкновенных дифференциальных вычислений.

Они использованы в следующей таблице. a = a (u), b = b (u) -: векторная функция скалярного аргумента и вектор c-константы? (O) -скалярная функция и k-константа, v-скалярный аргумент, связанный с выражением q = u (m>): 1) ду * 6) рфа-дурь 2) d (a — — b) du da | du 1 db du * 7) rfu и i

. -A * + e du db du ‘8) rf (ffl) du 4) dfoa) du rfa. du * 9) d [ab] du б) д (ка) __ ду ■ к да • * ду ’10) да дв ‘да ду ду дв’ Формула 1) понятна. Положите s-a — — b, чтобы доказать 2). Тогда s + bs = (a — — Да) + отсюда D $ = Да + Db и AL, AB Я Ли 1 Ли

Когда вы достигнете предела Di 0, вы получите 2). Формула 3) тоже доказана. Дальше давайте

0, *) получается уравнение 4). Формулы 5) и 6) являются частными случаями 4). Уравнение 7) доказывается так же, как 4). Частные случаи 8) -7) и 9) такие же, как 4). Наконец, 10) доказывается точно так же, как и скалярный анализ.

Пусть ax, ay> ar — проекция вектор-функции a = a (n). тогда a = axi — — ay] — — атака. Используя уравнения 2) и 6) da_dax. , День da2- «Du

du J ^ Ifa Da Da Однако, когда вектор разлагается на векторы единичных координат, коэффициент единичного вектора i является проекцией разрешимого вектора на ось * Ox. так дакс н да du — iip * du 9

То есть проекция векторной производной на ось равна производной этой проекции на эту ось. Людмила Фирмаль

Пример. r = r (0 — радиус-вектор движущейся точки) М (х, у, z). Введите u =. Как вы уже знаете, v это скорость Точка М. Как сказано, vx = ^

-t. Но Tx = х. о Следовательно, проекция векторов на другие оси одинакова. Вот так дз дт *

То есть спроецированная скорость движущейся точки (на оси координат) равна производной соответствующей координаты по времени. Например, если точка движется как x = 8t * -1, = = z = tz + 1, vx = 16 /, r> y = 4, vz = 3Отс Выше называется «скорость движения®» и равна г / — = Y * 2LY * — — 1 () -) — 9/4 В момент времени t = 1, y = 16,8. *) Поскольку предполагается, что функция a (s) непрерывна, litnAa = 6 для Ли 0.

Равен длине временного интервала, отделяющего этот момент от первого момента. В этом случае знак присваивается номеру t. Или это зависит от того, следует ли момент интереса или предшествует первому моменту. Радиус-вектор r = OM в каждый конкретный момент t имеет определенную длину и направление. Однако их длина и направление со временем изменятся *). Итак, здесь мы имеем дело с переменными векторами. Как правило, переменные векторы — это векторы, которые различаются по длине или направлению.

Однако мы рассматриваем постоянные векторы как частный случай переменных (аналогично использованию констант в скалярном анализе). Скалярный анализ различал индивидуальные постоянные значения при работе с переменными. Фактически, переменная задача состояла из задачи этого набора значений. Аналогичным образом определим переменную вектор а Вы определите набор постоянных векторов — индивидуальное значение. В процессе изменения a принимает одно из этих значений. Если a является переменным вектором, его проекция ayt ax также является (скалярной!) Переменной. Установка вектора a эквивалентна установке переменных ay и av.

Если a принимает одно из своих значений, ay ay1 также принимает соответствующее постоянное значение. Очень важным примером переменного вектора является скалярная функция-вектор аргумента. Они говорят, что переменная vector a является векторной функцией скалярных аргументов, и каждое значение связано с определенным значением a. В этом случае они пишут а = а (к). г » И м Рисунок 293.

Если a = a (u), проекционный топор и ar ag являются (скалярными!) Аргументными функциями, ax = ax (u), y = a y (u), ax = ax (u). *) Длина r не изменяется, если кривая K находится на поверхности шара с центром в начале координат. Точно так же, если K — луч, происхождение которого является источником, это может быть в определенном направлении r.

Пример вектор-функции показан для радиус-вектора r = OM в точке M перемещения, описанной выше. Здесь, поскольку аргумент — время U, g = g (0- (1) Это уравнение называется векторным уравнением движения для точки М. Поскольку координаты точки M (x, y, r) являются проекциями ее радиус-вектора r, уравнение (1) можно заменить тремя скалярными уравнениями движения. x = x (t), y = y (f), z = z (t). Например, равенство x = Py y = 7t + 2, z = s nt Движение точки происходит. Их можно заменить одним векторным уравнением r = t4 — — (7t-2) / + sin tk.

Годограф определенного вектора переменных — это геометрическое положение конечных точек всех значений, если каждое значение откладывается от общей начальной точки. Годограф вектор-функции a (u) представляет собой (как правило, пространственную) кривую. Если все значения a (u) установлены на что-то отличное от источника, уравнение x = ax (u), y = ay (u), z = az (u) Представляет параметрическое уравнение вышеуказанной линии. Если вектор a (u) постоянен, годограф — это линия на поверхности шара.

Постоянный векторный годограф — это точка. Годограф радиус-вектора r = OM движущейся точки M является ее точкой. n ° 2. Векторное ограничение. Рассмотрим переменный вектор a, который изменяется в соответствии с законом *).Определение 1. Переменный вектор a называется бесконечно малым, если он имеет тенденцию быть нулевым по длине. Определение 2. Постоянный вектор I называется пределом переменного вектора a.

Разница между ними — бесконечно малый вектор. •) Например, a является векторной функцией скалярного аргумента a = a (s) и имеет определенные ограничения. Или, в более простом случае, пронумерованная последовательность постоянных значений alt at) atl …

Запишите с любой формулой Лима = /, а- + Л (Рис. 294) Приведите векторы / и a к общему началу координат 0 и приведите их в соответствие с началом координат. Далее разность I-a представлена ​​вектором AL. Если длина этого вектора стремится к нулю, точка A стремится соответствовать точке L, поэтому X A XV Однако, в конце концов (поскольку 0 соответствует началу координат), xA и xL являются проекциями векторов a и / на ось Ox. Таким образом, предыдущие отношения Я, — * / *.

Эта ситуация аналогична проекции векторов на другие оси. 80М это правда Рисунок 294. Теорема 1. Связь (2) (3) 1g lim a = 1 Это предполагает тройные отношения. 1G a9 Покажем, что обратное также верно в соответствии с теоремой 2. (3) — (2). Фактически, переместите векторы a и / к общему началу координат 0. Это совпадает с происхождением. В то же время конечными точками векторов a и I являются точки A и ξ. a = OAt 1 = O b

В понятной нотации * «= * # Ay = ul ‘*» = * # (3) чк

+ ги Откуда Y (XA- + (YA-Y0 * + (* A- * jf- * ° — и Последнее соотношение можно записать как AL — + 0, Это означает, что по определению 2 (2) верно. Таким образом, векторное соотношение (2) эквивалентно скалярному отношению тройка (3). Эта эквивалентность позволяет легко переносить наиболее важные свойства скалярных переменных в вектор.

Например, теорема 3I верна. а * л * т (4) тогда a + a * a-a * -> l-l * t (5) м. е. Предел суммы (разности) ограниченных векторов равен сумме пределов (разности). Конечно, это из (4) * * *! * ….. AJ-WJ. тогда i * -faj + ^ -f>> / j, -f l> 9 + + (6) Для простоты Если a — — a * = b, 1 + 1 * = m, (6) можно переписать в следующем формате bx-> tx% by —► tu, bg- * mt> По теореме 2 Lim 6 = / I Это эквивалентно первому соотношению (5). Второе доказывается аналогично. Подобные рассуждения доказывают еще две теоремы. Теорема 4. С (4)

(A, a *) — * (/, / *), [a, a *) -> — [/, / *], / я. д. Предел скалярного (векторного) произведения двух векторов с ограничениями равен (соответствующему) произведению этих ограничений. Теорема б. если И это = /, l p скалярная переменная с конечными ограничениями q> then lim (pa) = 0 /.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Мама, я Гейне! #26 Вектор-функцииСкачать

Оптимизация компоновки трехмерных геометрических объектов на основе годографа вектор-функции плотного размещения

Оптимизация компоновки трехмерных геометрических объектов на основе годографа вектор-функции плотного размещения

ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа

Видео:Геометрия 10 класс (Урок№18 - Компланарные векторы. Векторный метод решения задач.)Скачать

Введение

Обзор работ по проблеме упаковки/размещения трехмерных геометрических объектов (ГО), которая востребована во многих областях человеческой деятельности (компоновка [4], упаковка грузов, раскрой кристаллов и т. д.), позволяет сделать вывод, что сложность решения рассматриваемой задачи обуславливает отсутствие эффективных алгоритмов её решения. Большинство работ сводится к размещению простых геометрических фигур (параллелепипедов, цилиндров, сфер и т. д.). Поэтому поиск новых подходов и алгоритмов для решения задачи размещения трехмерных ГО остается актуальным.

Вычислительная сложность решения задачи трехмерной упаковки в общей постановке вынуждает вводить ряд упрощений, порой достаточно сильно сужающих область допустимых решений, однако позволяющих находить рациональные упаковки с приемлемыми затратами вычислительных ресурсов.

Одно из самых распространенных упрощений — фиксация ориентации ГО в пространстве или использование набора фиксированных ориентаций каждого из них.

В данной статье обсуждается задача размещения ориентированных произвольных невыпуклых многогранников сложных форм.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Постановка задачи

Задачу плотной упаковки ориентированных ГО в трехмерном пространстве можно свести к решению следующей математической задачи.

Имеется набор ориентированных трёхмерных ГО, каждый из которых имеет свою собственную систему координат.

Область упаковки , представляет собой прямоугольный параллелепипед

,

у которого — длина, — ширина объекта рассматриваются как константы, а — высота объекта , как переменная величина.

Введем следующие обозначения:

— смещение объекта на вектор ,

— граничные точки объекта ,

— внутренние точки объекта ,

— минимальная высота объекта для параметров размещения объектов множества .

Упаковкой назовем такой набор параметров размещения объектов , при котором выполняются следующие условия:

,
т. е. никакие два объекта не пересекаются между собой, и все объекты находятся внутри области размещения.

Требуется для ГО найти такую упаковку , чтобы высота области размещения была минимальной:

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Подходы к решению

Эту проблему можно рассматривать как задачу математического программирования [1], определенную на множестве допустимых размещений объектов в заданной области (т. е. размещений, удовлетворяющих ограничениям).

Одним из применяемых способов для решения таких задач является метод покоординатного спуска (метод Гаусса-Зайделя), который приводит к разбиению процесса решения на две части:

1. Моделирование плотного движения объектов в области размещения — внутренняя часть.

2. Формирование и изменение последовательности упаковываемых объектов — внешняя (комбинаторная часть).

Основной целью внутренней процедуры является обеспечение условий взаимного непересечения объектов. Для решения этой подзадачи рассмотрим подход, который базируется на понятии годографа функции плотного размещения ГФПР, разработанного и развитого до Ф-функций в харьковской школе академика [5], являющейся мировым научным лидером в этой области уже на протяжении многих десятилетий.

Под функцией плотного размещения двух соприкасающихся ГО понимается зависимость расстояния между некоторыми точками (полюсами) этих объектов от их взаимного плотного размещения (). Годограф вектора, направленного от одного полюса к другому, при плотном перемещении одного (подвижного) объекта вокруг другого (неподвижного) называется годографом функции плотного размещения (ГФПР). Таким образом, для упаковываемого объекта ГФПР представляет собой границу области, запрещенной для размещения этого объекта.

Видео:ВЕКТОРЫ решение задач 9 класс АтанасянСкачать

Описание особенностей применяемого метода решения

Пусть дан набор многогранников, каждый из которых имеет свою собственную систему координат и задается списками вершин и определяемых ими граней. Будем считать, что все точки каждого из объектов лежат в первом октанте, кроме того, каждый из них касается трех координатных плоскостей ().

В этом случае точка с минимальными координатами , принадлежащая его параллелепипедной оболочке, совпадает с началом координат.

1. Моделирование плотного движения объектов в области размещения.

Для обеспечения условий взаимного непересечения объектов между собой и с границей области размещения, требуется построить ГФПР Gij всех пар многогранников и для каждого многогранника построить ГФПР GQi к внешности области зоны размещения (хотя в этом случае эта область является невыпуклой, но ГФПР для нее строится тривиально).

Если рассматривать множество допустимых для размещения объекта точек, то оно представляет собой объединение областей, ограниченных различными ГФПР (в общем случае оно может быть несвязным). Точки локальных экстремумов будут являться вершинами вогнутостей, лежащими на границах этого объединения. Если один из пары объектов невыпуклый, то ГФПР будет также невыпуклым. Значит вершины невыпуклых ГФПР, образующие вогнутости, также являются точками локальных экстремумов. Следовательно, точка занесения при упаковке трехмерных невыпуклых многогранников может быть найдена в результате рассмотрения следующих случаев (для простоты описания будем считать, что номера объектов соответствуют позициям в приоритетном списке):

1. Вершина с минимальными координатами по Oz, Oy и Ox ГФПР размещаемого многогранника к области размещения — GQi. (Это соответствует следующему расположению: размещаемый многогранник касается трех граней области размещения.)

2. Вершина, являющаяся точкой пересечения ребер ГФПР размещаемого многогранника к области размещения — GQi и любых ГФПР размещаемого многогранника к уже размещенным многогранникам — . (Размещаемый многогранник касается одного из уже размещенных многогранников и двух смежных граней области размещения.)

3. Вершина, являющаяся точкой пересечения граней двух различных ГФПР размещаемого многогранника к размещенным многогранникам — и грани ГФПР размещаемого многогранника к области размещения — GQi. (Размещаемый многогранник касается двух других уже размещенных многогранников и грани области размещения.)

4. Вершина, являющаяся точкой пересечения граней трех различных ГФПР размещаемого многогранника к размещенным многогранникам — . (Размещаемый многогранник касается трех других уже размещенных многогранников.)

5. Вершина вогнутости ГФПР размещаемого многогранника к любому размещенному многограннику — . (Размещаемый многогранник касается трех граней уже размещенного многогранника.)

В процессе размещения очередного многогранника, проанализировав все 5 случаев соприкосновений, получаем набор точек, каждая из которых является точкой локального экстремума. В целях минимизации высоты контейнера из всего полученного множества выбирается точка с минимальной координатой по z, в случае совпадения z – с минимальной суммой координат x и y.

Для большей наглядности на рис.1 представлены примеры двумерных аналогов описанных случаев.

На рисунке тонкими линиями показаны границы объектов, жирными – ГФПР, тонкими пунктирными – границы размещаемого объекта при размещении в точке локального минимума, жирными пунктирными – границы объекта при его размещении в соответствии с глобальным минимумом. Жирными точками показаны полюса объектов. Квадратами помечены точки локального минимума не имеющие минимальной координаты по Oz.

Рассмотрим размещение четырех объектов по шагам, при этом на каждом шаге будем размещать объект с соответствующим номером:

Шаг 1: Точка локального минимума принадлежит вершине ГФПР объекта T1 к зоне размещения Q — GQ1. Зафиксируем полюс объекта T1 в этой точке (Рис.1а).

Шаг 2: Найдено 2 точки локального минимума:

— одна из которых принадлежит вершине ГФПР объекта T2 к упакованному объекту T1 – G12;

— одна — точка пересечения ГФПР объекта T2 к области размещения Q — GQ2 и ГФПР объекта T2 к упакованному объекту T1 — G12.

Зафиксируем многоугольник T2 в точке с минимальной координатой по Oz и затем по Ox – это нижняя точка пересечения GQ2 и G12 (Рис.1б).

Шаг 3: Найдено 2 точки локального минимума:

— одна из которых является точкой пересечения ГФПР объекта T3 к упакованным объектам T1 и T2 — G13 и G23;

— одна — точка пересечения ГФПР объекта T3 к области размещения Q — GQ3 и ГФПР объекта T3 к упакованному объекту T2 — G23.

Зафиксируем многоугольник T3 в точке с минимальной координатой по Oz и затем по Ox – это точка пересечения G13 и G23 (Рис.1в).

Шаг 4: Точка локального минимума принадлежит вершине ГФПР объекта T4 к упакованному объекту T1 – G14. Зафиксируем полюс объекта T4 в этой точке (Рис.1г).

При реализации данного подхода возникают задачи нахождения точки пересечения отрезка и многогранника, отрезка и грани, двух многогранников. Все они подробно рассмотрены в работе [2]. Для поиска ГФПР двух многогранников используется алгоритм, описанный в статье [3].

Рис.1. Размещение четырех объектов T1, T2, T3 и T4 в области Q:

а) годограф GQ1 объекта T1 и области размещения Q, точка занесения, соответствующая точке локального минимума (размещение первого объекта T1 в пустой области Q);

б) годограф GQ2 объекта T2 и области размещения Q, годограф G12 объекта T2 и объекта T1, точка занесения (размещение второго объекта T2 в области Q с размещенным объектом T1);

в) годограф GQ3 объекта T3 и области размещения Q, годографы G13 и G23 объекта T3 и объектов T1 и T2, точка занесения (размещение третьего объекта T3 в области Q с размещенными объектами T1 и T2).

г) годограф GQ4 объекта T4 и области размещения Q, годографы G14, G24 и G34 объекта T4 и объектов T1, T2 и T3, точка занесения (размещение четвертого объекта T4 в области Q с размещенными объектами T1, T2 и T3).

2. Формирование и изменение последовательности упаковываемых объектов

В рассматриваемом подходе для формирования упаковок многогранников были реализованы следующие способы организации внешней процедуры оптимизации:

1)первый подходящий с упорядочиванием ППсУ (Рис.2.) объектов в порядке убывания объемов (простая схема), а также его улучшение – локальный поиск (циклическая схема);

Рис.2. Блок-схема, описывающая алгоритм ППсУ.

2)«жадный» метод с выбором на каждом шаге того объекта, который укладывается лучше других (совмещенная схема);

3)GRASP (Greedy Randomized Adaptive Search Procedures – Жадные Рандомизированные Адаптивные Процедуры Поиска) является итеративным методом, при каждом запуске которого выполняются две процедуры:

— генерация начального решения;

При каждой генерации могут быть использованы различные значения параметра случайности α. Этот параметр используется в критерии проверки возможности выбора объекта для размещения:

. (1)
– высота размещения объекта .

– минимальная высота размещения по всем объектам.

– максимальная высота размещения по всем объектам.

При α = 0 неравенство (1) преобразуется к виду , тогда любой объект может быть выбран для размещения – «случайная» конструкция. При α = 1 неравенство (1) преобразуется к виду , тогда может быть выбран объект , у которого – «жадная» конструкция. При любом значении α выбирается случайный объект из множества объектов удовлетворяющих неравенству (1).

Очевидно, что функция зависимости качества размещения от значения параметра α нелинейная. Поэтому генерацию начального решения следует производить со значениями α из диапазона [0, 1] с некоторым шагом Δα, начиная с 0.

Локальный поиск используется для поиска локального оптимума в окрестности каждого из сгенерированных решений, а затем дополнительно применяется к лучшему найденному.

GRASP является комбинацией совмещенной и циклической схем.

Рис.3. Блок-схема, описывающая алгоритм GRASP.

Рис.4. Блок-схема, описывающая процедуру генерации начального решения GRASP.

При реализации локального поиска для нахождения окрестного решения использована следующий подход: выбирается объект, упаковка которого привела к самому большому увеличению высоты зоны размещения, и меняется порядковыми номерами с любым другим объектом.

1. Определение точки размещения многогранника

L, W – длина и ширина основания зоны размещения;

T – список всех многогранников;

j – индекс размещаемого объекта;

step – количество размещенных многогранников;

– точки занесения размещенных многогранников.

u – координаты точки занесения.

1. Проверка на касание трех граней зоны размещения.

2. Проверка на касание трех граней одного из уже упакованных многогранников.

ДЛЯ i ОТ 1 ДО step ДЕЛАТЬ

В процессе последовательного нахождения каждой точки utest вогнутости ГФПР GPP(Ti, Tj):

3. Проверка на касание двух граней зоны размещения и одной грани уже упакованного многогранника.

В процессе последовательного нахождения каждой точки utest пересечения граней ГФПР GPP(Ti, Tj) и ребер GQP(Tj):

4. Проверка на касание грани зоны размещения и двух граней уже упакованных многогранников.

В процессе последовательного нахождения каждой точки utest пересечения граней ГФПР GQP(Tj) и отрезков E:

5. Проверка на касание трех граней различных уже упакованных многогранников.

В процессе последовательного нахождения каждой точки utest пересечения граней ГФПР GPP(Tl, Tj) и отрезков E:

u – лучший найденный параметр размещения;

utest – проверяемый параметр размещения.

ЕСЛИ utest ≥ u ТО ВОЗВРАТ u КОНЕЦ ЕСЛИ

ДЛЯ i ОТ 0 ДО step ДЕЛАТЬ

2. Формирование и изменение последовательности упаковываемых объектов

– многогранники.

L, W – длина и ширина основания зоны размещения.

l – количество запусков локального поиска.

– параметры размещения многогранников.

Найдем объемы многогранников

Выполним сортировку массива T в порядке уменьшения объемов <Vi>

ДЛЯ i ОТ 1 ДО n ДЕЛАТЬ

– многогранники.

L, W – длина и ширина основания зоны размещения.

l – количество запусков локального поиска.

Δα – шаг изменения параметра случайности α.

– параметры размещения многогранников.

ДЛЯ α ОТ 0 ДО 1 С ШАГОМ Δα ДЕЛАТЬ

ЕСЛИ ИЛИ un(z) > uαn(z) ТО

ДЛЯ i ОТ 1 ДО n ДЕЛАТЬ

– массив параметров размещения на i-том шаге

ДЛЯ j ОТ 1 ДО n ДЕЛАТЬ

Отсортируем точки массива Ui в порядке возрастания координаты (z).

ПроизвольныйЭлементИз()

ДЛЯ i ОТ 1 ДО l ДЕЛАТЬ

Найти

Сгенерировать случайное число

Создать последовательность Tlocal, которая отличается от Tcur перестановкой элементов с номерами max и any

Если размещение в соответствии с порядком Tlocal было рассмотрено ранее, то повторим генерацию any, иначе продолжим

Разместим многогранники Tlocal в соответствии с найденным порядком

💡 Видео

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Метод годографа и центростремительное ускорениеСкачать

8 класс, 48 урок, Применение векторов к решению задачСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Урок 11. Решение задач на действия с векторамиСкачать

100 тренировочных задач #135 Угол между векторамиСкачать

Скалярное произведение векторов. 9 класс.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Урок 9. Проекции вектора на координатные осиСкачать