Четырехугольник есть центр симметрии (6 видео)

Как доказать, что фигура – параллелограмм? Какие его признаки?

Содержание

Содержание:
Что такое параллелограмм, свойства фигуры
Как доказать, что фигура параллелограмм
Признаки
Признаки параллелограмма по диагоналям с доказательством
Прочие способы как доказать параллелограмм
Докажите, что если четырёхугольник имеет центр симметрии, то этот четырёхугольник — параллелограмм.
Ваш ответ
Похожие вопросы
Осевая и центральная симметрии
🎥 Видео

Содержание:

Параллелограммом – 4-угольник, где противоположные стороны попарно параллельные, одинаковые по длине, а диагонали в точке пересечения делятся на равные отрезки. Изучим признаки параллелограмма по двум, четырём сторонам, внутренним углам, центру симметрии.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Что такое параллелограмм, свойства фигуры

Особенность высоты геометрической фигуры – отрезка, опущенного из любой точки многоугольника на противоположную ей сторону: отсекает от фигуры равнобедренный треугольник.

Свойства биссектрис – отрезков, делящих углы пополам:

биссектрисы пересекаются под углом 90°;
равноделящие, лежащие одна напротив другой относительно центра симметрии углов, параллельные и равные по длине.

У 4-угольника противоположные углы равны, а сумма прилегающих к одному отрезку составляет 180°.

Видео:Осевая симметрия. 6 класс.Скачать

Как доказать, что фигура параллелограмм

Признаки

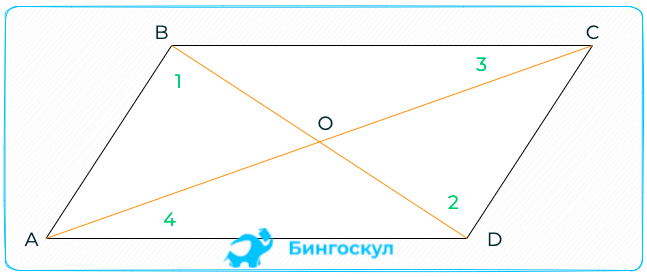
Дан 4-угольник, где AB=CD, BC=AD. Доказать, что AB∥CD, BC∥AD.

Проведём диагональ BD. В итоге получим пару одинаковых треугольников, исходя из условий задачи и общего отрезка BD.

Отсюда вытекают равенства: ∠1 = ∠4, ∠2 = ∠3 – подобные треугольники имеют одинаковые по величине углы, образованные подобными сторонами. Значит AB∥CD и BC∥AD (из свойства: если накрест расположенные углы равны, значит прямые будут параллельными).

Второй признак – 4-угольник с равными по длине и параллельными противоположными сторонами относится к параллелограмму.

В данном четырёхугольнике BC=AD, BC∥AD. Нужно доказать параллельность AB и CD для подтверждения, что это параллелограмм.

Исходя из условий, понимаем, что BCD и ABD – подобные треугольники. Из условия задачи: BC = AD, BD – общая для обоих, значит, ∠2 = ∠3 – следствие того, что накрест лежащие углы подобные. Из равенства 3-угольников: ∠1 = ∠4 получается, что AB параллельна CD.

Видео:Ось симметрииСкачать

Признаки параллелограмма по диагоналям с доказательством

Четырёхугольник обладает и прочими особенностями, рассмотрим одну на примере задачи: докажите признак параллелограмма по точке пересечения диагоналей.

Треугольник AOD равен BOC, потому что AD=BC – лежащие напротив стороны четырёхугольника. ∠1=∠2, ∠3=∠4 – они лежат накрест и параллельных прямых. Если треугольники подобные, значит: OC=OA, OB=OD.

Прочие способы как доказать параллелограмм

Получается, треугольник OAF равен OCE, потому что у них стороны AO = OC. Углы, расположенные у общей вершины O, также равны, ведь они вертикальные. ∠1=∠2 – следствие равности накрест лежащих при параллельных прямых углов. Как результат: OF=OE.

Если у четырёхугольника есть точка, которая обладает описанным свойством, её называют центром симметрии этой геометрической фигуры. Для рассматриваемого многоугольника центром симметрии является точка O, разделяющая диагонали на подобные отрезки.

При повороте геометрической фигуры вокруг центра симметрии на 180° она будет совмещена с предыдущим местоположением, ведь противоположные точки поменяются местами относительно оси симметрии.

Для проверки качества усвоения материала самостоятельно сформулируйте признаки параллелограмма без доказательств.

Видео:Осевая и центральная симметрия, 6 классСкачать

Докажите, что если четырёхугольник имеет центр симметрии, то этот четырёхугольник — параллелограмм.

Видео:Осевая и центральная симметрия.Скачать

Ваш ответ

Видео:Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать

Осевая и центральная симметрии

Если прямая проходит через середину отрезка А₁А₂ и перпендикулярна к нему, то точки А₁ и А₂ называются симметричными относительно прямой . Каждая точка прямой симметрична самой себе.

Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре. Прямая — ось симметрии фигуры.

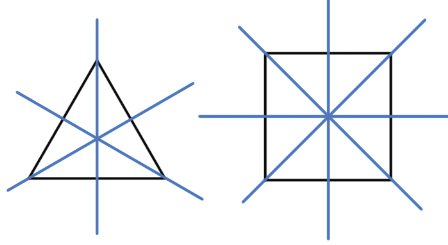
Пример (синим цветом обозначены оси симметрии):

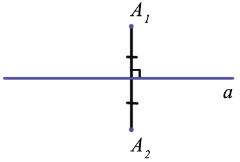
Точки А₁ и А₂ называются симметричными относительно точки О, если О — середина отрезка А₁А₂. Точка О считается симметричной самой себе.

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры.

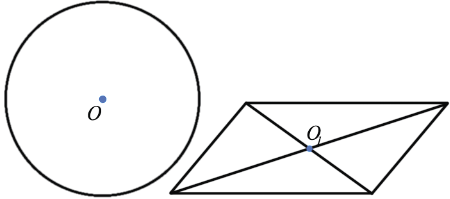
Пример (синим цветом обозначены центры симметрии):