Четырёхугольник ABCD вписан в окружность радиуса R = 10. Известно, что AB = BC = CD = 6.
а) Докажите,что прямые BC и AD параллельны.
а) Острые углы BCA и CAD равны, поскольку опираются на дуги стянутые равными хордами AB и CD. Значит, прямые BC и AD параллельны.
б) Обозначим угол BCA через α. По теореме синусов для треугольника ABC имеем
Треугольник ABC равнобедренный, поэтому Значит,
Четырехугольник ABCD — равнобедренная трапеция, поэтому
Значит,
По теореме синусов для треугольников ACD и ACB получаем: откуда, используя формулу синуса тройного угла, получаем:
Приведем другое решение пункта б)
Заметим, что центр описанной окружности лежит вне трапеции. Проведем две высоту трапеции BH — из вершины B и параллельную ей прямую EF проходящую через центр окружности. Обозначим AE = x, OE = y. Тогда из треугольника AOE по теореме Пифагора имеем а из треугольника BOF:
Тогда высота трапеции
а AH = x – 3. Напишем теорему Пифагора для треугольника ABH:
Подставим полученный результат в первое уравнение и решим его.
Очевидно, что нам подходит только положительный корень, откуда AD = 2x = 15,84.
Приведем решение пункта б), присланное читателем сайта.
Так как AB = BC = CD, эти хорды стягивают равные дуги. Значит,
По теореме синусов для треугольника ABC имеем:
откуда
Опустим высоту BH на основание AD. Тогда
Ответ: б)
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:Геометрия Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB = BC = CD = 12Скачать  Четырехугольник авсд вписан в окружность радиуса 10 известно что ав вс сдЧетырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB = BC = CD = 12. а) Докажите, что прямые BC и AD параллельны. а) Рассмотрим ∆АВС: ∠BAC=∠BCA (так как AB = BC) Пусть ∠BAC = ∠ BCA = x˚ ∠BCA = ∠BDA = x˚ (так как вписанные углы, опирающиеся на одну и ту же дугу, равны) Аналогично ∠BAC = ∠BDC = x˚ ∠BDC = DBC = x˚ (так как BC = DC) ∠DBC = ∠DAC = x˚ (так как вписанные углы, опирающиеся на одну и ту же дугу, равны) Получаем, что ∠CAD = ∠BCA = x˚. Отсюда следует, что BC || AD при секущей AC. б) Рассмотрим ∆ABC и воспользуемся теоремой синусов: Для того, чтобы найти сторону AD, воспользуемся теоремой синусов для ∆ADC: Найдем sin3x = sin(x+2x) = sinxcos2x + sin2xcosx = sinxcos2x + 2sinxcos 2 x = sinx(cos2x + 2cos 2 x) = sinx(2сos 2 x — 1 + 2cos 2 x) = sinx(4cos 2 x — 1) = sinx(4(1-sin 2 x) — 1) = sinx(3-4sin 2 x) = 3sinx — 4sin 3 x = 3⋅3/4 — 4⋅(3/4) 3 = 9/4 — 27/16 = 36/16 — 27/16 = 9/16 Подставляем найденное значение sin3x в выражение AD/sin3x = 2R: Ответ: б) 9 Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Решение задачи №16 с настоящего ЕГЭ 2018Условие задачи Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB=BC=CD=12. а) Докажите,что прямые BC и AD параллельны. Решение а) Докажем, что BC∥AD. Равные дуги стягиваются равными хордами. Дуги АВ и CD, стягиваемые равными хордами АВ и CD, равны. Значит, ∠АСВ=∠CAD — как опирающиеся на равные дуги. Эти углы — накрестлежащие при прямых BC и AD и секущей АС. б) Найдем AD, если АВ=ВС=CD=12, R=8. — так как опираются на равные хорды. Так как ABCD — равнобедренная трапеция, По теореме синусов из треугольника CDA: По теореме косинусов из △ACD: ‘ alt=’sin varphi =displaystyle frac = >’ /> x=12 или х =9. 📸 ВидеоЧетырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Четырехугольник АВСD со сторонами АВ=12 иСD=13 вписан в окружность. 27 вариант Ященко ОГЭ задача 25Скачать  Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Четырехугольники, вписанные в окружность. 9 класс.Скачать  Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать  Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать  2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать  #29. Регион ВсОШ 2023, 9.5Скачать 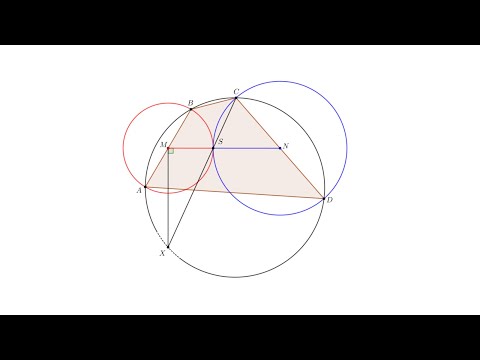 Четырёхугольник ABCD вписан в окружность причём BC CD Известно что угол ADC равен 93Скачать  Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать  Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать  2122 в четырёхугольник ABCD вписана окружность AB равно 17 CD равно 22Скачать  Геометрия Сторона AD четырехугольника ABCD является диаметром окружности, описанной около негоСкачать  ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать  Задача 6 №27876 ЕГЭ по математике. Урок 117Скачать  На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Задача 6 №27874 ЕГЭ по математике. Урок 115Скачать  Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать  |



