Четырехугольник abcd описан около окружности с центром о найдите сумму углов аов и cod

Школе NET

Register

Do you already have an account? Login

Login

Don’t you have an account yet? Register

Newsletter

Submit to our newsletter to receive exclusive stories delivered to you inbox!

• Главная 
• Вопросы & Ответы 
• Вопрос 6603231

Онтонио Веселко

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Четырёхугольник ABCD описан около окружности, с центром в точке О. Докажите, что сумма градусных мер углов: a)AOB и COD; 6)BOC и AOD равна 180°. Четырёхугольник ABCD описан около окружности, с центром в точке О. Докажите, что сумма градусных мер углов:
a)AOB и COD; 6)BOC и AOD равна 180°.

Видео:16) Четырехугольник АВСD описан около окружности, AD=7, DC=12, BC=13. Найдите AB. Математика огэ.Скачать

Геометрия: Планиметрия в тезисах и решениях. 9 класс (16 стр.)

114. В треугольнике ABC проведены высоты AD и СЕ. Докажите, что треугольники ABC и DBE подобны. Чему равен коэффициент подобия (рис. 184)? (2)

Решение. Из прямоугольного треугольника ВСЕ: BE = ВС ? cos В. Из ?ABD: BD = АВ ? cos В. Значит, две стороны BD и BE треугольника BDE пропорциональны сторонам АВ и ВС треугольника ABC, а угол В (угол между пропорциональными сторонами) у треугольников общий. ?BDE

?ABC по двум сторонам и углу между ними.

Ответ: kподобия = cos B.

115. В равносторонний треугольник вписана окружность. Этой окружности и сторон треугольника касаются три малые окружности. Найдите сторону треугольника, если радиус малой окружности равен 1 (рис. 185). (2)

Решение. Так как в равностороннем треугольнике ABC угол ABC = 60°, то ?ОВМ = 30° (см. рис.). Из центров О и О1 проведем перпендикуляры ОМ и О1Т к стороне ВС. По условию О1Т и О1K равны 1. Длины отрезков ОМ и ОК обозначим через R. Из треугольника ВТО1 следует, что ВО1 = О1Т/sin 30° = 1/0,5 = 2. Треугольники ВТО1 и ВМО подобны по двум углам (?BTO1 = ?BMO = 90°; ?OBM – общий). Отсюда следует, что O1T/O1B = OM/OB;

Теперь мы знаем радиус вписанной в равносторонний треугольник окружности. Осталось найти длину его стороны. Из треугольника ВОМ следует ВМ = OM ? ctg ?ОВМ = 3?3. Тогда ВС = 2ВМ = 6?3.

116. Из одной точки к окружности проведены две касательные. Длина каждой касательной равна 12 см, а расстояние между точками касания 14,4 см. Определите радиус окружности (рис. 186). (2)

Решение. Пусть ОА и ОВ – касательные к окружности с центром С; А и В – точки касания. Тогда СВ ? ОВ, СА ? ОА. Кроме того, ОС ? АВ и делит эту сторону пополам. ОА = 12 см, AM = 1/2 АВ = 7,2 см.

?МОА = ?АОС (углы с взаимноперпендикулярными сторонами), значит, ?ОАС подобен ?ОАМ; тогда

117. Центр О окружности радиуса длиной 3 лежит на гипотенузе АС прямоугольного треугольника ABC. Катеты треугольника касаются окружности. Найти площадь треугольника ABC, если известно, что длина отрезка ОС равна 5 (рис. 187). (3)

Решение. Пусть ABC – данный в условии задачи треугольник. Обозначим через M и N точки касания окружности соответственно со сторонами АВ и ВС. Соединив эти точки с центром О окружности, получим квадрат MBNO, и поэтому BN = ОМ = 3. Треугольник ONC прямоугольный, в нём ОС = 5, ON = 3. Следовательно,

Но тогда ВС = NC + NB = 7. Треугольники ONC и ABC подобны, поэтому AB/ON = BC/NC; AB/3 = 7/4; отсюда получаем, что AB = (ON ? BC)/NC = (3 ? 7)/4 = 21/4. Теперь находим S – площадь прямоугольного треугольника ABC:

Задачи для самостоятельного решения

118. В равнобедренный треугольник вписан параллелограмм так, что угол параллелограмма совпадает с углом при вершине треугольника, а вершина противолежащего угла лежит на основании. Докажите, что периметр параллелограмма есть величина постоянная для данного треугольника. (1)

119. Из точки D, лежащей на катете АС прямоугольного треугольника ABC, на гипотенузу СВ опущен перпендикуляр DE. Найдите длину CD, если СВ = 15, АВ = 9, СЕ = 4. (1)

120. Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40 см. Найдите катеты треугольника. (1)

121. В параллелограмме ABCD проведена диагональ BD и отрезок AF (F ? ВС), пересекающий BD в точке О. Известно, что ВО = 6, OD = 18, FB = 4. Определите сторону параллелограмма AD. (1)

122. В острый угол, равный 60°, вписаны две окружности, извне касающиеся друг друга. Радиус меньшей окружности равен 1. Найдите радиус большей окружности. (1)

123. Найдите длину стороны квадрата, вписанного в равнобедренный треугольник с основанием а и боковой стороной b так, что две его вершины лежат на основании, а две другие вершины – на боковых сторонах. (2)

124. В параллелограмме ABCD точка М– середина стороны СВ, N – середина стороны CD. Докажите, что прямые AM и AN делят диагональ BD на три равные части. (2)

125. В трапеции, основания которой равны а и b, через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найдите длину отрезка этой прямой, отсекаемого боковыми сторонами трапеции. (2)

126. В остроугольном треугольнике ABC из вершин А и С на стороны ВС и АВ опущены высоты АР и CQ. Известно, что площадь треугольника ABC равна 18, площадь треугольника BPQ равна 2, а длина отрезка PQ равна 2?2. Вычислите радиус окружности, описанной около треугольника ABC. (3)

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

2.6. Задачи на вписанные и описанные четырёхугольники

Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны.

Если около четырёхугольника можно описать окружность, то суммы противоположных углов равны 180°.

Примеры решения задач

127. Известно, что в трапецию ABCD с основаниями AD и ВС можно вписать окружность и около неё можно описать окружность, EF – её средняя линия. Известно, что АВ + CD + EF = 18. Найдите периметр трапеции (рис. 188). (1)

Решение. Так как в трапецию можно вписать окружность, то

Поскольку около трапеции можно описать окружность, то АВ = CD. Пусть АВ = CD = а; тогда из (1) следует AD + ВС = 2а и

По условию АВ + CD + EF = 18; тогда с учетом (2) получаем: а + а + а = 18; а = 6. Периметр трапеции PABCD = АВ + CD + AD + BC = 2(АВ + CD) = 4а = 24.

128. Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой стороной, равной 17 см. Найдите основания трапеции (рис. 189). (2)

Решение. Очевидно, что высота трапеции равна диаметру окружности. Высота ВК = 15 см; из прямоугольного треугольника АВК

Пусть BС = х, тогда AD = 8 + х + 8 = х + 16. Так как в трапецию вписана окружность, то AD + ВС = АВ + CD; х + 16 + х = 17 + 17; х = 9 см; AD = 9 + 16 = 25 см.

Ответ: 9 см; 25 см.

Задачи для самостоятельного решения

129. Четырёхугольник ABCD описан около окружности с центром О. Найдите сумму углов АОВ и COD. (1)

130. Определите площадь круга, вписанного в прямоугольную трапецию с основаниями а и b. (2)

131. Длины боковых сторон трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит её на две части, отношение площадей которых равно 5/11. Найдите длины оснований трапеции. (3)

Видео:В окружности с центром O AC и BD – диаметры ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

2.7. Задачи на вписанные углы

Вписанный в окружность угол равен половине центрального угла, опирающегося на ту же дугу.

Примеры решения задач

132. Найдите ?ТОК, если О – центр окружности и ?ТЕК = 120° (рис. 190).(1)

Решение. Так как вписанный угол ТЕК равен половине центрального угла, опирающегося на ту же дугу, то

133. Дан правильный 30-угольник А1А2 . А30 с центром О. Найдите угол между прямыми ОА3 и А1А4 (рис. 191). (2)

Решение. Так как многоугольник А1А2 . A30 – правильный, то ?А3ОА4 = 360°/30 = 12°. Далее, ?А3А1А4 = 1/2 ?А3ОА4 = 6° (вписанный угол, опирающийся на дугу А3А4). ?А1ОА3 = 2 ? 12° = 24°;

Требуемый нам угол х является внешним углом к треугольнику А3А1В. Так как внешний угол треугольника равен сумме внутренних углов, с ним не смежных, то х = 6° + 78° = 84°.

134. В окружность вписан четырёхугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке Е. Прямая, проходящая через точку Е и перпендикулярная к АВ, пересекает сторону CD в точке М. Доказать, что ЕМ – медиана треугольника CED, и найти её длину, если AD = 8 см, АВ = 4 см и ?CDB = ? (рис. 192). (3)

Решение. Обозначим через К точку пересечения прямых АВ и ЕМ. Поскольку углы CDB и CAB опираются на одну и ту же дугу ВС, то ?CAB = ?CDB = ?. Из равенств ?DCE + CDB = ?/2, ?КЕА + ?САВ = ?/2, следует, что ?DCE = ?КЕА = ?СЕМ. Но это означает, что треугольник СЕМ равнобедренный, т. е. СМ = ЕМ. Далее, ?MED = ?/2 – ?СЕМ = ?/2 – (?/2 – ?) = ?CDB.

Итак, треугольник EMD равнобедренный, или DM = ЕМ. Этим доказано, что СМ = DM или что ЕМ – медиана треугольника CED.

Из прямоугольного треугольника ABE находим

АЕ = АВ ? cos?ЕАВ = АВ ? cos?CAB = 4 ? cos ?.

Далее, из прямоугольного треугольника AED по теореме Пифагора получаем

Задачи для самостоятельного решения

135. Окружности с центрами О и О1 касаются внутренним образом. Найдите угол В (рис. 193). (1)

136. Точка находится внутри круга радиуса 6 и делит проходящую через неё хорду на отрезки длиной 5 и 4. Найдите расстояние от точки до окружности. (2)

137. а) Докажите, что

138. Диагональ BD четырёхугольника ABCD является диаметром окружности, описанной около этого четырёхугольника. Вычислить длину диагонали АС, если BD = 2, AB = 1, ?ABD:?DBC = 4:3. (3)

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Четырехугольник abcd описан около окружности с центром о найдите сумму углов аов и cod

Четырехугольник ABCD вписан в окружность с центром в точке О. Радиус АО перпендикулярен радиусу ОВ, а радиус ОС перпендикулярен радиусу OD.

а) Докажите, что ВС || AD.

б) Найдите площадь треугольника АОВ, если длина перпендикуляра, опущенного из точки С на AD, равна 9, а длина отрезка ВС в два раза меньше длины отрезка AD.

а) Поскольку треугольник BOC равнобедренный, а треугольники AOB и COD равны по первому признаку, то углы ABC и BCD равны. Аналогично равны углы BAD и ADC, и прямые параллельны.

б) Найдем радиус окружности. Пусть он равен R, BC = 2x, AD = 4x. Проведем в равнобедренной трапеции ABCD высоту CH = 9. Она разбивает основание AD на отрезки AH = 3x, DH = x. Заметим, что вписанный Значит, треугольник CHA — равнобедренный прямугольный, 3x = 9, x = 3. По теореме Пифагора получаем Тогда радиус окружности а

Ответ: б)

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, 📺 Видео Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать 🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать 2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать 🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать ЕГЭ 2023 математика Вариант 5 задача 1Скачать 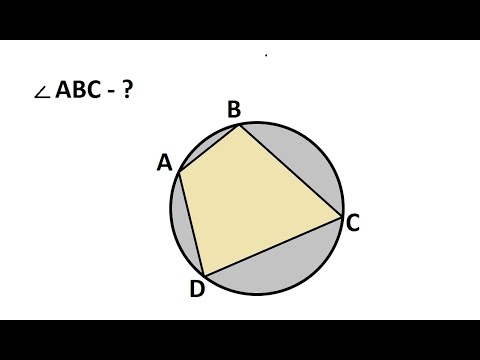№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать 2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать ЕГЭ 2022 16 вариант 3 задача.Скачать 11 класс, 44 урок, Описанный четырехугольникСкачать Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать Поделиться или сохранить к себе: Смотрите также Является ли четырехугольник прямоугольником если все его углы равны все его стороны равны Является ли четырехугольник параллелограммом если сумма его соседних углов равна 180 градусам Является ли четырехугольник параллелограммом если сумма его соседних углов равна 180 degree180 Является ли четырехугольник параллелограммом если его противоположные углы равны да или нет Чья комната походила как будто на сарай имела неправильный вид четырехугольника Что можно сказать о четырехугольнике если серединные перпендикуляры пересекаются в одной точке Четырехугольники авсд и дсеф имеют общую сторону сд точки а д ф Четырехугольник является правильным если все его стороны равны и один из углов