Эпюр треугольника как строить (3 видео) | Курс школьной геометрии

Методическое пособие «Эпюр № 1выполнено на основе учебного пособия

Содержание

Главная > Методическое пособие
Оглавление
ВВЕДЕНИЕ
ОБЩИЕ УКАЗАНИЯ
МЕТОДИКА РЕШЕНИЯ ЭПЮРА
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ ЭПЮРА
ПРИЛОЖЕНИЕ 1
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Московский государственный университет путей сообщения (МИИТ)
Построить натуральную величину треугольника авс
Метки
Натуральная величина треугольника с описанием.
Алгоритм определения натуральной величины плоскости:
Замена плоскостей проекции
Плоскопараллельное перемещение
🎬 Видео

Главная > Методическое пособие

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Видео:Задание: ЭпюрСкачать

ВВЕДЕНИЕ

Методическое пособие «Эпюр № 1выполнено на основе учебного пособия А. И. Образцова, изданного в 1953 году.

Данное пособие предназначено для оказания помощи студентам при выполнении графической работы «Эпюр №1» по курсу «Начертательная геометрия».

Цель работы — научиться строить линию пересечения заданных плоских фигур, определять видимость этих фигур на проекциях.

Графическая работа «Эпюр №1» является первым самостоятельным заданием студента по дисциплине «Начертательная геометрия». Для выполнения этой работы студент должен изучить следующие разделы начертательной геометрии: «Точка и прямая», «Плоскость», «Взаимное положение прямой и плоскости», «Взаимное положение двух плоскостей».

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

ОБЩИЕ УКАЗАНИЯ

Графическая работа «Эпюр №1» выполняется в масштабе 1:1 на формате А3 (297420 мм). В правом нижнем углу формата А3 студент выполняет основную надпись – форма 1 по ГОСТ 2.104-68. Пример заполнения основной надписи приведен в Приложении I. В левом верхнем углу формата выполняется дополнительная графа 26 (1470 мм). Пример выполнения графической работы дан в Приложении I.

В соответствии с ГОСТ 2.303-68 задание выполняется следующими типами линий:

— линии видимого контура толщиной S, равной 0,60,8 мм;

— линии построения – сплошные тонкие, толщиной от до ;

— линии невидимого контура – штриховые, толщиной от до ;

— следы вспомогательных плоскостей-посредников изображаются разомкнутыми линиями, длиной 8-10 мм, толщиной от 1,5 S до 2 S .

Видео:ЗАДАЧИ ПО ОСНОВАМ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ. МЕТОДЫ ПРОЕЦИРОВАНИЯ И ЭПЮРЫ ТОЧЕК. №1Скачать

МЕТОДИКА РЕШЕНИЯ ЭПЮРА

Вариант задания включает в себя три различные геометрические плоские фигуры:

— фигура № 1 задана координатами трех точек, фигура № 2 (многоугольник) полностью задана координатами трех точек и оставшимися точками, у которых одна из координат заменяется условием их принадлежности к плоской фигуре № 2;

— фигура № 3 занимает проецирующее положение (фронтально-проецирующее или горизонтально-проецирующее) и задается очерком в виде кольца, серпа, круга или его части.

Выполнение эпюра состоит из графического решения нескольких задач:

достроить недостающую проекцию многоугольника;

построить проекции линии пересечения треугольника АВС и многоугольника;

построить проекции линии пересечения: треугольника с плоскостью частного положения; многоугольника с плоскостью частного положения;

определить видимость элементов фигур на чертеже, считая фигуры непрозрачными.

Исходные данные заданы численными значениями координат и сведены в таблицу № 1.

Видео:Построение треугольника в трёх проекцияхСкачать

ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ ЭПЮРА

Для выполнения графической работы студенту необходимо решить ряд задач.

Задача 1. Построение исходного чертежа многоугольника (рис. 1).

Горизонтальная проекция многоугольника ABCDE задана полностью, а фронтальная проекция только тремя проекциями точек А  В  Е . Необходимо достроить фронтальную проекцию точек С , D . При построении недостающей проекции заданного многоугольника необходимо соблюдать условие принадлежности точек данной фигуры к плоскости. Чтобы точки С, D лежали в плоскости, определенной тремя точками А , В и Е , необходимо, чтобы они находились на прямых, лежащих в этой плоскости. Этими прямыми являются диагонали АС , А D и ВЕ , горизонтальные проекции которых можно построить (рис. 1 а ).

Рис. 1. Построение исходного чертежа многоугольника:

а — построение недостающих проекций вершин многоугольника; б — пропорциональное деление отрезка BE

На фронтальной проекции пятиугольника проводят проекцию диагонали В  Е . В плоскости пятиугольника лежат точки пересечения диагоналей К и М , горизонтальные проекции которых К  и М  имеются, а фронтальные проекции получаются в результате пересечения линий проекционной связи, проведенных из К  и М , с диагональю В  Е . По двум точкам строятся фронтальные проекции других двух диагоналей А  К  и А  М , на них должны лежать проекции точек С  и D , которые определяются по их горизонтальным проекциям.

В случае, если линия совпадает по направлению с линией проекционной связи или круто наклонена к оси проекций, то недостающая проекция точки строится из условия пропорционального деления отрезка: если точка делит отрезок на пропорциональные части, то проекция этой точки делит проекции этого отрезка в том же отношении. На рис. 1 б нужно построить горизонтальную проекцию точки М . Из проекции точки В  проводят линию под углом меньше 90 к В  Е  и на ней от проекции точки В  откладывают отрезки равные В  М  и В  Е . Соединяют Е  и Е  и параллельно этому направлению проводят от М линию до пересечения с В  Е . Получают искомую горизонтальную проекцию М  .

Задача 2. Построить точку пересечения прямой MN с плоскостью треугольника АВ С.

Если прямая линия не параллельна плоскости, то она пересекает эту плоскость в действительной точке (см. рис. 2).

Рис. 2. Построение точки пересечения прямой с плоскостью

Алгоритм решения задачи:

1) Через заданную прямую MN проводим вспомогательную плоскость-посредник , перпендикулярную фронтальной плоскости проекций. Следовательно, на фронтальной плоскости проекций V все точки плоскости-посредника  будут проецироваться в прямую линию, совпадающую с фронтальной проекцией прямой M  N .

2) Находим линию пересечения вспомогательной плоскости-посредника  с заданной плоскостью треугольника АВС . На чертеже линия (1,2).

3) Находим искомую точку пересечения К прямой MN с плоскостью треугольника АВС . Она определяется как пересечение искомой прямой с найденной линией пересечения вспомогательной плоскости-посредника с плоскостью треугольника АВС .

Определение видимости на чертеже.

В начертательной геометрии плоскости считаются непрозрачными, поэтому необходимо на проекциях определить видимость.

Для определения видимости на чертеже используем метод конкурирующих точек, сущность которого заключается в выборе двух скрещивающихся прямых.

Для определения видимости на фронтальной плоскости проекций V поступают так. Выбираем две скрещивающиеся прямые В  С  и М  N , фронтальные проекции которых пересекаются в точках 1 и 3. По горизонтальной проекции определяем, что проекция точки 3, лежащая на проекции прямой M  N , будет закрывать проекцию точки 1, лежащую на проекции прямой В  С , т. к она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на фронтальной плоскости проекций проекция М  N  будет закрывать проекцию В  С . Границей видимости является проекция точки пересечения К.

Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А  С  и M  N , горизонтальные проекции которых пересекаются в точках 4 и 5. По фронтальной проекции определяем, что проекция точки 5, лежащая на проекции прямой М  N , будет закрывать проекцию точки 4, лежащую на проекции прямой А  С , т. к. она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на горизонтальной плоскости проекций проекция M  N  будет закрывать проекцию А  С . Границей видимости является проекция точки пересечения К .

Задача 3. Построение линии пересечения двух плоскостей, одна из которых занимает частное положение.

Даны две плоскости: плоскость ∆ АВС – плоскость общего положения, плоскость ∆ D ЕК – плоскость частного положения, которая расположена перпендикулярно фронтальной плоскости проекций (рис. 3).

Рис. 3. Построение линии пересечения двух плоскостей, одна из которых занимает
частное положение

Фронтальная проекция ∆ D ЕК совпадает с фронтальным следом плоскости и фронтальной проекцией линии пересечения треугольников.

( KL ) линия пересечения двух треугольников. Проекции этой линии пересечения – фронтальную и горизонтальную строят исходя из свойства принадлежности точек K и L сторонам ( АВ ) и ( ВС) , соответственно. Видимость треугольников на горизонтальной плоскости проекций определяем методом конкурирующих точек, рассмотренном в задаче 2.

Задача 4. Построение линии пересечения двух плоскостей общего положения.

Даны две плоскости общего положения, заданные треугольниками АВС и D ЕК . Построить линию пересечения двух треугольников, определить видимость треугольников на проекциях.

Прямая линия, получаемая при взаимном пересечении двух плоскостей, определяется двумя точками, каждая из которых одновременно принадлежит обеим плоскостям. Общие точки определяются решением основной позиционной задачи начертательной геометрии – построение точки пересечения прямой с плоскостью (см. рис. 2).

Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (проецирующие плоскости). Решение задачи приведено на рис. 4.

Алгоритм решения задачи:

1. Определяют первую точку линии пересечения двух треугольников – точку М .

1.1. Фронтально-проецирующая плоскость  проведена через сторону D К и задана на чертеже фронтальным следом  V .

1.2. Плоскость  пересекает плоскость треугольника АВС по прямой (1,2), на чертеже строят две проекции этой прямой.

1.3. Прямая (1,2) пересекает сторону D К в точке М , строят две проекции точки М  и М .

2. Определяют вторую точку искомой линии пересечения двух треугольников – точку N .

2.1. Горизонтально-проецирующая плоскость  проведена через сторону АВ и задана на чертеже горизонтальным следом  Н .

2.2. Плоскость  пересекает плоскость треугольника D ЕК по прямой (3,4), на чертеже строят две проекции этой прямой.

2.3. Прямая (3,4) пересекает АВ в точке N , строят две проекции точки N  и N .

Плоскости треугольников АВС и D ЕК пересекаются по прямой MN .

Рис. 4. Построение линии пересечения двух треугольников

3. Видимость плоских фигур на проекциях определяют методом конкурирующих точек.

Для определения видимости на фронтальной плоскости проекций V выбираем две скрещивающиеся прямые D  K  и A  B , фронтальные проекции которых пересекаются в точках 1 и 5. По горизонтальной проекции определяем, что проекция точки 5, лежащая на проекции прямой D  K , будет закрывать проекцию точки 1, лежащую на проекции прямой А  В , т. к. она будет ближе к наблюдателю. Следовательно, на фронтальной плоскости проекция D  K  будет закрывать проекцию A  B . Границей видимости является проекция линии пересечения M  N .

Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А  В  и D  Е , горизонтальные проекции которых пересекаются в точках 3 и 6. По фронтальной проекции определяем, что проекция точки 3, лежащая на проекции прямой D  Е , будет закрывать проекцию точки 6, лежащую на проекции прямой A  B , т.к. она будет ближе к наблюдателю. Следовательно, на горизонтальной плоскости проекция D  Е  будет закрывать проекцию А  В . Границей видимости является проекция линии пересечения N  M .

Задача 5. Построить две проекции линии пересечения плоскости  общего положения, заданной следами и плоскости  общего положения, заданной параллельными прямыми а и b .

Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (плоскости уровня), пересекающие заданные плоскости по прямым, недостающие проекции которых легко строятся и пересекаются в пределах чертежа.

Графическое решение задачи приведено на рис. 5.

Рис. 5. Построение линии пересечения двух плоскостей

Вспомогательная горизонтальная плоскость-посредник γ задана следом γ V и пересекает плоскость  по горизонтали, проходящей через точку 3, а плоскость  по горизонтали (1, 2). Горизонтальные проекции этих горизонталей пересекаются в точке К . Строят фронтальную проекцию точки К , используя свойство принадлежности точки прямой линии. Точка К принадлежит обеим плоскостям  и . Вторая точка N , общая для двух плоскостей  и , определяется второй вспомогательной плоскостью-посредником частного положения δ (на чертеже задана следом δ V ). Искомая прямая ( К N ) является линией пересечения двух плоскостей  и .

Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

ПРИЛОЖЕНИЕ 1

Видео:Построить линию пересечения треугольников ABC и DEF. Определить видимость. Вариант 2Скачать

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Гордон В.О., Семенцов-Огиевский М. А. Курс начертательной геометрии. Учеб. пособие. М.: Высшая школа. 2007.272 с.

2. Самохвалов Ю. И. Начертательная геометрия. Учебное пособие. Екатеринбург: Изд-во УГГУ. 2011. 121 с.

3. Самохвалов Ю. И., Шангина Е. И. Начертательная геометрия. Инженерная графика. Учебно-методическое пособие. Екатеринбург: Изд-во УГГУ. 2011. 96 с.

Видео:ЭПЮР 1Скачать

Московский государственный университет путей сообщения (МИИТ)

ЗАДАЧА№1

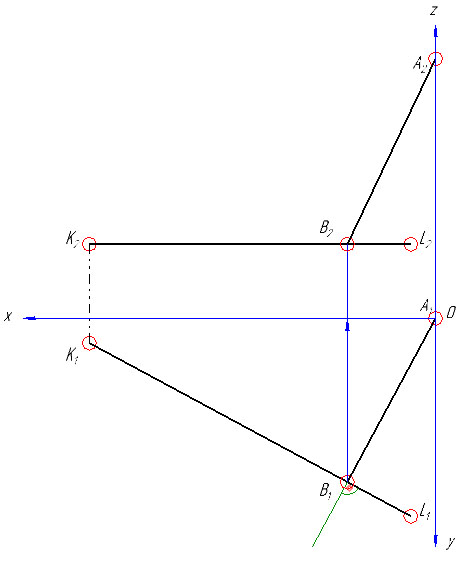
Построить проекции равнобедренного прямоугольного треугольника АВС, если известно, что катет ВС принадлежит прямой KL.

Исходными данными задачи является точка А – вершина треугольника и прямая KL, на которой расположен его катет ВС. Прямая KL – линия уровня (параллельна плоскости проекций П₁или П₂).

РЕШЕНИЕ:

1) По заданным координатам в таблице с вариантами строим проекции точек А, Р и прямой KL, в нашей задаче KL параллельна П₁ – т.е. горизонталь (координаты по оси z равны 30).

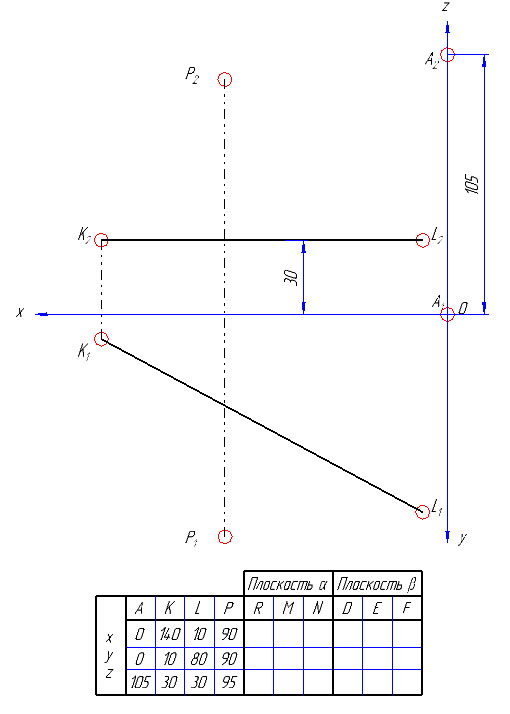
2) Из точки А опускаем перпендикуляр на прямую KL (так как искомый треугольник прямоугольный, а вершина А задана).

Отмечаем основание перпендикуляра – точку В (В₁). Фронтальную проекцию точки В (В₂) получаем по линии связи на К₂L₂.

3) Определяем натуральную величину катета АВ треугольника АВС способом прямоугольного треугольника: для этого на фронтальной проекции берем отрезок равный разнице координат проекций точек А и В – дельта z, и под прямым углом к горизонтальной проекции отрезка AB (A₁B₁) откладываем отрезок равный дельта z, получаем точку А₀. В₁А₀ – будет натуральной величиной катета (отрезка) АВ.

4) На прямой KL от точки В в любую сторону откладываем натуральную величину катета АВ (так как в равнобедренном прямоугольном треугольнике оба катета равны). В нашем случае откладываем на горизонтальной проекции K₁L₁ – т.к. KL – горизонталь и проецируется в натуральную величину именно на плоскость П₁. Получаем точку С (сначала проекцию С₁ и по линии связи C₂).

Соединяем точку А с точкой С. Треугольник АВС – искомый.

ЗАДАЧА№3

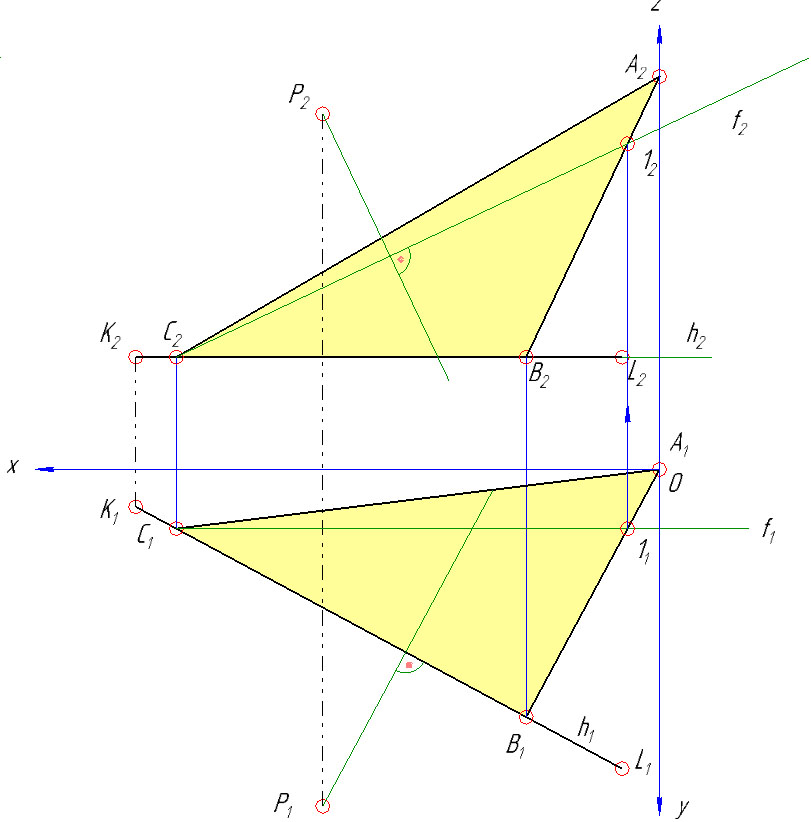
Определить натуральную величину расстояния от точки Р до плоскости.

РЕШЕНИЕ:

Кратчайшим расстоянием от точки до плоскости является отрезок перпендикуляра.

1) На основании теоремы о перпендикуляре к плоскости горизонтальная проекция перпендикуляра из точки Р проводится перпендикулярно к горизонтальной проекции горизонтали h. Независимо от горизонтальной проекции строится его фронтальная проекция. Для этого по плоскости найденного треугольника АВС проведена фронталь ƒ. Фронтальная проекция перпендикуляра должна быть перпендикулярна фронтальной проекции фронтали ƒ.

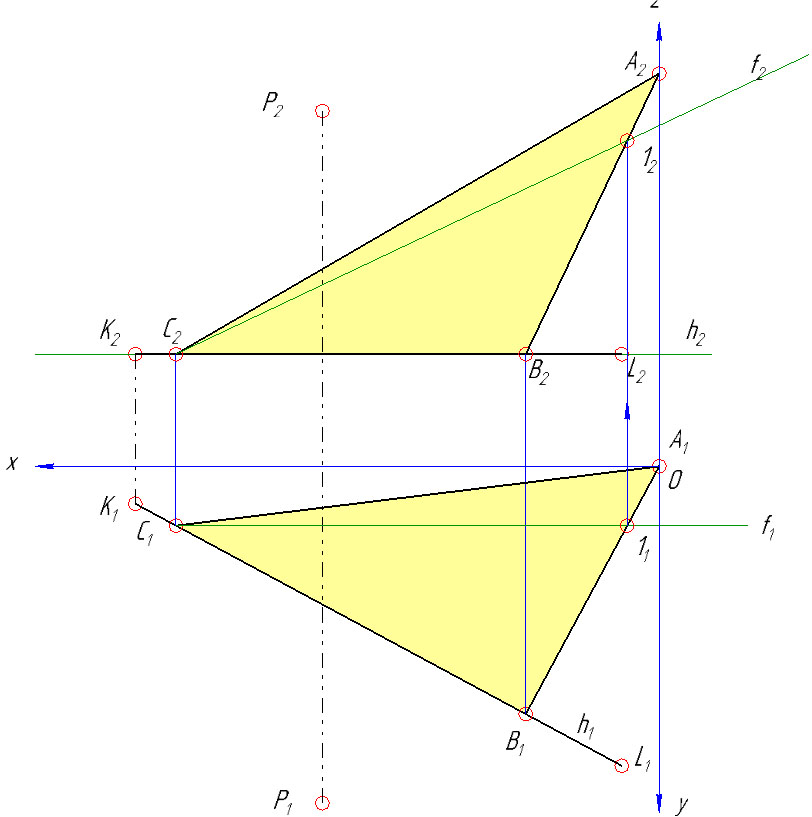
2) Прямая перпендикуляра из точки Р заключена в горизонтальнопроецирующую плоскость γ₁. Затем определена линия пересечения 2-3 вспомогательной плоскости γ с заданной плоскостью треугольника АВС.

В пересечении линии 2-3 с прямой n найдена искомая точка Q. Сначала определяется фронтальная проекция Q₂, а затем по линии проекционной связи определена ее горизонтальная Q₁ проекция.

3) Натуральная величина перпендикуляра PQ определена способом прямоугольного треугольника, аналогично как в задаче №1 определяли натуральную величину катета АВ.

Эпюра с задачами 1 и 3 — вариант 24

ЗАДАЧА №2.

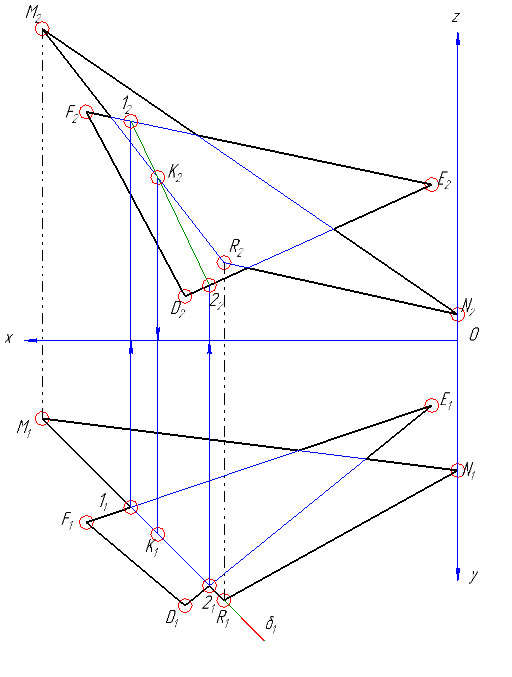
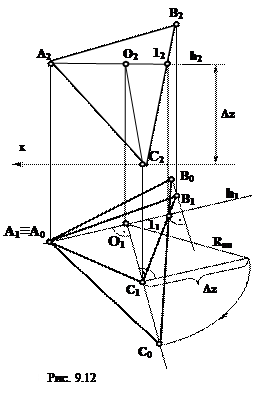
Построить линию пересечения двух плоскостей заданных треугольниками α(DEF) и β(RMN), координаты вершин которых заданы в таблице исходных данных.

РЕШЕНИЕ:

1) По заданным координатам строим проекции всех точек, получаем проекции треугольников DEF и RMN.

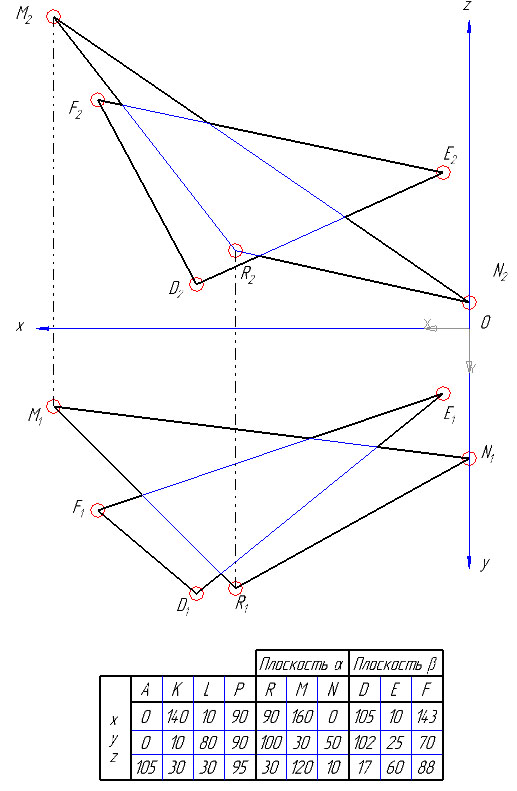
2) Решение задачи можно упростить, если вспомогательные проецирующие плоскости провести через прямые, задающие плоскость.

Так точка K этой линии определена с помощью горизонтальнопроецирущей плоскости δ₁, проведенной через сторону RM треугольника MNR. Именно линия RM является линией пересечения плоскости треугольника β(RMN) с вспомогательной плоскостью δ. Та же плоскость пересекает треугольник α(DEF) по линии 1-2.

Точка K, общая для трех плоскостей (двух заданных α и β и вспомогательной δ), находится в пересечении прямых 1-2 и RM.

Следует отметить, что если вспомогательная плоскость δ горизонтальнопроецирущая, то сначала определяется фронтальная проекция точки K₂, т.е. K₂ = 1₂-2₂∩R₂M₂, а затем по линии проекционной связи находится K₁ – горизонтальная проекция точки K.

3) Аналогично, заключая сторону DE во фронтальнопроецирующую плоскость γ₂, находится точка L. Прямая KL – линия пересечения заданных плоскостей.

4) Для определения видимости этих треугольников достаточно установить относительное расположение одной из сторон одного треугольника относительно стороны другого треугольника. Таким образом, вопрос видимости плоскостей сводится к определению видимости двух скрещивающихся прямых.

Определим видимость стороны DE треугольника DEF относительно стороны MN треугольника RMN на фронтальной плоскости проекции. Для этого проведем луч зрения s перпендикулярно П₂ через точку пересечения фронтальных проекций D₂E₂ и M₂N₂. В пересечении D₂E₂ и M₂N₂ расположены две конкурирующие по видимости точки (5₂ и 4₂). Точка 4 принадлежит стороне MN, а точка 5 – стороне DE. По горизонтальной проекции устанавливаем, что луч зрения сначала встретит D₁E₁ в точке 5₁, а затем M₁N₁ в точке 4₁. Следовательно, фронтальная проекция D₂E₂ – видима.

Аналогично определяется видимость треугольников и на горизонтальной проекции. Луч зрения при этом следует провести перпендикулярно к П₁ через две конкурирующие на П₁ точки скрещивающихся прямых (например, луч s / , проходящий через точки 1 и 6, соответственно принадлежащие прямым MR и ЕF).

Эпюр с задачей №2

ЗАКАЗЫВАЙТЕ ЧЕРТЕЖИ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ МГУПС

тел. (whatsup) 8-950-790-65-90

Видео:Построение следов плоскостиСкачать

Построить натуральную величину треугольника авс

Натуральная величина треугольника на эпюре Монжа может быть определена: – способом прямоугольного треугольника;

Здесь поочередно применяется способ прямоугольного треугольника для определения действительных величин отрезков, составляющих треугольник, а затем, к одному из них методом засечек строятся два других.

Используем Метод преобразования проекций для определения истиной величины треугольника на эпюре Монжа:

– Способ вращения вокруг осей перпендикулярных плоскостям проекций;

– Вращение вокруг горизонтали представляющих собой линии уровня;

представляющих собой линии уровня;

– Вращение вокруг следа или способ совмещения с плоскостью проекций;

Задача на определение натуральной величины плоской фигуры относится к разделу метрические задачи.

Ниже приведены решения одной и той же задачи вышеописанными методами.

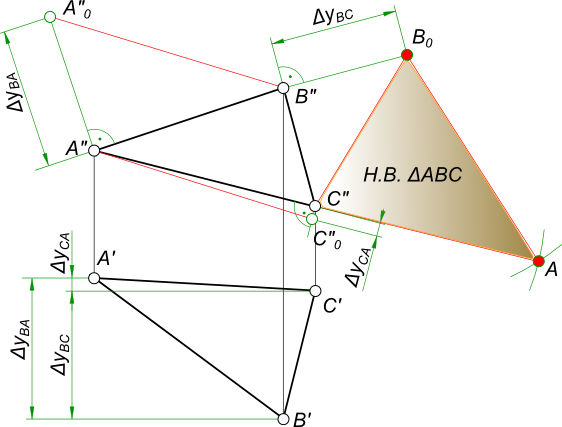
9.6.1. Задание:определить натуральную величину треугольника ABC(рис. 9.8), а также угол наклона плоскости треугольника к плоскости П₁_.

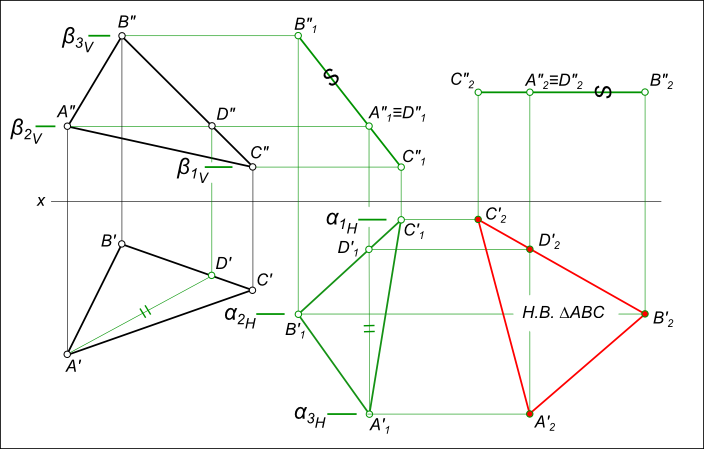
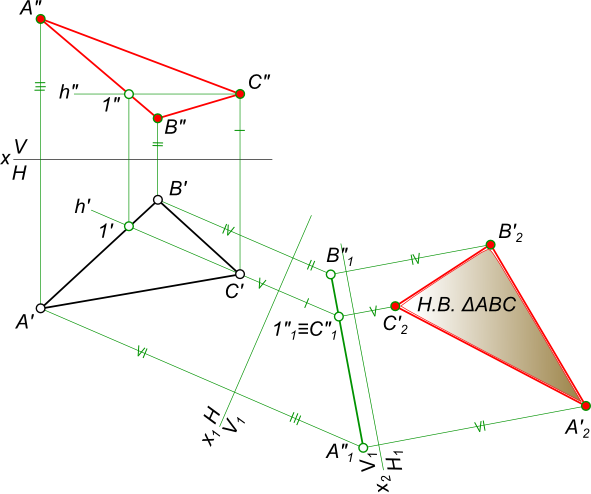
1) Решение методом замены плоскостей проекций (рис. 9.9).

Плоскость треугольника спроецируется в натуральную величину в том случае, если она будет параллельна одной из плоскостей проекций. Одним преобразованием задачу решить невозможно. Она решается в два этапа: при первой замене плоскостей проекций получают плоскость треугольника ABC,перпендикулярную к новой плоскости проекций, при второй замене – получают плоскость треугольника, параллельную новой плоскости проекций.

Первый этап. Одним из условий перпендикулярности двух плоскостей является наличие прямой, принадлежащей одной из плоскостей, перпендикулярной к другой плоскости. Используя этот признак, проводят через точку А в плоскости треугольника горизонталь (h). Затем на произвольном расстоянии от горизонтальной проекции треугольника A₁B₁C₁ проводят ось x_1,4новой системы плоскостей проекций П₁/П₄перпендикулярно к горизонтальной проекции горизонтали h₁.В новой системе треугольник ABC стал перпендикулярен к новой плоскости проекций П₄.

На линиях проекционной связи в новой системе откладывают координатыzточек А, В, С с фронтальной проекции исходной системы плоскостей П₁/П₂.

При соединении новых проекций А₄,B₄, С₄получают прямую линию, в которую спроецировался треугольник ABC. На этом этапе определяется угол наклона плоскости треугольника к горизонтальной плоскости проекции П₁ – угол α. На чертеже это угол между осью x_1,4и проекцией С₄А₄В₄.

Второй этап. Выбираем новую плоскость проекции П₅,параллельную плоскости треугольника, т.е. новую ось x_4,5проводят параллельно С₄А₄В₄на произвольном расстоянии. Получают новую систему П₄/П₅.Полученный треугольник А₅В₅С₅и есть искомая натуральная величина треугольника ABC.

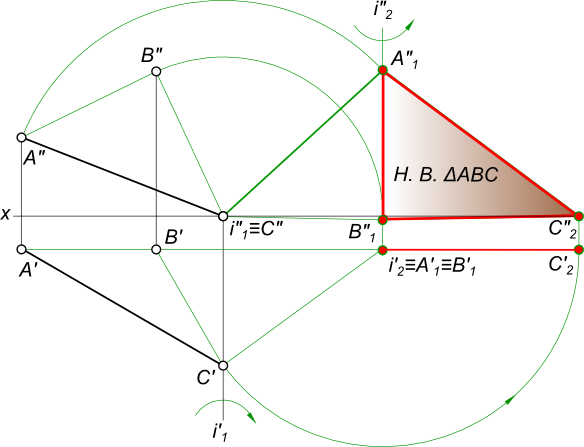
2) Решение методом вращения вокруг проецирующей оси(рис. 9.10).

Задача решается в два этапа. На первом этапе выполняют вращение так, чтобы плоскость треугольника ABCпреобразовалась в проецирующую плоскость, т.е. стала перпендикулярна к одной из плоскостей проекций. Для этого проводят горизонталь h (h₁,h₂) через точку А. (построение начинают с фронтальной проекции h₂,она проходит через проекцию точки A₂и проекцию точки 1₂ при этомh₂ параллельна оси х).Далее находят горизонтальную проекцию h₁ горизонтали h (через проекции A₁ и 1₁). Через точку А проводят ось i – ось вращения треугольника так, чтобы она была перпендикулярна к П₁. На фронтальной проекции через вершины А₂ и В₂ проводят следы горизонтальных плоскостей уровня Δ и Σв которых при вращении будут перемещаться точки АиВ. Вершина С принадлежит плоскости П₁поэтому ее плоскостью вращения будет плоскость проекций П₁.На горизонтальной проекции, взяв за центр вращения проекцию i₁ поворачивают горизонталь А так, чтобы на плоскость П₂ она спроецировалась в точку. На чертеже это выразится 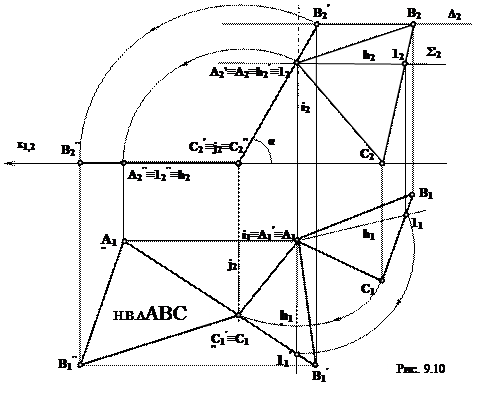тем, что h’₁ займет новое положение – перпендикулярно к оси х.

При этом на фронтальной проекции А₂ остается неизменной, находясь на следе плоскости Σ₂ и ее обозначим a₂‘.

На горизонтальной проекции поворачиваем оставшиеся вершины В и С вокруг оси i так, чтобы . На фронтальной проекции вершина В перемещается по следу плоскости ₂, а вершина С – по оси х. Соединив новые положения проекций всех вершин треугольника ABC, получают проекцию А’₂В’₂С’₂,сливающуюся в линию. Плоскость треугольника ABC заняла проецирующее положение. На данном этапе, при необходимости, находят угол наклона плоскости треугольника ABC к П₁ – угол α .

На втором этапе проводят ось jчерез вершинуС так, чтобы ось была фронтально проецирующая. При этом С’₂ ≡ j’₂, а горизонтальная проекция j’₁ пройдет через проекцию С’₁. Вокруг оси поворачивают треугольник так, чтобы он стал параллелен горизонтальной плоскости проекций. В данной задаче вращают точки А’₂ и В’₁, вокруг j₂ до совмещения с осью х,при этом проекции B’₁ и A’₁ будут перемещаться параллельно оси хи займут новое положение В»₁, и А»₁ вершина С останется на месте. Соединив точки между собой, получают новое положение плоскости (оно соответствует натуральной величине треугольника ABC).

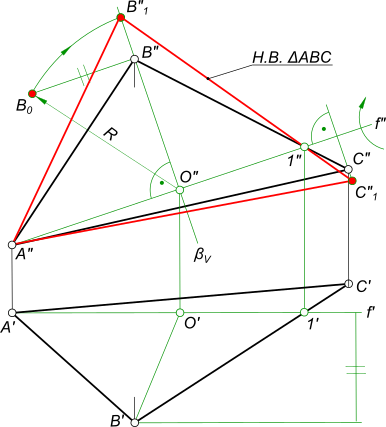
3) Решение методом плоскопараллельного перемещения (рис. 9.11).

Задача решается в два этапа. На первом этапе преобразуют чертеж так, чтобы плоскость треугольника ABC стала перпендикулярна к одной из плоскостей проекций. Для этого проводят в плоскости треугольника горизонталь h (фронтальная проекция А₂1₂║х,). Каждую вершину треугольника заключают в свою плоскость уровня, параллельную плоскости П₁. В рассматриваемом примере вершина С принадлежит плоскости проекций П₁, А принадлежит плоскости Σ, В — плоскости Δ.

Плоскость треугольника перемещается в пространстве до тех пор, пока горизонталь h₁ треугольника не станет перпендикулярна к фронтальной плоскости проекций П₂.

Для этого на свободном поле чертежа вычерчивают горизонтальную проекцию треугольника A₁ ′ B₁ ′ C₁ ′ с условием, чтобы А₁1₁П₂, а значит А₁ ′ 1₁ ′ х. При этом вершины треугольника, перемещаясь каждая в своей плоскости, займут новое положение – (фронтальная проекция А₂В₂С₂ заменится А’₂В’₂С’₂).Соединив эти точки, получают новое положение треугольника ABC, спроецированного в линию, т.е. перпендикулярного к плоскости П₂.

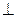
На втором этапе, чтобы получить натуральную величину треугольника ABC, его плоскость поворачивают до тех пор, пока она не будет параллельна одной из плоскостей проекций. В рассматриваемом решении фронтальную проекцию треугольника А₂‘В₂‘С₂‘располагают на произвольном расстоянии от оси хпараллельно плоскости П₁. При этом вершины А, Ви С треугольника заключают в горизонтально проецирующие плоскости θ, Т, Р. По следам этих плоскостей будут перемещаться горизонтальные проекции вершин А₁‘В₁‘С₁‘. От нового положения фронтальной проекции А₂«В₂«С₂« проводят линии проекционной связи до пресечения с соответствующими следами плоскостей, в которых они перемещаются (θ₁,T₁,P₁), и получая проекции точек А₁» В₁» C₁«. Соединив эти проекции, получают треугольник ABC в натуральную величину.

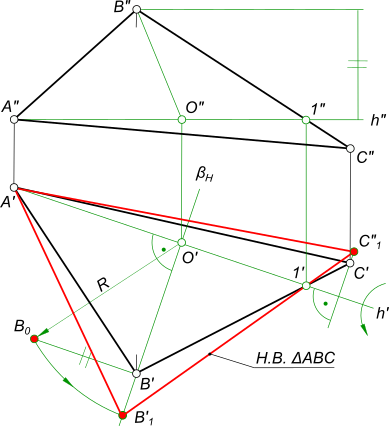
4) Решение методом вращения вокруг линии уровня(рис.9.12)

Для решения задачи этим способом необходимо повернуть плоскость треугольника вокруг линии уровня, в данном случае вокруг горизонтали, до положения, параллельного горизонтальной плоскости проекции. Через точку А в плоскости треугольника ABC проводят горизонталь h, фронтальная проекция которой будет параллельна оси х. Отмечают точку 1₂ и находят ее горизонтальную проекцию 1₁. Прямая A₁1₁ является горизонтальной проекцией h₁горизонтали h. Вокруг горизонтали будут вращаться точки В и С. Определяют натуральную величину радиуса вращения точки С .

Для определения натуральной величины радиуса вращения используют любой метод (в данном случае способ прямоугольного треугольника) строят прямоугольный треугольник, в котором O₁C₁ – один из катетов. Второй катет – разность координат Δzотрезка О₂С₂, взятого с фронтальной проекции. В построенном треугольнике гипотенуза O₁C – натуральная величина радиуса вращения.

На продолжении перпендикуляра O₁C₁ откладывают |R_Bp.| и получают новое положение вершины С после вращения — С . Проекция вершины В получается пересечением луча C 1₁ и перпендикуляра к горизонтальной проекции h₁ проведенного через проекцию точки В₁.

Треугольник A B C есть искомая натуральная величина треугольника ABC.

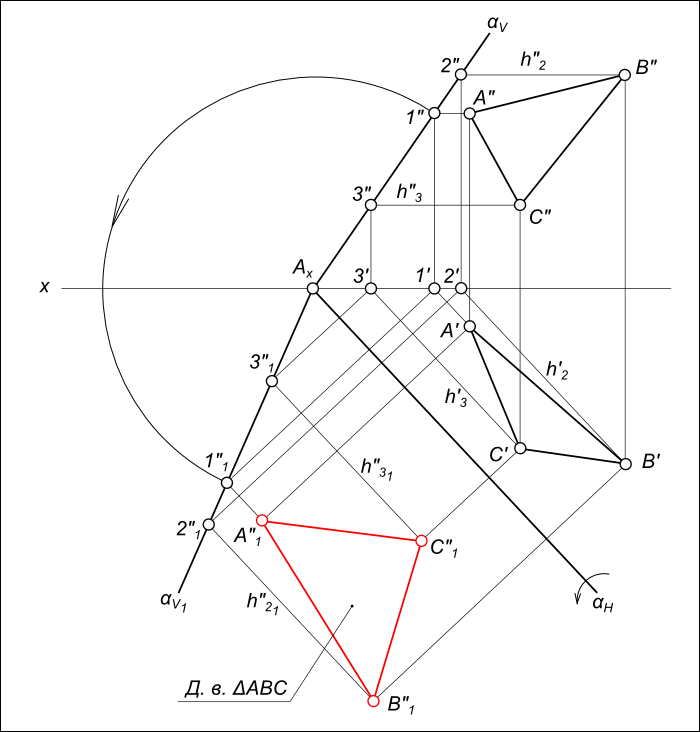
5) Решение методом совмещения(рис. 9.13).

Для решения задачи методом совмещения необходимо построить следы плоскости Σ, которой принадлежит треугольник ABC. Для этого проводят в плоскости треугольника ABC фронталь f и находят горизонтальный след этой фронтали – N₁. По условию задачи вершина С треугольника принадлежит горизонтальной плоскости проекций П₁. Тогда горизонтальный след Σ₁ плоскости Σпроводят через проекции N₁ и C₁. Соединив эти две точки и продлив отрезок до пересечения с осью х, находят точку схода следов Σ_х. Учитывая, что все фронтали плоскости параллельны ее фронтальному следу, фронтальный след Σ₂ плоскости Σпроводят через точку Σ_хпараллельно проекции фронтали f₂.

Для нахождения натуральной величины треугольника ABCнеобходимо построить совмещенное положение плоскости Σ с горизонтальной плоскостью проекций П₁. Для этого через вершину Апроводят горизонталь h₁. На фронтальном следе Σ₂ фиксируют точку 2₂. Ее горизонтальная проекция – точка 2₁. Точка 2 вращается в плоскости, перпендикулярной к горизонтальному следу плоскости Σ. Поэтому, чтобы построить точку 2 в совмещенном положении 2 , проводят из 2₁перпендикуляр к горизонтальному следу Σ, а из центра Σ_х дугу окружности радиусом Σ_х2₂ до пересечения с направлением перпендикуляра. Соединив Σ_х с 2 , получают совмещенное положение фронтального следа Σ – Далее через точку 2 проводят горизонталь h всовмещенном положении. На этой горизонтали находят точку А , проведя перпендикуляр из точки A₁ к горизонтальному следу Σ₁.

По такой же схеме строят совмещенное положение точки В . Совмещенное положение точки С совпадает с ее горизонтальной проекцией С₁ т.е. С₁≡С . Соединив построенные точки, получают треугольник А В С – это и есть натуральная величина треугольника ABC.

Не нашли то, что искали? Воспользуйтесь поиском:

Метки

Видео:Линия пересечения плоскостейСкачать

Натуральная величина треугольника с описанием.

Натуральная величина треугольника определяется 2 методами:

замена плоскостей проекции;
плоскопараллельное перемещение.

Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».

Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.

Алгоритм определения натуральной величины плоскости:

Замена плоскостей проекции

1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.

2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.

3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:

от С2 до оси Х;
от В2 до оси Х;
от А0 до оси Х.

Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.

4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.

5.) Отмеряются расстояния:

от В1 до Х1;
от С1 до Х1;
от А1 до Х1.

Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).

6.) Соединяются точки и подписывают полученную плоскость заглавными «Н.В.»

Плоскопараллельное перемещение

7.) Откладывается отрезок на оси Х (обозначен синим цветом).

8.) Переносятся точки на текущее построение.

9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 10.) Методом вращения точки А2′, С2′ переносятся на горизонтальную прямую, а точка В2′ не меняет свое положение (относительно ее и происходило вращение).11.) Откладывается точка (располагают от оси Х на небольшом расстоянии, т.е. произвольном), относительно которой и будет откладываться плоско параллельное перемещение плоскости. 12.) От точек А2′, С2′ и В2′ опускаются прямые. Далее циркулем необходимо отмерить расстояния:

Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).

13.) Соединяются и подписываются точки (А1′, В1′ и С1′). Опускают прямые от С2″ и А2″14.) От точек С1 и А1 отводят прямые до пересечения с прямыми опущенными от точек С2″ и А2″. В месте пересечения ставится точка.15.) Завершающим шагом является соединение точек и обводка линиями всего чертежа.Пример чертежа на тему «Натуральная величина треугольника» смотрите здесь.