Дана равнобедренная трапеция окружность построенная на боковой стороне (2 видео)

Дана равнобедренная трапеция окружность построенная на боковой стороне

Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром O, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке H, точка Q — середина MN.

а) Докажите, что четырёхугольник NQOH — параллелограмм.

б) Найдите KN, если ∠LKN = 75° и LM = 2.

а) Треугольник KOH равнобедренный и трапеция KLMN равнобедренная, поэтому ∠KHO = ∠OKH = ∠MNK. Значит, прямые OH и MN параллельны, а так как OQ — средняя линия трапеции, то параллельны прямые OQ и KN. Противоположные стороны четырёхугольника NQOH попарно параллельны, следовательно, NQOH — параллелограмм.

б) Пусть окружность с центром в точке O радиуса R касается стороны MN в точке P. В прямоугольных треугольниках OPQ и KHL имеем

Пусть KH = x. Поскольку трапеция KLMN равнобедренная, KN = 2KH + LM; NH = KH + LM = x + 2.

откуда x = 2. Значит, KN = 2x + 2 = 6.

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Задача 16760 Дана равнобедренная трапеция KLMN с. Условие Решение Дана равнобедренная трапеция окружность построенная на боковой стороне 💡 Видео Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать Задача 16760 Дана равнобедренная трапеция KLMN с. Условие Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром О, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке Н, точка Q — середина MN. а) Докажите, что четырёхугольник NQOH — параллелограмм. б) Найдите KN, если угол LKN = 75° и LM = 4. Решение OQ-средняя линия трапеции KLMN OQ\|\|LM OQ\|\|KN ⇒ OQ\|\|HN OK=OL=OH=OB=r Δ KOH- равнобедренный (ОК=ОН=r) ∠ OKH=∠OHK=75 градусов; ∠OHK=∠QNK=75 градусов, это односторонние углы, значит OH\|\|QN NQOH- параллелограмм, так как противоположные стороны попарно параллельны: OQ\|\|HN и OH\|\|QN б) Дано: ∠ LKN=∠MNK=75 градусов; LM=4 Пусть боковые стороны трапеции LK и MN пересекаются в точке А. ∠ АLМ=∠ LKN=75 градусов; ∠АML=∠MNK=75 градусов; Значит, ∠ АLМ=∠АML=75 градусов; Δ ALM — равнобедренный ∠ LAM=180 градусов — ∠ АLМ-∠АML=180 градусов -75 градусов-75 градусов=30 градусов; ΔАОВ- прямоугольный (OB⊥MN) с острым углом ∠ LAM=30 градусов, катет против угла в 30 градусов равен половине гипотенузы ОА=2ОВ=2r Тогда AL=AO-LO=2r-r=r AL=AM=r LM- средняя линия треугольника AOQ OQ=2LM=2*4=8 ΔАLM=ΔKOH AL=AM=OK=OH=r LM=KH=4 Видео:Геометрия Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром OСкачать Дана равнобедренная трапеция окружность построенная на боковой стороне Вопрос по геометрии: Пожалуйста,решите,мне нужно с рисунком. ☺Дана равнобедренная трапеция ABCD с основаниями AD и BC. ОКРУЖНОСТЬ с центром O,построенная на боковой стороне AB как на диаметре,касается боковой стороны и второй раз пересекает большее основание AD в точке H,точка Q -середина CD. 1)Докажите,что четырехугольник DQOH-параллелограмм 2)НАЙДИТЕ AD,если угол Bad =60° и BC=2 Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ? Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно! Ответы и объяснения 1 Введем дополнительные обозначения: Пусть окружность касается стороны CD в точке К, ОЕ1 и ОЕ2 — высоты трапеции АОQD a) по условию АВ-диаметр окружности, значит АО=ОВ=R ABCD — равнобедренная трапеция, следовательно ∠ВАD=∠CDA и AB=CD=2R Если Q — середина CD, то ОQ — средняя линия трапеции. Следовательно AO=OB=CQ=QD=R Также АО=ОН=R, то есть ΔАОН-равнобедренный, значит ∠ВАD=∠OHA При этом ∠ВАD=∠CDA, следовательно ∠OHA=∠CDA, значит эти углы соответственные при параллельных прямых ОН и DQ и секущей АD. Итак, ОН=QD и ОН \|\| QD, следовательно DQOH-параллелограмм. б) ∠ВАD=∠OHA=60° ∠АОН=180°-(∠ВАD+∠OHA)=180°-(60°+60°)=60° — ΔАОН — равносторонний, следовательно АН=R ∠ABC=∠BCD=180°-60°=120° Если окружность касается CD, то ∠OKC=90° и ОК=R Сумма всех углов в четырехугольнике равна 360° ∠ВОК=360°-(∠ОВС+∠OKC+∠DCK)=360°-(120°+90°+120°)=30° Если ОQ -средняя линия трапеции, то OQ \|\| AD, следовательно ∠BAD=∠BOQ=60° ∠KOQ=∠BOQ-∠ВОК=60°-30°=30° ΔOQK -прямоугольный с прямым углом OKQ 💡 Видео СЕРЬЁЗНО готовимся к ОГЭ 2024! / Полный прогон задания 17 на ОГЭ по математикеСкачать ЕГЭ, задача 16 (продолжение: "Планиметрия вокруг окружности")Скачать ЕГЭ Задание 16 Трапеция и две окружностиСкачать 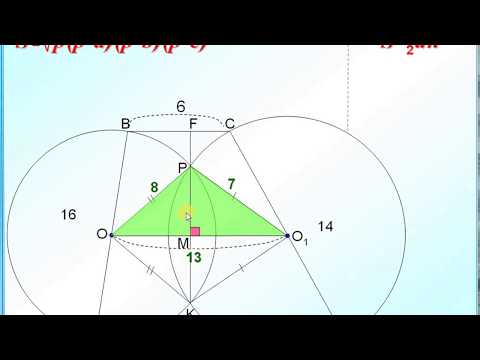8 класс, 6 урок, ТрапецияСкачать Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать №1034. В равнобедренной трапеции меньшее основание равно боковой стороне, большее основаниеСкачать РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ. Школьная задача! Вспомним детство!Скачать СЕЧЕНИЯ. СТРАШНЫЙ УРОК \| Математика \| TutorOnlineСкачать Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать №799. Дана равнобедренная трапеция ABCD. Перпендикуляр, проведенный из вершины В к большему основаниСкачать Всё про углы в окружности. Геометрия \| МатематикаСкачать Задача 16 (планиметрия) ЕГЭ 2017 #1Скачать Задание второй части реального варианта ЕГЭ 2015 Планиметрия #3Скачать Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать 🔴 В прямоугольной трапеции основания ... \| ЕГЭ БАЗА 2018 \| ЗАДАНИЕ 15 \| ШКОЛА ПИФАГОРАСкачать Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать Поделиться или сохранить к себе: Search for: Треугольник Найдите площадь треугольника кмп 828 Окружность Координаты пересечения отрезка и окружности 834 Вектор Развертки коробок в векторе 862 Вектор Ошибки в комбайне вектор Четырехугольники Стороны четырехугольника стягивают дуги описанной окружности 63 62 828 Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности О сайте \| \| © 2024 Курс школьной геометрии.

Критерии оценивания выполнения задания

Баллы

Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)

Получен обоснованный ответ в пункте б)

имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Содержание

Задача 16760 Дана равнобедренная трапеция KLMN с.
Условие
Решение
Дана равнобедренная трапеция окружность построенная на боковой стороне
💡 Видео

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Задача 16760 Дана равнобедренная трапеция KLMN с.

Условие

Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром О, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке Н, точка Q — середина MN.

а) Докажите, что четырёхугольник NQOH — параллелограмм.

б) Найдите KN, если угол LKN = 75° и LM = 4.

Решение

OQ-средняя линия трапеции KLMN
OQ||LM
OQ||KN ⇒ OQ||HN
OK=OL=OH=OB=r
Δ KOH- равнобедренный (ОК=ОН=r)
∠ OKH=∠OHK=75 градусов;

∠OHK=∠QNK=75 градусов, это односторонние углы, значит
OH||QN
NQOH- параллелограмм, так как противоположные стороны попарно параллельны:
OQ||HN
и
OH||QN

б)
Дано:
∠ LKN=∠MNK=75 градусов;
LM=4

Пусть боковые стороны трапеции LK и MN пересекаются в точке А.
∠ АLМ=∠ LKN=75 градусов;
∠АML=∠MNK=75 градусов;
Значит, ∠ АLМ=∠АML=75 градусов;
Δ ALM — равнобедренный
∠ LAM=180 градусов — ∠ АLМ-∠АML=180 градусов -75 градусов-75 градусов=30 градусов;

ΔАОВ- прямоугольный (OB⊥MN) с острым углом ∠ LAM=30 градусов, катет против угла в 30 градусов равен половине гипотенузы
ОА=2*ОВ=2*r

Тогда AL=AO-LO=2r-r=r
AL=AM=r
LM- средняя линия треугольника AOQ
OQ=2LM=2*4=8

ΔАLM=ΔKOH
AL=AM=OK=OH=r
LM=KH=4

Видео:Геометрия Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром OСкачать

Дана равнобедренная трапеция окружность построенная на боковой стороне

Вопрос по геометрии:

Пожалуйста,решите,мне нужно с рисунком. ☺Дана равнобедренная трапеция ABCD с основаниями AD и BC. ОКРУЖНОСТЬ с центром O,построенная на боковой стороне AB как на диаметре,касается боковой стороны и второй раз пересекает большее основание AD в точке H,точка Q -середина CD.
1)Докажите,что четырехугольник DQOH-параллелограмм
2)НАЙДИТЕ AD,если угол Bad =60° и BC=2

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Введем дополнительные обозначения:
Пусть окружность касается стороны CD в точке К, ОЕ1 и ОЕ2 — высоты трапеции АОQD
a) по условию АВ-диаметр окружности, значит АО=ОВ=R
ABCD — равнобедренная трапеция, следовательно ∠ВАD=∠CDA и AB=CD=2R
Если Q — середина CD, то ОQ — средняя линия трапеции. Следовательно AO=OB=CQ=QD=R
Также АО=ОН=R, то есть ΔАОН-равнобедренный, значит
∠ВАD=∠OHA
При этом ∠ВАD=∠CDA, следовательно ∠OHA=∠CDA, значит эти углы соответственные при параллельных прямых ОН и DQ и секущей АD.
Итак, ОН=QD и ОН || QD, следовательно DQOH-параллелограмм.

б) ∠ВАD=∠OHA=60°
∠АОН=180°-(∠ВАD+∠OHA)=180°-(60°+60°)=60° — ΔАОН — равносторонний, следовательно АН=R
∠ABC=∠BCD=180°-60°=120°
Если окружность касается CD, то ∠OKC=90° и ОК=R
Сумма всех углов в четырехугольнике равна 360°
∠ВОК=360°-(∠ОВС+∠OKC+∠DCK)=360°-(120°+90°+120°)=30°
Если ОQ -средняя линия трапеции, то OQ || AD, следовательно
∠BAD=∠BOQ=60°
∠KOQ=∠BOQ-∠ВОК=60°-30°=30°
ΔOQK -прямоугольный с прямым углом OKQ