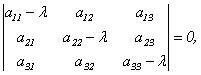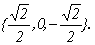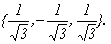Симметричная матрица собственные вектора

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Страница — в разработке. Начало работ — 08.03.2014, окончание — .

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Симметричная матрица

Теорема. Для любой матрицы $ A_ $ матрицы $ A_A^ $ и $ A^ A $ — симметричны. Для любой квадратной матрицы $ A_ $ матрица $ A_+A^ $ — симметрична.

Видео:Собственные значения и собственные векторыСкачать

Определитель

Теорема [Кэли]. В полном разложении определителя симметричной матрицы порядка $ n $ обозначим $ mathfrak s_n $ число слагаемых, $ mathfrak s_n^ $ — число слагаемых с положительным знаком, $ mathfrak s_n^ $ — число слагаемых с отрицательным знаком, а $ mathfrak d_n =mathfrak s_n^ — mathfrak s_n^ $. Имеют место соотношения:

$$ mathfrak s_=(n+1)mathfrak s_n- C_n^2 mathfrak s_ ; $$ $$ mathfrak d_=-(n-1)mathfrak d_n- C_n^2 mathfrak d_ . $$

Имеют место пределы:

Миноры: тождества Кронекера

Теорема [Кронекер]. Для симметричной матрицы $ A_ $ порядка $ n ge k+1 $ имеет место тождество

$$ Aleft(begin 1 & 2 & dots & k-2 & k \ 2 & 3 & dots & k-1 & k+1 end right)- Aleft(begin 2 & 3 & dots & k-1 & k \ 1 & 2 & dots & k-2 & k+1 end right)= $$ $$ = Aleft(begin 1 & 2 & dots & k-3 & k-2 & k-1 \ 2 & 3 & dots & k-2 & k & k+1 end right) , $$ связывающее три ее минора порядка $ k-1 $.

Пример. Для $ k=4 $:

$$ Aleft(begin 1 & 2 & 4 \ 2 & 3 & 5 end right)- Aleft(begin 2 & 3 & 4 \ 1 & 2 & 5 end right)= Aleft(begin 1 & 2 & 3 \ 2 & 4 & 5 end right) $$ $$ iff left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right|- left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right|= left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right| . $$

В настоящем разделе минор матрицы $ A $ $$ Aleft( begin j_1 & dots & j_k \ j_1 & dots & j_k end right) = left|begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ vdots & & ddots & vdots \ a_ & a_ & dots & a_ end right| , quad 1le j_1 ☞ ЗДЕСЬ.

Теорема. Если $ mathfrak r = operatorname (A)ge 1 $, то в матрице $ A $ существует ненулевой ведущий минор порядка $ mathfrak r $.

Видео:Собственные векторы и собственные значения матрицыСкачать

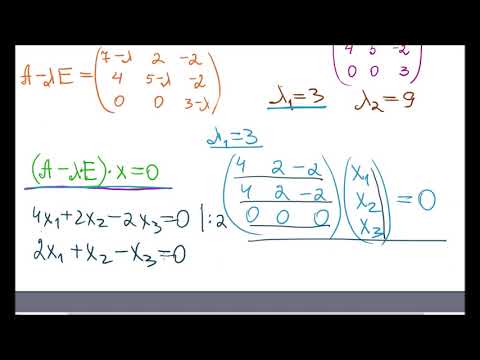
Произведение

Теорема. Для того, чтобы произведение симметричных матриц $ A $ и $ B $ было симметричной матрицей необходимо и достаточно, чтобы матрицы $ A $ и $ B $ коммутировали: $ AB = BA $.

Видео:А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

Обратная матрица

Теорема. Обратная к симметричной матрице (если существует) будет симметричной матрицей.

Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Характеристический полином, собственные числа, собственные векторы

Теорема 1. Все собственные числа симметричной матрицы вещественны.

Доказательство ☞ ЗДЕСЬ.

Если $ lambda=0 $ корень кратности $ mathfrak m $ характеристического полинома симметричной матрицы $ A $, т.е.

$$ det (A-lambda E)equiv(-1)^n lambda^n+a_1lambda^+dots+a_ lambda^ quad npu a_ne 0 $$ то $ operatorname (A)=n-mathfrak m $.

Если в характеристическом полиноме некоторый коэффициент $ a_j $ при $ j notin $ обращается в нуль, то соседние с ним в нуль не обращаются и имеют различные знаки: $ a_ a_ ♦

Локализация собственных чисел

Теорема [Коши]. Для симметричной матрицы $ A_ $ число ее собственных чисел, лежащих на интервале $ ]a,b_[ $, определяется по формуле:

Согласно этой теореме, главные миноры матрицы $ A-lambda, E $ играют роль системы полиномов Штурма для характеристического полинома симметричной матрицы $ A_ $.

$$ A_1,A_2,dots,A_ $$ симметричной матрицы $ A_ $ отличны от нуля, то число положительных собственных чисел матрицы $ A_ $ равно числу знакопостоянств, а число отрицательных собственных чисел — числу знакоперемен в ряду $ 1,A_1,dots,A_n $:

Часто в приложениях требуется вычислить значения не всех собственных чисел симметричной матрицы, а только небольшого (по сравнению с порядком матрицы) количества максимальных по модулю. Численный метод решения этой задачи изложен ☞ ЗДЕСЬ.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Диагонализуемость

Теорема. Существует ортогональная матрица $ P_ $, приводящая симметричную матрицу $ A_ $ к диагональному виду:

$$ P^AP=P^<^>AP= left( begin lambda_1 & & & mathbb O \ & lambda_2 & & \ && ddots & \ mathbb O&& & lambda_n end right). $$

Доказательство особенно просто в случае когда все собственные числа $ lambda_1,dots, lambda_n $ различны. На основании теоремы 1 матрица $ A_ $ диагонализуема над множеством вещественных чисел и на основании теоремы 2 матрица $ P $, приводящая к диагональному виду, может быть выбрана ортогональной.

Для общего случая доказательство производится индукцией по порядку $ n $ матрицы $ A $. Окончание доказательства ☞ ЗДЕСЬ. ♦

Теорема утверждает что даже при наличии кратных корней у характеристического полинома $$ f(lambda)=(-1)^n(lambda — lambda_1)^<_1> times dots times (lambda — lambda_)^<_>, quad _1+dots+_<>=n, lambda_k ne lambda_ npu k ne ell $$ алгебраическая кратность собственного числа $ lambda_j $ совпадает с его геометрической кратностью: $$operatorname , (A-lambda_j, E)= _j, npu quad forall jin .$$ Или, что то же: размерность собственного подпространства $$ left <Xin mathbb R^n , big| , (A-lambda_j, E)X=mathbb O_right> $$ равна $ _j $. При нахождении фундаментальной системы решений (ФСР) указанной системы уравнений мы получим $ _j $ линейно независимых собственных векторов $ <_,dots, _<j_j> > $ , принадлежащих $ lambda_j $. Однако при традиционных способах построения ФСР вовсе не гарантирована ортогональность этих векторов. Как построить ФСР так, чтобы она удовлетворяла условию теоремы, т.е. была ортонормированной? Воспользуемся для этого процессом ортогонализации Грама-Шмидта, применив его к системе $ <_,dots, _<j_j> > $. Результатом процесса будет новая система векторов $ <_,dots, _<j _j> > $ такая что ее линейная оболочка совпадает с линейной оболочкой исходной системы: $$ left(_,dots, _<j _j> right)= left(_,dots, _<j_j> right) quad mbox quad langle _,_ rangle =0 mbox k ne ell , , $$ т.е. векторы $ _,dots, _<j _j> $ остаются собственными векторами, принадлежащими $ lambda_j $. Но теперь эти новые векторы попарно ортогональны. Нормировав их, мы получим требуемую теоремой систему из $ _j $ ортогонормированных столбцов матрицы $ P $, соответствующих кратному собственному числу $ lambda_j $.

Пример. Диагонализовать матрицу

$$ A=left( begin 0&1&0&1&0&0&0&-1 \ 1&0&1&0&0&0&-1&0 \ 0&1&0&1&0&-1&0&0 \ 1&0&1&0&-1&0&0&0 \ 0&0&0&-1&0&1&0&1 \ 0&0&-1&0&1&0&1&0 \ 0&-1&0&0&0&1&0&1 \ -1&0&0&0&1&0&1&0 end right) $$ с помощью ортогональной матрицы.

Решение. Имеем: $$ det (A-lambda E) equiv (lambda-3)(lambda+3)(lambda-1)^3(lambda+1)^3 , . $$ Ищем собственные векторы. Для простых собственных чисел: $$ lambda_1=-3 Rightarrow mathfrak X_1=left[1,-1,1,,-1,-1,1,-1,1right]^ ; $$ $$ lambda_2=3 Rightarrow mathfrak X_2=left[-1,-1,-1,-1,1,1,1,1right]^ . $$ Эти столбцы войдут в состав матрицы $ P $, только их надо нормировать: $ mathfrak X_ /|mathfrak X_| $. Для кратных собственных чисел $ lambda_j in $ сначала находим произвольные ФСР $$ lambda_3=1 Rightarrow left<begin x_1&-x_2 & &-x_4 & & & &+x_8 & =0 \ & x_2 &-x_3 & +x_4 & & -x_6 & & & =0 \ & & x_3 & +x_4 & & & -x_7 &-x_8& =0 \ & & & 3,x_4 &+x_5 & -x_6 & -2,x_7 & -x_8 & =0 \ & & & & x_5 & -x_6 & +x_7 & -x_8 & =0 end right. $$ $$ Rightarrow mathfrak X_ =left[1,1,0,0,1,1,0,0 right]^ ;mathfrak X_ =left[ 0,-1,0,1,-1,0,1,0 right]^; mathfrak X_ =left[0,1,1,0,1,0,0,1 right]^ . $$ $$ lambda_4=-1 Rightarrow quad left< begin mathfrak X_ =left[-1,1,0,0,-1,1,0,0 right]^\ mathfrak X_ =left[ 0,1,-1,0,-1,0,0,1 right]^ \ mathfrak X_ =left[0,1,0,-1,-1,0,1,0 right]^ end right>, . $$ Применяем к каждой из них алгоритм ортогонализации Грама-Шмидта: $$mathfrak Y_=mathfrak X_=left[1,1,0,0,1,1,0,0 right]^; $$ $$ mathfrak Y_=mathfrak X_+ <coloralpha > mathfrak Y_, quad langle mathfrak Y_,mathfrak Y_ rangle =0 quad Rightarrow <coloralpha >=-frac<langle mathfrak X_,mathfrak Y_ rangle><langle mathfrak Y_,mathfrak Y_ rangle >=frac quad Rightarrow $$ $$ Rightarrow mathfrak Y_=left[frac,-frac,0,1,-frac,frac,1,0 right]^ ; $$ $$ mathfrak Y_=mathfrak X_+ <colorbeta > mathfrak Y_+ <colorgamma > mathfrak Y_, quad langle mathfrak Y_,mathfrak Y_ rangle =0, langle mathfrak Y_,mathfrak Y_ rangle =0 quad Rightarrow $$ $$ <colorbeta > =-frac<langle mathfrak X_,mathfrak Y_ rangle><langle mathfrak Y_,mathfrak Y_ rangle>=-frac, <colorgamma > =-frac<langle mathfrak X_,mathfrak Y_ rangle ><langle mathfrak Y_,mathfrak Y_ rangle >=frac quad Rightarrow $$ $$ Rightarrow mathfrak Y_=left[-frac,frac,1,frac,frac,-frac,frac,1 right]^ , . $$ $$ mathfrak Y_=mathfrak X_=left[-1,1,0,0,-1,1,0,0 right]^, mathfrak Y_=left[frac,frac,-1,0,-frac,-frac,0,1 right]^, $$ $$ mathfrak Y_=left[frac,frac,frac,-1,-frac,-frac,1,-frac right]^ , . $$ После нормирования, составляем из этих векторов ортогональную матрицу: $$ P= left(begin -sqrt/4 & sqrt/4 & 1/2 & sqrt/6 & -sqrt/12 & -1/2 & sqrt/6 & sqrt/12 \ -sqrt/4 & -sqrt/4 & 1/2 & -sqrt/6 & sqrt/12 & 1/2 & sqrt/6 & sqrt/12 \ -sqrt/4 & sqrt/4 & 0 & 0 & sqrt/4 & 0 & -sqrt/3 & sqrt/12 \ -sqrt/4 & -sqrt/4 & 0 & sqrt/3 & sqrt/12 & 0 & 0 & -sqrt/4 \ sqrt/4 & -sqrt/4 & 1/2 & -sqrt/6 & sqrt/12 & -1/2 & -sqrt/6 & -sqrt/12 \ sqrt/4 & sqrt/4 & 1/2 & sqrt/6 & -sqrt/12 & 1/2 & -sqrt/6 & -sqrt/12 \ sqrt/4 & -sqrt/4 & 0 & sqrt/3 & sqrt/12 & 0 & 0 & sqrt/4 \ sqrt/4 & sqrt/4 & 0 & 0 & sqrt/4 & 0 & sqrt/3 & -sqrt/12 end right) , . $$ $$ P^AP= left( begin 3&&&&&&& \ &-3&&&&&& \ &&1&&&&& \ &&&1&&&& \ &&&&1&&& \ &&&&&-1&& \ &&&&&&-1& \ &&&&&&&-1 end right) , . $$ ♦

Видео:7 4 Собственные векторы и собственные значенияСкачать

Квадратичная форма

Экстремальное свойство собственных чисел

Пусть уравнение $ X^<^>A X=1 $ задает эллипсоид в $ mathbb R^3 $, т.е. квадратичная форма положительно определена. Построить посылочный ящик минимального объема (минимальный параллелепипед), содержащий данный эллипсоид.

Решение. Если уравнение эллипсоида приведено к каноническому виду $$ frac+frac+frac=1, $$ то ответ геометрически очевиден: эллипсоид «шире всего» в направлении оси, соответствующей максимальному из трех чисел $ a,b,c $, и «уже всего» в направлении оси, соответствующей минимальному из этих чисел. То есть размер оптимального посылочного ящика — $ (2,a, 2,b, 2,c) $. В случае, если уравнение $ X^<^>A X=1 $ не приведено к каноническому виду, его можно привести к нему с помощью ортогональной замены переменных. Такая замена оставляет инвариантными размеры эллипсоида, а результатом ее становится уравнение эллипсоида в каноническом виде $$ lambda_1 y_1^2+lambda_2 y_2^2+lambda_3 y_3^2=1 , . $$ Здесь $ lambda_1,lambda_2,lambda_3 $ — собственные числа матрицы $ A $, они являются положительными ввиду предположения о положительной определенности этой матрицы. Соответствующие собственные векторы матрицы определяют главные оси эллипсоида 1) . Сравнивая два канонических вида уравнения эллипсоида, можем размеры посылочного ящика сформулировать в терминах собственных чисел матрицы: максимальный размер эллипсоид имеет равным $ 2/sqrt<min > $, а минимальный — равным $ 2/sqrt<max > $. Если эллипсоид нельзя поворачивать вокруг начала координат, то для того, чтобы поместить его в ящик размеров $ 2/sqrt, 2/sqrt, 2/sqrt $ последний надо ориентировать в пространстве: рёбра должны быть параллельны собственным векторам матрицы $ A $. ♦

Замеченное свойство собственных чисел симметричной матрицы распространяется и в многомерное пространство. Традиционно его формулируют в несколько ином виде — хотя и менее наглядном, но более ориентированном на приложения в задачах механики и статистики.

Задача. Найти условные экстремумы квадратичной формы $ F(X)=X^<^>A X $ на единичной сфере $$ mathbb S= , . $$

В курсе математического анализа показывается, что, во-первых, указанные экстремумы существуют 2) , и, во-вторых, могут быть найдены применением метода множителей Лагранжа.

Теорема. Если $ lambda_ $ — максимальное, а $ lambda_ $ — минимальное собственные числа матрицы $ A $, то

$$ max_ X^<^>A X =lambda_, qquad min_ X^<^>A X =lambda_ , . $$ Указанные экстремумы квадратичная форма достигает на соответствующих собственных векторах матрицы $ A $ единичной длины.

Доказательство. Применяем метод множителей Лагранжа, т.е. составляем функцию $$L(X,lambda) = F(X)- lambda (X^X-1)$$ и ищем ее абсолютные экстремумы (как функции $ (n+1) $-го аргумента). На основании теоремы о стационарных точках полинома эти экстремумы должны достигаться на вещественных решениях системы уравнений $$ left< begin big/=&2left(a_x_1+a_x_2+dots+a_x_n right)-2 lambda x_1 &=0, \ dots & & dots \ big/=&2left(a_x_1+a_x_2+dots+a_x_n right)-2 lambda x_n &=0, \ big/=&x_1^2+dots +x_n^2-1 &= 0 , . end right. $$ Решаем эту систему. Первые $ n $ уравнений перепишем в матричном виде $$AX-lambda X=mathbb O iff (A-lambda , E) X=mathbb O , . $$ Из последнего уравнения системы следует, что $ X ne mathbb O $. Следовательно, решениями системы будут исключительно только собственные векторы $ _j $ матрицы $ A $, при $ lambda $ равном соответствующему собственному числу $ lambda_j $ этой матрицы. При $ X=_j $ и $ lambda=lambda_j $ получаем экстремальные значения функции $ F(X) $: $$F(_j)=_j^<^>A _j = lambda_j _j^<^>_j=lambda_j , . $$ Откуда и следует утверждение теоремы. ♦

Еще один вариант экстремального свойства симметричной матрицы излагается ☞ ЗДЕСЬ.

Видео:Собственные значения и собственные векторы. ТемаСкачать

Собственные числа и собственные векторы матрицы

Определение 9.3. Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: Ах= λх, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называетсясобственным числом матрицы А.

Подставив в формулы (9.3) x`_j = λx_j, получим систему уравнений для определения координат собственного вектора:

.

. (9.5)

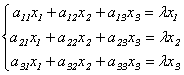
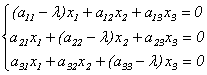
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:

получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:

поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A — λE| называется характеристическим многочленом матрицы А.

Свойства характеристического многочлена:

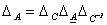
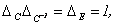
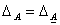
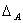
1) Характеристический многочлен линейного преобразования не зависит от выбора базиса. Доказательство. (см. (9.4)), но следовательно, . Таким образом, не зависит от выбора базиса. Значит, и |A-λE| не изменяется при переходе к новому базису.

2) Если матрица А линейного преобразования является симметрической (т.е. а_ij=a_ji), то все корни характеристического уравнения (9.6) – действительные числа.

Свойства собственных чисел и собственных векторов:

1) Если выбрать базис из собственных векторов х₁, х₂, х₃, соответствующих собственным значениям λ₁, λ₂, λ₃ матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:

(9.7) Доказательство этого свойства следует из определения собственных векторов.

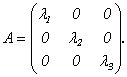
2) Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.

3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.

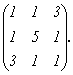
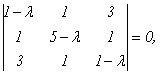
Найдем собственные числа и собственные векторы матрицы Составим характеристическое уравнение: (1- λ)(5 — λ)(1 — λ) + 6 — 9(5 — λ) — (1 — λ) — (1 — λ) = 0, λ³ — 7λ² + 36 = 0, λ₁ = -2, λ₂ = 3, λ₃ = 6.

Найдем координаты собственных векторов, соответствующих каждому найденному значению λ. Из (9.5) следует, что если х₍₁₎=<x₁,x₂,x₃> – собственный вектор, соответствующий λ₁=-2, то

— совместная, но неопределенная система. Ее решение можно записать в виде х₍₁₎=<a,0,-a>, где а – любое число. В частности, если потребовать, чтобы |x₍₁₎|=1, х₍₁₎=

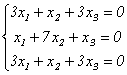
Подставив в систему (9.5) λ₂=3, получим систему для определения координат второго собственного вектора — x₍₂₎=<y₁,y₂,y₃>:

, откуда х₍₂₎=<b,-b,b> или, при условии |x₍₂₎|=1, x₍₂₎=

, x₍₃₎=<c,2c,c> или в нормированном варианте

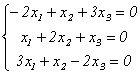
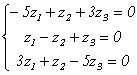
х₍₃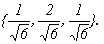₎ = Можно заметить, что х₍₁₎х₍₂₎ = ab – ab = 0, x₍₁₎x₍₃₎ = ac – ac = 0, x₍₂₎x₍₃₎ = bc — 2bc + bc = 0. Таким образом, собственные векторы этой матрицы попарно ортогональны.

Лекция 10.

Квадратичные формы и их связь с симметричными матрицами. Свойства собственных векторов и собственных чисел симметричной матрицы. Приведение квадратичной формы к каноническому виду.

Определение 10.1. Квадратичной формой действительных переменных х₁, х₂,…,х_n называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.

Примеры квадратичных форм:

(n = 2),

(n = 3). (10.1)

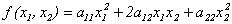
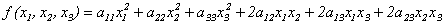
Напомним данное в прошлой лекции определение симметрической матрицы:

Определение 10.2. Квадратная матрица называется симметрической, если 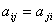, то есть если равны элементы матрицы, симметричные относительно главной диагонали.

Свойства собственных чисел и собственных векторов симметрической матрицы:

1) Все собственные числа симметрической матрицы действительные.

Доказательство (для n = 2).

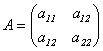
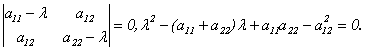
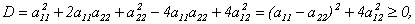
Пусть матрица А имеет вид: . Составим характеристическое уравнение:

(10.2) Найдем дискриминант:

следовательно, уравнение имеет только действительные корни.

2) Собственные векторы симметрической матрицы ортогональны.

Доказательство (для n = 2).

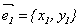
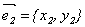
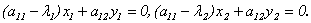
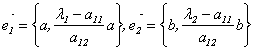
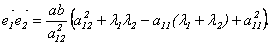
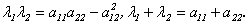
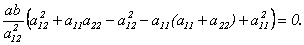
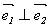
Координаты собственных векторов и должны удовлетворять уравнениям:

Следовательно, их можно задать так:

. Скалярное произведение этих векторов имеет вид:

По теореме Виета из уравнения (10.2) получим, что Подставим эти соотношения в предыдущее равенство: Значит, .

Замечание. В примере, рассмотренном в лекции 9, были найдены собственные векторы симметрической матрицы и обращено внимание на то, что они оказались попарно ортогональными.

Определение 10.3. Матрицей квадратичной формы(10.1) называется симметрическая матрица 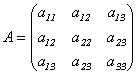. (10.3)

Таким образом, все собственные числа матрицы квадратичной формы действительны, а все собственные векторы ортогональны. Если все собственные числа различны, то из трех нормированных собственных векторов матрицы (10.3) можно построить базис в трехмерном пространстве. В этом базисе квадратичная форма будет иметь особый вид, не содержащий произведений переменных.

Видео:Симметричные и кососимметричные матрицыСкачать

О ПРИБЛИЖЕННЫХ МЕТОДАХ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ

Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Метод вращений (метод Якоби)

Для симметричной матрицы А при отыскании собственных значений и собственных векторов в настоящее время наиболее употребительным является метод вращений (метод Якоби). При его обосновании исходят из того, что определение собственных значений и собственных векторов симметричной матрицы А равносильно построению диагональной матрицы Л и ортогональной матрицы Т, связанных соотношением (см. разд. 8.9)

Диагональные элементы матрицы Л будут искомыми собственными значениями, а столбцы матрицы Т — столбцами координат собственных векторов, соответствующих этим собственным значениям. При приближенном вычислении матриц Ли Т строят последовательность матриц

где Tij — матрицы простых вращений. Матрица Д. равна произведению всех матриц Т^, примененных при построении матриц Ло, А, А2, . Ak, причем матрицы в этом произведении перемножаются слева направо в том порядке, в каком они применялись. На к-м шаге принимают Л

Матрицу в формуле (11.2) строят следующим образом. В матрице Ak выбирают наибольший по модулю недиагональный элемент

и строят матрицу простого вращения выбирая угол +1 ^ матрицы Ak+i будет иметь вид:

Из равенства нулю этого выражения получаем

Чтобы записать матриц>’’ Tjj, нужно знать cos Пример 11.1. Методом вращений найти собственные значения и собственные векторы матрицы

Р е ш е н и е. Положим Ао = А и будем строить при к = 0 но формулам (11.2) матрицы А и Т. Так как max |а^| = |«23 I = 4, то г = 2, 3 = 3 и

Угол f определяем по формуле (11.4):

Бесконечное значение тангенса указывает на то, что угол равен — Следовательно, ср — Отсюда находим cos = 1//2, — siny> = —1/л/2 и

По первой формуле (11.2) вычисляем матрицу

Следовательно, Т = То Т23 = Т23.

По тем же формулам (11.2) при к = 1 строим матрицы А2 и Т?. Для элементов матрицы А имеем: max |а-^| = | = 4//2. Поэтому

(поскольку а[g (а^ — ^ (17 — 10) -1 = ТЛТ , которое определяется ортогональной трансформирующей матрицей. ?

Метод Якоби применяют в случае произвольной действительной, а также в случае комплексной матрицы (см. [14, 29]). Если А — комплексная матрица, то вместо матрицы (11.3) простого вращения применяют унитарную матрицу

Напомним, что по формуле Эйлера

Для эрмитовой матрицы А метод Якоби остается таким же, как и в случае действительной симметричной матрицы, а именно, для максимального уменьшения на к-м шаге (см. [14]) суммы квадратов модулей недиагональных элементов матрицы /Ц номера г и j выбирают так, чтобы элемент был наибольшим по модулю недиагональным элементом матрицы Ak, а углы ф и р находят из соотношений

Возможны и различные модификации этого метода. Например, применяют метод Якоби с циклическим перебором недиагональных элементов (см. [29]).

Пример 11.2. Методом Якоби найти собственные значения и собственные векторы эрмитовой матрицы

Решение. Положим Aq = А и построим матрицы и А. Для этого замечаем, что тах|а^| = |а.121- Поэтому принимаем i — 1, j — 2. Поскольку

то гр = argai2 = — тг/2. Далее находим

📸 Видео

Решение задачи "Симметричная ли матрица"Скачать

4.5 Симметричная матрица. "Поколение Python": курс для продвинутых. Курс StepikСкачать

Собственные векторы и собственные числа линейного оператораСкачать

Собственные значения матрицыСкачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

Собственные векторы и собственные значенияСкачать

Свойства симметричной матрицы (самосопряженные линейные операторы)Скачать

Собственные числа, собственные, присоединенные векторы. Матрица оператора в базисе...Скачать

Практика 1. Часть 1. Собственные вектора и значения линейного оператора. Канонический вид.Скачать

Собственные значения и собственные векторы. ПримерСкачать