Построй четырехугольник ABCD, у которого два угла острые, а два тупые. А теперь построй четырехугольник MNPK, у которого один угол прямой, один тупой и два острых. Проверь правильность построения с помощью чертежного угольника.
Решение
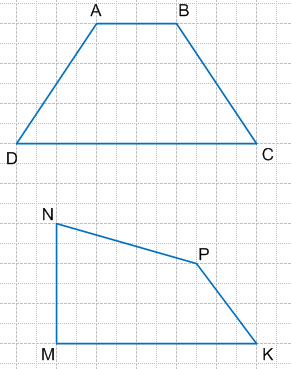
четырехугольник ABCD:
острые углы : ∠D, ∠C;
тупые углы : ∠A, ∠B.
четырехугольник MNPK:
прямой угол : ∠M;
острые углы : ∠N, ∠K;
тупой угол : ∠P.
Видео:Математика 2 класс (Урок№33 - Угол. Виды углов: прямой, острый, тупой.)Скачать

math4school.ru
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Четырёхугольники
Видео:2 класс. Математика. УглыСкачать
Основные определения и свойства

Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
Сумма углов выпуклого четырёхугольника равна 360°:
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов:
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон:
Площадь произвольного выпуклого четырёхугольника равна:

Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины.
Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет.
Площадь произвольного выпуклого четырёхугольника:



Если M , N , P , Q – середины сторон выпуклого четырёхугольника ABCD , а R , S – середины его диагоналей, то четырёхугольники MNPQ , MRPS , NSQR являются параллелограммами и называются параллелограммами Вариньона.
Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD . Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны;

Отрезки MP , NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника.
В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки.
Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам:
MG=GP , NG=GQ , RG=GS .
Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей:
MP 2 + NQ 2 + RS 2 = ¼ (AB 2 +BC 2 +CD 2 +AD 2 +AC 2 +BD 2 ).
Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь:

Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости.
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Описанные четырёхугольники

Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной.
Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны:
Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно:
Площадь описанного четырёхугольника:
где r – радиус вписанной окружности, p – полупериметр четырёхугольника.
Площадь описанного четырёхугольника:

Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника:
AK = AN , BK = BL , CL = CM , DM = DN .
Если O – центр окружности, вписанной в четырёхугольник ABCD, то
∠AOB+∠COD = ∠BOC+∠AOD =180°.
Для описанного четырёхугольника ABCD со сторонами AB = a , BC = b , CD = c и AD = d верны соотношения:
Видео:Угол Виды углов | Математика 2 класс #24 | ИнфоурокСкачать

Вписанные четырёхугольники

Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника.
Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°:
Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Радиус окружности, описанной около четырёхугольника:
Площадь вписанного четырёхугольника:

Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами.
Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов.
У вписанного четырёхугольника любые два связанных угла равны.

Если четырёхугольник одновременно является описанным и вписанным, то его площадь:
Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение:
Видео:Виды угловСкачать

Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:
У параллелограмма противолежащие стороны равны и противолежащие углы равны:
Сумма любых двух соседних углов параллелограмма равна 180°:
∠A +∠ B =∠ B +∠ C =∠ C +∠ D =∠ A +∠ D =180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:
Каждая диагональ делит параллелограмм на два равных треугольника:
∠ ABC =∠ CDA ; ∠ ABD =∠ CDB .
Две диагонали параллелограмма делят его на четыре равновеликих треугольника:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
e 2 +f 2 = a 2 +b 2 +a 2 +b 2 = 2(a 2 +b 2 ).
- Если у четырёхугольника противолежащие стороны попарно равны, то этот четырёхугольник – параллелограмм.
- Если у четырёхугольника две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
- Четырёхугольник, диагонали которого в точке пересечения делятся пополам – параллелограмм.
- Если у четырёхугольника противолежащие углы попарно равны, то этот четырёхугольник – параллелограмм.

Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне:
Площадь параллелограмма можно определить:
- через его сторону и высоту, проведённую к ней:
- через две его стороны и угол между ними:

Ромбом называется параллелограмм, у которого все стороны равны:
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:
∠ ABD =∠ CBD =∠ ADB =∠ CDB ; ∠ BAC =∠ DAC =∠ BCA =∠ DCA .

В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей.
Радиус окружности, вписанной в ромб, можно вычислить:
- через диагонали ромба и сторону:
- через отрезки, на которые делит сторону ромба точка касания:
Площадь ромба можно определить:
- через сторону и угол ромба:
- через сторону и радиус вписанной окружности:
Видео:Математика 2 класс (Урок№36 - Прямоугольник.)Скачать

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые:

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка:
Площадь прямоугольника можно определить:
- через диагонали и угол между ними:

Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали:
Видео:Страница 10 Задание 4 – Математика 2 класс Моро М.И. – Учебник Часть 2Скачать

Квадрат

Квадрат – это прямоугольник, у которого все стороны равны:

Диагонали квадрата равны и перпендикулярны.
Сторона и диагональ квадрата связаны соотношениями:

У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.
Радиус описанной окружности:
Радиус вписанной окружности:
Видео:Математика. 2 класс. Виды углов. Многоугольники /11.01.2021/Скачать

Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:
Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.

Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции:
Средняя линия трапеции параллельна её основаниям и равна их полусумме:

При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ:
Δ AED ∼ Δ BEC , k = AD / BC .
Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ:
Δ AОD ∼ Δ CОВ , k = AD / BC .
Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны:

Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон:
Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон:
Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств:
Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом:
Радиус вписанной в трапецию окружности можно определить:
- через отрезки, на которые делится боковая сторона точкой касания:

Равнобокой называется трапеция, у которой боковые стороны равны:
У равнобокой трапеции:
- углы при основании равны:
- сумма противолежащих углов равна 180?:
Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Стороны и диагональ равнобокой трапеции связаны соотношением:

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

Площадь трапеции можно определить:
- через полусумму оснований (первую среднюю линию) и высоту:
- через диагонали и угол между ними:
Видео:Математика. Углы прямые, острые, тупые.Скачать

Дельтоид


Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон.
Дельтоид может быть выпуклым или невыпуклым.
Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом.
В любом дельтоиде углы между соседними неравными сторонами равны.
Площадь любого дельтоида можно определить:
- через две соседние неравные стороны и угол между ними:


В любой выпуклый дельтоид можно вписать окружность.
Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида.
Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины.

Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°.
Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
Видео:Математика 2 класс. "Виды углов. Многоугольники"Скачать
Ортодиагональные четырёхугольники

Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом.
Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
- для сторон четырёхугольника верно: a²+c² = b²+d ²;
- для площади четырёхугольника верно: S = ½ef ;
- параллелограмм Вариньона с вершинами в серединах сторон четырёхугольника является прямоугольником.

Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности:

Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны:
Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О , то верны соотношения:
Видео:Страница 10 Задание 4 – Математика 2 класс (Моро) Часть 2Скачать

Четырехугольник 2 угла острых и 2 тупых
Вопрос по математике:
Построить четырехугольник ABCD, у которого два угла острые, а два — тупые. А теперь построить четырехугольник MNPK, у которого один угол прямой, один тупой и два острых.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Вот смотри, возможно так будет выглядить первый четырехугольник. Двумя дугами это тупые углы, одной — острые.
Вот второе. Не уверена, что верно, но впринципе, по условию сходится
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
🌟 Видео
Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

3 правила для вписанного четырехугольника #shortsСкачать

Математика. 2 класс. Виды многоугольников. Свойства квадрата и прямоугольника /12.01.2021/Скачать

11 класс, 44 урок, Описанный четырехугольникСкачать

1 задание. Четырехугольник 2 ЧАСТЬ - ГОДОВОЙ КУРС ПРОФИЛЬ ЕГЭ 2023 Абель / Математика ЕГЭСкачать

Математика 29. Четырехугольники, прямоугольник, квадрат — Шишкина школаСкачать




































