Чем вектор отличается от точки

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Геометрия 9 Откладывание вектора от данной точкиСкачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Что такое вектор

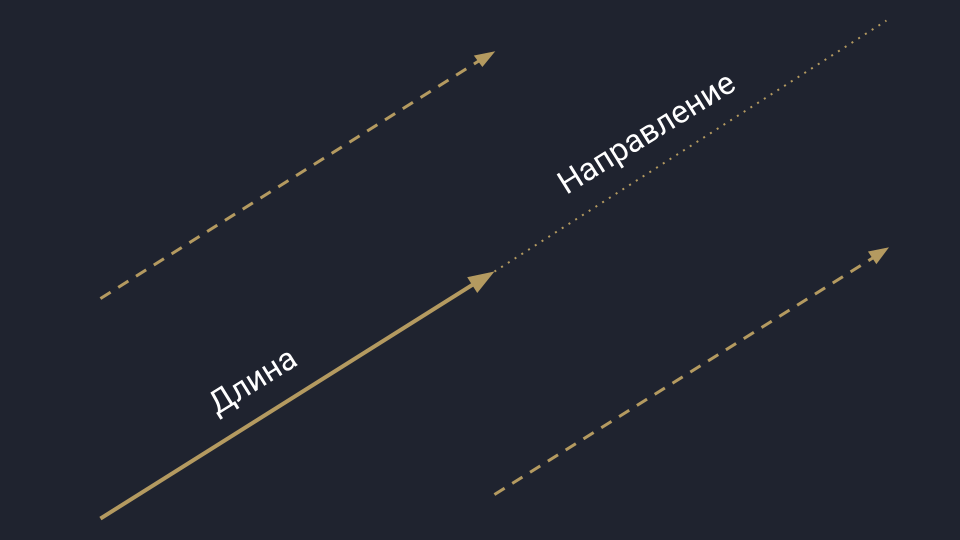
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

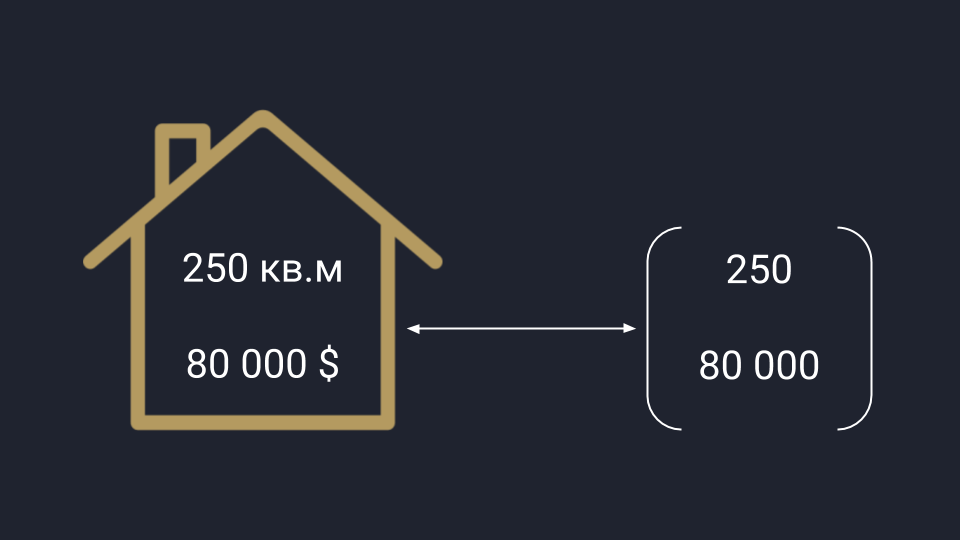
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

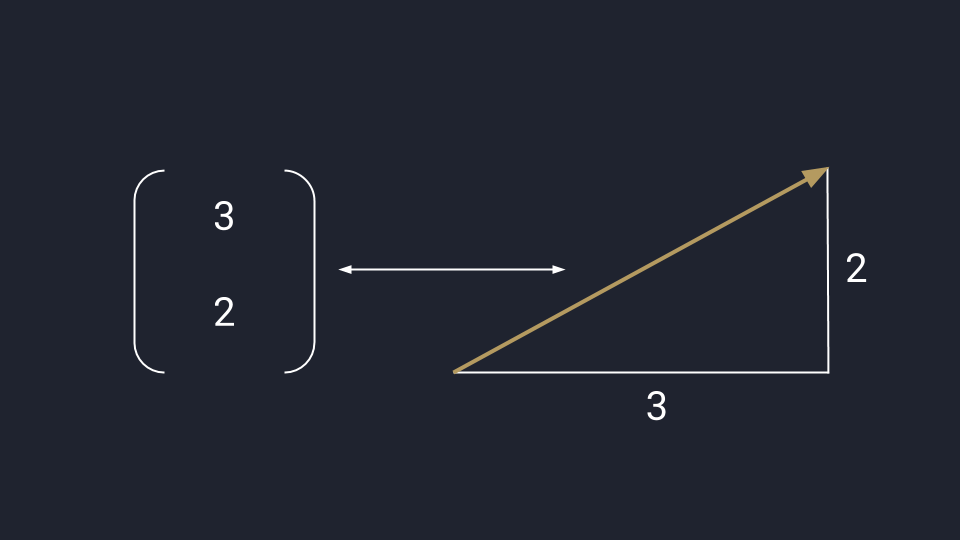
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

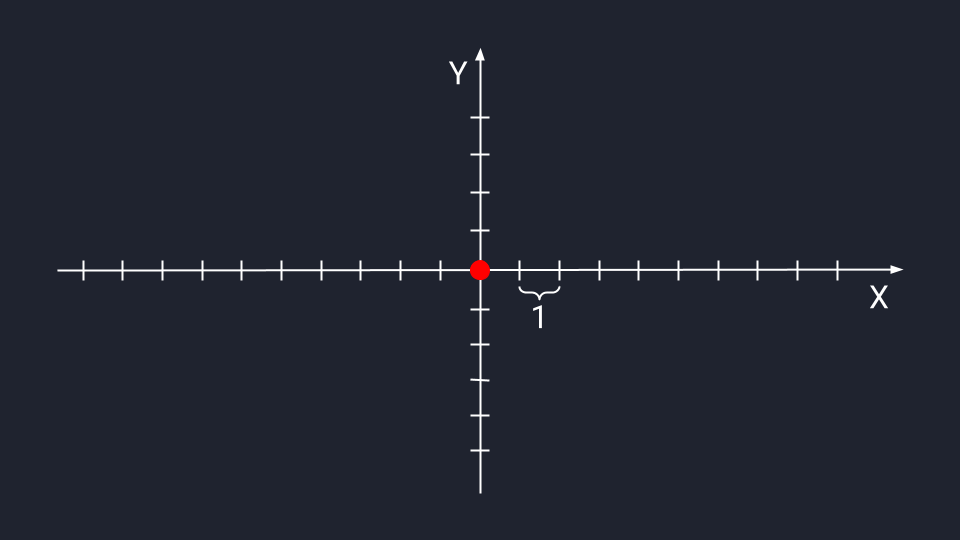
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:8 класс, 42 урок, Откладывание вектора от данной точкиСкачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

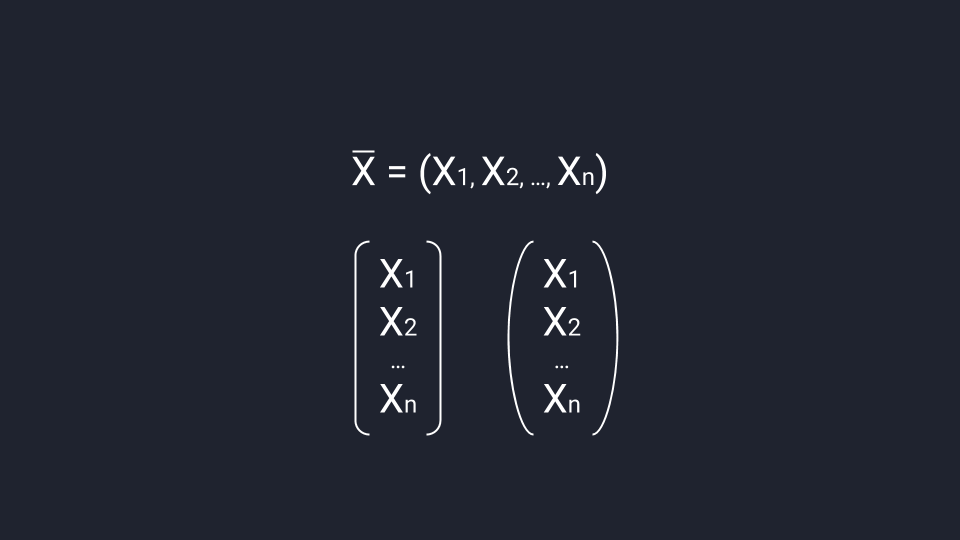
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Как изображать

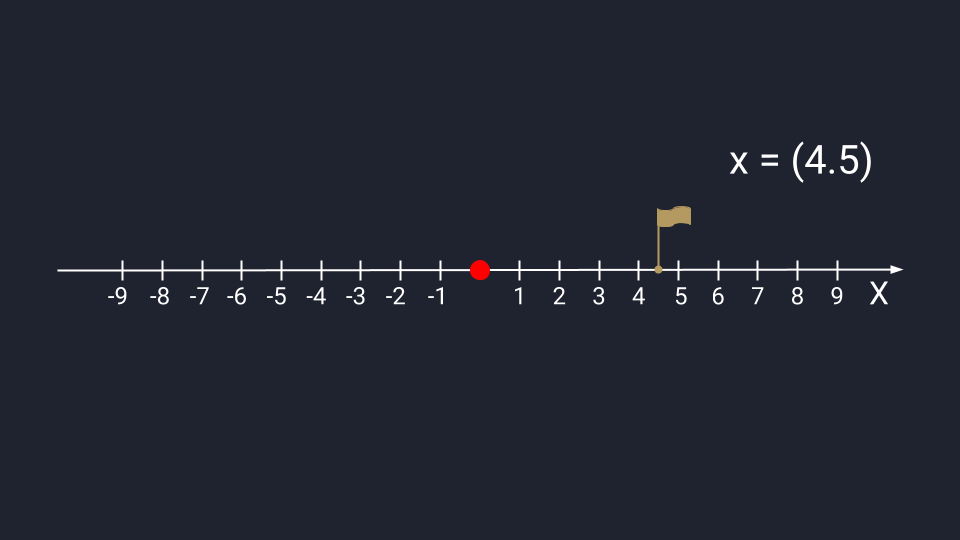
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

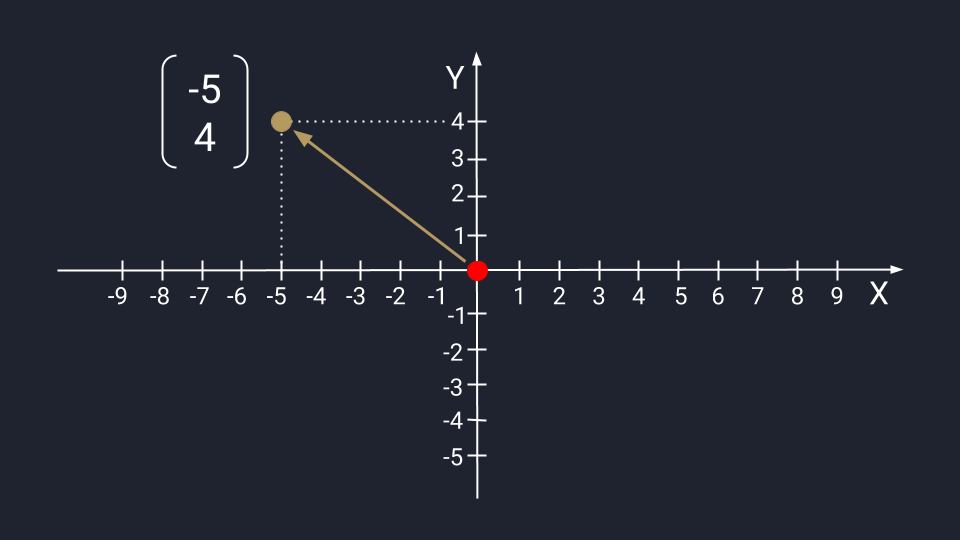
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

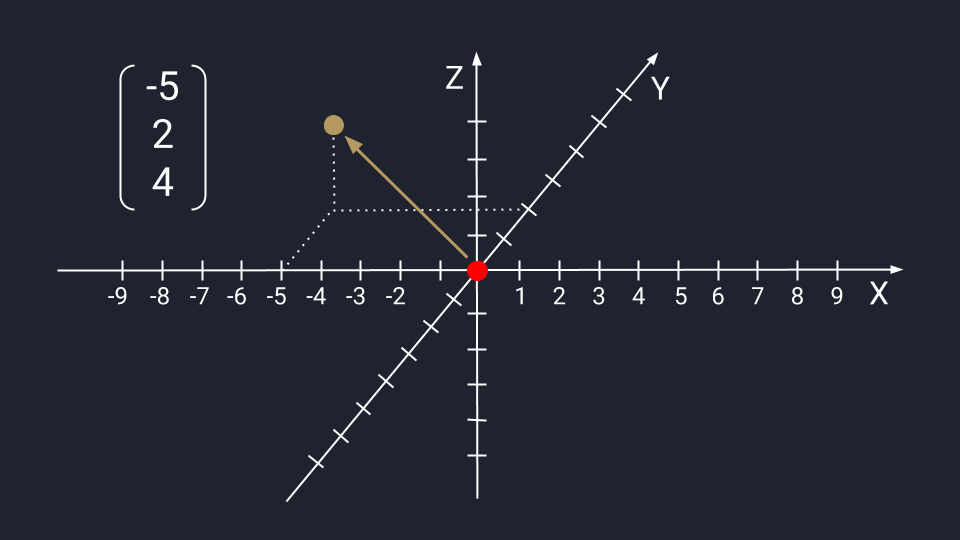
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

Видео:81. Откладывание вектора от данной точкиСкачать

В чем разница между точкой и вектором?

Я понимаю, что вектор имеет направление и величину, а точка — нет.

Однако в курсах, которые я использую, указано, что точка совпадает с вектором.

Кроме того, можете ли вы сделать продукт с несколькими продуктами и точками вместо двух векторов? Я так не думаю, но мой сосед по комнате настаивает, да, и сейчас я немного смущен.

Вот ответ без использования символов.

Разница заключается именно в том, что между location и смещением .

• Точки местоположения в пространстве .
• Векторы перемещаются в пространстве .

Аналогия со временем работает хорошо.

• Времена (также называемые моментами или датами) местоположения во времени .
• Длительность смещения во времени .

Итак, со временем,

• 4:00 p.m., noon, midnight, 12:20, 23:11, etc. are times
• +3 hours, -2.5 hours, +17 seconds, etc., are durations

Обратите внимание, как длительность может быть положительной или отрицательной; это дает им «направление» в дополнение к их чисто скалярному значению. Теперь лучший способ мысленно различать время и продолжительность — это операции, которые они поддерживают

• С учетом времени вы можете добавить продолжительность, чтобы получить новое время (3:00 + 2 часа = 5:00).
• Вы можете вычесть два раза, чтобы получить продолжительность (7:00 — 1:00 = 6 часов).
• Вы можете добавить две длительности (3 часа, 20 минут + 6 часов, 50 минут = 10 часов, 10 минут).

Но вы не можете добавить два раза (3:15 am.m + noon = . )

Давайте проведем аналогию, чтобы теперь говорить о космосе:

• $(3,5)$, $(-2.25,7)$, $(0,-1)$, etc. are points
• $langle 4,-5 rangle$ is a vector, meaning 4 units east then 5 south, assuming north is up (sorry residents of southern hemisphere)

Теперь у нас есть те же аналогичные операции в пространстве, что и мы со временем:

• Вы можете добавить точку и вектор: начиная с $ (4,5) $ и переходя $ langle -1,3 rangle $ переводит вас в точку $ (3,8) $
• Вы можете вычесть две точки, чтобы получить смещение между ними: $ (10,10) — (3,1) = langle 7,9 rangle $, что является смещением, которое вы могли бы взять со второго места, чтобы получить к первому
• Вы можете добавить два смещения, чтобы получить сложное смещение: $ langle 1,3 rangle + langle -5,8 rangle = langle -4,11 rangle $. То есть, идя на 1 шаг на север и на 3 востока, ТОГДА идет 5 юг и 8 восток — это одно и то же и только 4 юга и 11 востока.

Но вы не можете добавить две точки.

Более конкретно: Москва + $ langle text rangle $ — другое место (точка) где-то на земле. Но Москва + Лос-Анджелес не имеет смысла.

Подводя итог, укажите, где (или когда) вы находитесь, а смещение — , как добраться из одного места в другое. . Перемещения имеют как величину (как далеко продвинуться), так и направление (которое во времени одномерное пространство просто положительно или отрицательно). В пространстве местоположения расположены точки , а смещения — векторы . Со временем местоположения (время в секундах), a.k.a. моментов , а смещения — продолжительности .

EDIT 1: In response to some of the comments, I should point out that 4:00 p.m. is NOT a displacement, but «+4 hours» and «-7 hours» are. Sure you can get to 4:00 p.m. (an instant) by adding the displacement «+16 hours» to the instant midnight. You can also get to 4:00 p.m. by adding the diplacement «-3 hours» to 7:00 p.m. The source of the confusion between locations and displacements is that people mentally work in coordinate systems relative to some origin (whether $(0,0)$ or «midnight» or similar) and both of these concepts are represented as coordinates. I guess that was the point of the question.

EDIT 2: I added some text to make clear that durations actually have direction; I had written both -2.5 hours and +3 hours earlier, but some might have missed that the negative encapsulated a direction, and felt that a duration is «only a scalar» when in fact the adding of a $+$ or $-$ really does give it direction.

Точки и векторы — это не одно и то же. Учитывая две точки в трехмерном пространстве, мы можем сделать вектор от первой точки до второй. И, учитывая вектор и точку, мы можем начать с точки и «следовать» вектору, чтобы получить другую точку.

Однако есть приятный факт: точки в трехмерном пространстве (или $ mathbb ^ n $, в более общем плане) находятся в очень хорошем соответствии с векторами, начинающимися в точке $ (0,0,0) $. По сути, идея состоит в том, что мы можем представить вектор с его конечной точкой, и никакая информация не будет потеряна. Это иногда называют переносом вектора в «стандартную позицию».

Для курса, такого как векторное исчисление, важно сохранить хорошее различие между точками и векторами. Точки соответствуют векторам, начинающимся в начале координат, но нам могут понадобиться векторы, которые начинаются в других точках.

Например, учитывая три точки $ A $, $ B $ и $ C $ в трехмерном пространстве, мы можем захотеть найти уравнение плоскости, которое их охватывает. Если бы мы только знали нормальный вектор $ vec n $ плоскости, мы могли бы написать уравнение непосредственно как $ vec n cdot (x, y, z) = vec n cdot A $. Поэтому нам нужно найти нормальный $ vec n $. Для этого мы вычисляем поперечное произведение векторов $ vec $ и $ vec $. Если бы мы вычислили поперечное произведение $ A $ и $ C $ (притворяясь, что они являются векторами в стандартном положении), мы не смогли бы получить правильный нормальный вектор.

Например, если $ A = (1,0,0) $, $ B = (0,1,0) $ и $ C = (0,0,1) $, нормальный вектор соответствующей плоскости не будет параллельны любой координатной оси. Но если мы возьмем любые два из $ A $, $ B $ и $ C $ и вычислим кросс-произведение, мы получим вектор, параллельный одной из осей координат.

В духе они разные вещи. Но обычное соглашение — думать о векторе в плоскости или в трехмерном пространстве, начиная с начала координат. В этом случае вектор идентифицируется точно по его конечной точке, что дает вам идентификацию между точками и векторами.

Один из способов увидеть, что это разные вещи (даже если они идентифицированы во многих случаях), состоит в том, что вы можете добавлять векторы, а сумма баллов не имеет смысла. То же самое с точкой и кросс-продуктами.

Что такое a вектор? Вы правы, что мы обычно рассматриваем вектор как нечто, имеющее направление и величину, но более точное и абстрактное определение состоит в том, что вектор, например, в $ mathbb ^ n $, просто этого набора. Таким образом, это то же самое, что и точка, когда вы рассматриваете ее как элемент набора.

Теперь, если вы хотите поговорить о перекрестных продуктах и ​​величинах, тогда возникает вопрос о лингвистике. Как вы, например, определяете величину как функцию $$ lvert cdot rvert: mathbb ^ 2 to mathbb $$ заданные для $ a = (a_1, a_2) in mathbb ^ 2 $ на $$ lvert a rvert = sqrt . $$ Поэтому, если вы настаиваете на том, чтобы говорить о величине точки, тогда вы «свободны» для этого (т. Е. Свободно определить это). Но не забывайте, что вы также будете создавать путаницу, делая это. И, выполняя математику, мы хотим четко и ясно общаться .

Точно так же вы можете определить добавление или перекрестное произведение очков.

Может быть, было бы лучше сказать следующее: Является ли векторное пространство таким же, как набор? Да, векторное пространство — это множество. Но это также больше, чем набор. Мы не можем добавить элементы набора, но мы можем добавить элементы векторного пространства, потому что с векторным пространством вы получите определение сложения. Поэтому в этом смысле точка и вектор сильно различаются.

Added: If you want to find the equation of a plane that contains the three points $a$, $b$, and $c$, then you would not subtract the points. So how do you so it. Well, if the coordinates to point $a$ are $(a_1, a_2, a_3)$, i.e. if $a = (a_1, a_2, a_3)$, (and likewise for $b$ and $c$) then you first define the vectors $$ vec = (b_1 — a_1, b_2- a_2, b_3 — a_3) $$ and $$ vec = (c_1 — a_1, c_2- a_2, c_3 — a_3). $$ Then a normal vector for/to the plane is the cross product of the vectors: $vectimes vec$.

Это вопрос, который вызывает много путаницы, и хорошо, что вы пытаетесь очистить его как можно раньше. Это, безусловно, вопрос о геометрическом значении векторов, поэтому ИМХО это не полезно, когда люди начинают привлекать векторные пространства в дискуссии.

Позвольте мне предположить, что вы знаете, в чем дело, и что путаница начинается с введения векторов. Я не знаю, как включать диаграммы в сообщение, поэтому я должен попросить вас сделать свой собственный. Вы можете визуализировать вектор как стрелку в плоскости (или в $ 3 $ -мерном пространстве, но давайте теперь придерживаться плоскости). Обычное понимание состоит в том, что вектор определяется его длиной и направлением, а не , где он находится в плоскости. Например, нарисуйте стрелку от $ (1, -2) $ до $ (3,1) $ и другую от $ (0,2) $ до $ (2,5) $. Две стрелки имеют одинаковую длину и направление, поэтому они рассматриваются как тот же вектор и могут быть записаны как вектор $ (2,5) $ или $ 2 + 5 $, если это обозначение, которое используют ваши инструкторы.

Мы часто используем язык немного свободно и ссылаемся на точку как вектор. (Точнее сказать, что точка представлена ​​ вектором, но вопреки распространенному мнению математики не всегда на 100% точны в том, как они говорят!) В этом случае мы имеем в виду вектор от начала координат до указанной точки. Таким образом, первый вектор, нарисованный выше, не представляет точку $ (3,1) $, так как он не начинается с начала координат. С другой стороны, если вы нарисуете стрелку от $ (0,0) $ до $ (2,5) $, тогда вы увидите, что это тот же вектор (то есть, имеет ту же длину и направление), что и другой два. Поскольку он начинается с начала координат, этот вектор представляет точку $ (2,5) $ — как и другие два, поскольку они являются одним и тем же вектором. Как вы можете видеть, вектор из начала и точки, которые он представляет, является одним и тем же численно , но они различаются концептуально , и стоит потратить некоторое время, пытаясь получить голову вокруг него.

Другой пример — если вы еще этого не видели, я ожидаю, что вы скоро это сделаете. Уравнение прямой может быть записано в «параметрической векторной форме», как, например, $$ = (1,2) + lambda (3,4) quad hbox <для $ lambda in $>. $$ Здесь мы рассматриваем вектор $ (1,2) $ как указание точки на линии и $ (3,4) $ как указание направления линии. Значит, важно, чтобы мы нарисовали $ (1,2) $, начиная с начала координат (пожалуйста, нарисуйте его), но важно не , где мы рисуем $ ( 3,4) $, и самым простым способом является его начало начиная с $ (1,2) $ и переходя к $ (4,6) $. Затем вы можете провести линию через $ (1,2) $ в направлении $ (3,4) $, и это строка, указанная выше. Обозначение $ $ будет переменной точкой на линии, или, другими словами, переменным вектором от начала координат до прямой.

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Геометрия для новичков. Часть 1: координаты и векторы — теория

Внимание! Этот документ ещё не опубликован.

Видео:Откладывание вектора от данной точки | Геометрия 7-9 класс #78 | ИнфоурокСкачать

О чем данная статья

В данной статье дается теоретическое описание векторов, координат векторов и операций над ними.

Видео:Понятие вектора. Равенство векторов. Откладывание вектора от данной точкиСкачать

На кого рассчитана статья

Прежде чем читать эту статью, нужно знать:

• что такое прямоугольная система координат и координаты точки на плоскости
• что такое теорема Пифагора

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Введение

Видео:9 класс, 3 урок, Связь между координатами вектора и координатами его начала и концаСкачать

Зачем нужны координаты точек в играх

В любой игре положение игрового объекта задается координатами какой-либо точки, привязанной к этому объекту, т.е. эта точка перемещается вместе с объектом. Например, мы можем задать координаты объектов в «Супер Марио» следующим образом:

На этом рисунке крупные черные точки — это точки, привязанные к игровым объектам. Координаты этих точек мы и будем считать координатами игровых объектов.
Итак, на этом рисунке:

• координаты Марио равны (-0.5, -2)
• координаты улитки равны (3, -2)
• координаты кубика равны (4, 1)

Видео:Физика | Ликбез по векторамСкачать

Пример координат вектора

Я намеренно не написал конкретные значения для координат точек – пусть они будут произвольными.

Зададим себе вопрос «Как нужно изменить начальные координаты Марио, что получить конечные?» Чтобы ответить на этот вопрос, нам нужно найти пару чисел (x, y), таких, чтобы:

Ax + x = Bx
Ay + y = By

Решая эти 2 уравнения, получаем:

x = Bx — Ax
y = By — Ay

Пара (x, y) в нашей задаче является координатами вектора перемещения Марио. Но это — лишь конкретный пример координат вектора. Что такое вектор и что такое его координаты в общем случае? Сейчас узнаем.

Видео:Коллинеарные векторы.Скачать

Векторы

Видео:Перемещение | Физика 9 класс #2 | ИнфоурокСкачать

Что такое направленный отрезок

Стрелка показывает, что А – начало отрезка, а B – конец.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Что такое вектор

Что у этих отрезков общего? Хм, пожалуй 2 вещи:

• Направление
• Длина

Так вот, вектор – это как раз и есть совокупность направления и длины.
Направленный отрезок – не вектор, который мы изучаем в геометрии. Направленный отрезок задает, или как еще говорят, представляет вектор. Но это — не вектор.
В нашем примере направленный отрезок представляет вектор . Разницу в черточках наверху заметили? Еще часто вектор обозначают 1 буквой, например:

Примечание: о тонкостях приведенного мной определения — в конце статьи.

Видео:ОЧЕНЬ ВАЖНЫЙ УРОК. РАЗНИЦА МЕЖДУ ВЕКТОРНОЙ И РАСТРОВОЙ ГРАФИКОЙ. СРАВНИВАЕМ. ДОСТУПНО И БЕЗ ВОДЫСкачать

Равенство векторов

Если задуматься, все направленные отрезки одинаковой длины, которые лежат на параллельных прямых и указывают в одну сторону, имеют одинаковое направление и длину. Следовательно, все эти направленные отрезки представляют один и тот же вектор. Из этого следует определение равенства 2 векторов:

Два вектора и , представленные направленными отрезками и называются равными, если:

• и лежат на параллельных прямых
• и направлены в одну сторону
• и имеют одинаковую длину

Из данного определения следует, что при параллельном переносе произвольный направленный отрезок продолжает представлять тот же вектор, что он представлял до переноса. Это свойство активно используется для операций над векторами.

Видео:Координаты точки и координаты вектора 1.Скачать

Длина вектора

Видео:11 класс, 3 урок, Связь между координатами векторов и координатами точекСкачать

Коллинеарные векторы

На рисунке любая пара из векторов , , является коллинеарными векторами

Если отрезки, представляющие коллинеарные векторы, имеют одинаковое направления, то векторы называют сонаправленными:

Пишут:
Если отрезки, представляющие коллинеарные векторы, имеют противоположное направления, то векторы, представленные данными отрезками, называют противоположно направленными:

Пишут:

Видео:8 класс, 40 урок, Понятие вектораСкачать

Нулевой вектор

Единичные векторы

=1

Обратный вектор

Арифметические операции над векторами

1. Вектор можно умножать на число. Вектор , умноженный на число, записывается как k*. Вектор будет сонаправлен (противоположно направлен) с вектором , если k — положительное (отрицательное) число. Вектор k* будет иметь длину |k|*||:

|k*| = |k|*||
k* , если k>0
k* , если k 0, такое, что:
|k * |=1

Т.е. в результате нормализации мы получаем единичный вектор, сонаправленный с исходным вектором
Важно: нулевой вектор НЕЛЬЗЯ нормализовать, так как для любого числа k:

|k*| = |k|*|| = k * 0 = 0

Итак, как же найти это число k?
Распишем |k * | по определению:

|k * | = |k| * || = k * || = 1

Здесь мы убрали с k знак модуля, так как по определению k > 0.
Итак:

k * || = 1

Из этого следует, что:

k = 1 / ||

Т.е. чтобы нормализовать произвольный ненулевой вектор, нам нужно разделить вектор на его длину.

Координаты вектора

Вроде бы из примера, приведенного в начале статьи, все понятно: координаты вектора — разность координат конца и начала направленного отрезка, представляющего вектор.

Но это не так. Действительно, значения координат вектора численно равны этой разности. Но определение координат вектора в корне отличается от определения координат точки.

Разложение вектора по 2 неколлинеарным векторам

В геометрии доказывается следующий факт.

Ecли мы возьмем 2 неколлинеарных вектора и ,
то для каждого вектора можно подобрать 2 числа k и s, для которых выполняется равенство:

= k* + s*

Теперь возьмем в качестве таких неколлинеарных векторов и следующие векторы:

• вектор – направление – вдоль оси Ox, длина равна 1
• вектор – направление – вдоль оси Oy, длина равна 1

Векторы и называют координатными векторами.

Определение координат вектора

= x* + y*

то пара чисел (x, y) будет называться координатами вектора .
Часто пишут:

= (x, y)

Эта запись означает, что вектор имеет координаты x и y.

Арифметические операции над координатами векторов

— = (-ax, -ay)

Координаты вектора, умноженного на число, равны координатам исходного вектора, умноженными на это число:

k* = (k*ax, k*ay)

Пусть у нас есть 2 произвольных вектора =(ax, ay) и =(bx, by). Тогда:

1. кoординаты суммы 2 векторов равны сумме x- и y-координат векторов:
   + = (ax + bx, ay + by)
2. как следствие из предыдущих свойств, координаты разности 2 векторов равны разности координат этих векторов:
   — = (ax — bx, ay — by)

Т.е. арифметика для координат векторов – такая же, как и для обычных чисел, только все считается покоординатно.

Радиус-вектор

Можно доказать, что численные значения координат точки совпадают со значения координат ее радиус-вектора. Здесь примем это как факт:
=(Ax, Ay)
где (Ax, Ay) — координаты точки A

Связь между координатами вектора и координатами концов отрезка

если – направленный отрезок, представляющий вектор , то значения координат вектора (x, y) вычисляются по формуле:

(x, y) = (Bx — Ax, By — Ay)

где (Ax, Ay), (Bx, By) — координаты точек А и B соответственно.

Докажем это.
Мы можем записать простое равенство для произвольного вектора :

= —

Заметим, что и — радиус векторы.
Из равенства значений координат точки и радиус-вектора и предыдущей формулы следует, что:

(x, y) = (Bx — Ax, By — Ay)

Нахождение длины вектора по его координатам

Пусть у нас есть вектор , представленный отрезком . Координаты вектора равны (x, y).
Чтобы найти длину вектора через его координаты, воспользуемся теоремой Пифагора и равенством:

= +

По теореме Пифагора:

AC = || = |x|,
СB = || = |y|

то в итоге получаем равенство:

Заключение

Применению векторов в реальных задачах игровой разработки будет посвящена следующая моя статья. В ней практически не будет математики и будет много программирования.

Здесь же я описал то, что будет необходимо для понимания практических приемов использования векторов.
Если не иметь представления, как связаны координаты точек и координаты векторов, очень сложно понять, как работают алгоритмы определения расстояний от точки до геометрической фигуры, алгоритмы обнаружения столкновений и т.д.

Так что не жалейте, если вы (о ужас!) кое-что запомнили из «всей этой математики». Все это вам пригодится очень скоро, обещаю.

Литература

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. «Геометрия», 7-9 классы»
Главы: «Векторы», «Метод координат».

PS: корректность определения вектора в статье

Вся хитрость в том, что существует несколько определений вектора даже в рамках геометрии.

Направленный отрезок – тоже вектор, так называемый фиксированный вектор. Но нужно учитывать один важный факт – 2 фиксированных вектора равны тогда и только тогда, когда их концы и начала совпадают. А это не то определение равенства 2 векторов, что дает учебник геометрии.

Определение вектора, данное в этой статье – определение так называемого свободного вектора.
Каждый свободный вектор – это множество фиксированных векторов, которые имеют равную длину и одинаковое направление.

Именно это определение учебник геометрии и пытается дать в неявном виде, когда вводит понятие равенства векторов. Но здесь возникает нестыковка – учебник объясняет, как работать со свободными векторами, изначально дав определение фиксированного вектора.

Надеюсь, вышесказанное объясняет, почему я привел в данной статье «свое» определение вектора.