3 равенство треугольников задачи (2 видео)

Задачи на признак равенства треугольников: второй и третий признак

Содержание

Второй признак равенства треугольников
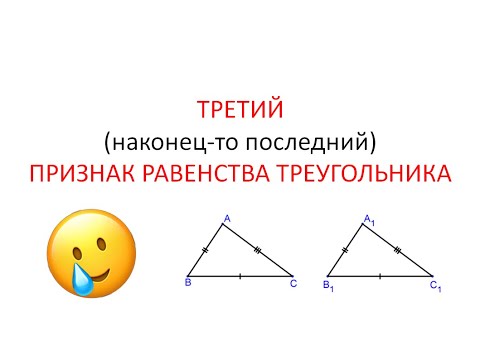
Третий признак равенства треугольников
Задачи
Задачи на третий признак равенства треугольников
3 равенство треугольников задачи
I уровень сложности (легкий)
III уровень сложности (сложный)
Самостоятельная работа № 6 Указания к решению и ОТВЕТЫ
С-6. I уровень сложности (ответы)
С-6. II уровень сложности (ответы)
С-6. III уровень сложности (ответы)
🌟 Видео

Второй признак равенства треугольников

Отсюда вытекает следующее теоремма:

Третий признак равенства треугольников

Видео:Признаки равенства треугольников. 7 класс.Скачать

Задачи

Задача 1
Дано:
ABC — равнобедренный треугольник.
АМ и BN биссектрисы угла.
Доказать: AM = BN.

Доказательство:
Треугольники AMB и BNA — равны (по второму признаку — угол-сторона-угол) потому что:
1. ∠CAB = ∠CBA
2. AB – в обеих треугольниках.
3. ∠MAB = ∠NBA = 1 /₂ ∠CAB.
Отрезки AM и BN являются соответствующими в этих равных треугольниках, и, следовательно, AM = BN.

Задача 2
Дано:
ABC — треугольник,
CM — медиана,
AA₁ ⊥ CM и BB₁ ⊥ CM.
Доказать: АА₁ = ВВ₁.

Доказательство:
1. ∠BB₁M = ∠AA₁M = 90&deg,
2. ∠AMA₁ = ∠BMB₁ как вертикальные,
3. AM = BM.
Следовательно △AA₁M = △BB₁M (по второму признаку).
Тогда AA₁ = BB₁ как соответствующие стороны в этих треугольниках.

Задача 3
Докажите, что перпендикуляры, проведённые из любой точки биссектрисы угла по отношению к его сторонам, вырезают на них равные отрезки.

Доказательство:
Давайте предположим, что ∠AOB точка M — неопределённая точка на биссектрисе OL.(fig.40)
Возьмём, что MP ⊥ OA и MQ ⊥ OB. Для того, чтобы доказать, что OP = OQ, достаточно доказать что △OPM = △OQM.

Но △OPM = △OQM(по второму признаку), потому что
1. OM — общая сторона,
2. ∠QOM = ∠POM (OL есть биссектриса),
3. ∠OQM = ∠OPM = 90°, откуда OP = OQ

Задача 4
Докажите, что если в треугольнике высота и биссектриса, проведенные из одной вершины, равны, то треугольник равнобедренный.

Доказательство:
Обозначим, что △ABC высота и биссектриса, проведённые из вершины C, совпадают (рис. 41).
Для того, чтобы доказать, что AC = BC, т.е. △ABC является равнобедренным, достаточно доказать, что △APC = △ BPC.
Но △APC = △BPC (по второму признаку) потому что
1. ∠ACP = ∠BCP (CP — биссектриса)
2. ∠ACP = ∠CPB = 90° (CP — высота)
3. CP — общая сторона
Следователвно AC = BC ⇒ ABC — равнобедренный

Задача 5

Давайте посмотрим на треугольники △ABC и △A₁B₁C₁
1. AB = A₁B₁
2. BC = B₁C₁
3. ABC = A₁B₁C₁
Тогда, △ABC = △A₁B₁C₁ — равны по первому признаку.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

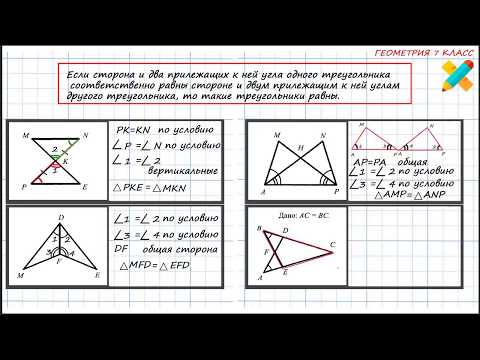
Задачи на третий признак равенства треугольников

Рассмотрим задачи на третий признак равенства треугольников.

Дано:

Рассмотрим треугольники AFB и BKA.

1) AF=BK (по условию).

2) AK=BF (по условию).

3) AB — общая сторона.

Следовательно, ∆AFB=∆BKA по третьему признаку равенства треугольников (по трем сторонам).

Что и требовалось доказать.

Дано:

Равенство углов следует из равенства треугольников. Значит, чтобы доказать равенство углов A и C, надо доказать равенство треугольников с углами A и C. Треугольников пока нет, поэтому необходимо дополнительное построение.

Проведем отрезок BD и рассмотрим треугольники ABD и CDB.

(Важно правильно назвать треугольники!

Равные углы должны стоять в названии треугольников на одинаковых местах).

Для удобства выделим треугольники разными цветами.

∆ABD и ∆CDB имеют по две пары равных сторон: AB=CD, AD=BC.

Сторона BD — общая. Можем применить третий признак равенства треугольников.

Перейдем к записи доказательства.

Проведем отрезок BD.

Рассмотрим ∆ABD и ∆CDB.

1) AB=CD (по условию).

2) AD=BC (по условию).

3) BD — общая сторона.

Следовательно, ∆ABD = ∆CDB (по трем сторонам).

Из равенства треугольников следует равенство соответствующих углов. Значит, ∠A=∠C.

Видео:Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

3 равенство треугольников задачи

Основная дидактическая цель урока: совершенствовать навыки решения задач на применение второго признака равенства треугольников. Перед решением задач необходимо повторить конспекты: «Треугольник. Равенство треугольников», «ЗАДАЧИ на Признаки равенства треугольников».

I уровень сложности (легкий)

Вариант 1 (уровень 1)

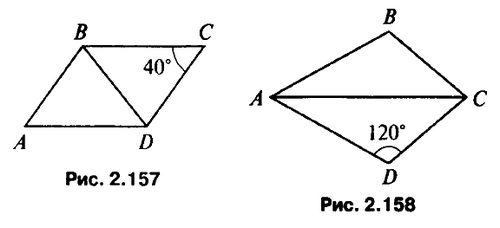
Дано: АВ = СD, ВС = DA, ∠C = 40° (рис. 2.157).
Доказать: ΔABD = ΔCDB. Найти: ∠A.
На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – медиана треугольника. Докажите, что MD = ND.
В треугольниках АВС и А₁В₁С₁ АВ = А₁В₁, ∠A = ∠A₁, ∠B = ∠B₁. Точки D и D₁ лежат соответственно на сторонах АС и А₁С₁, причем CD = C₁D₁. Докажите, что ΔBDC = ΔB₁D₁C₁. Сравните отрезки BD и B₁D₁.

Вариант 2 (уровень 1)

Дано: AD = АВ, CD = CB, D= 120° (рис. 2.158).
Доказать: ΔDAC = ΔBAC. Найти: ∠B.
На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – высота треугольника. Докажите, что MD = ND.
В треугольниках АВС и А₁В₁С₁ АВ = A₁B₁, АС = A₁C₁, ∠A = ∠A₁. Точки D и D₁ лежат соответственно на сторонах АС и A₁C₁, ∠DBC = ∠D₁B₁C₁. Докажите, что ΔBDC = ΔB₁D₁C₁. Сравните углы ВDC и B₁C₁D₁.

II уровень сложности (средний)

Вариант 1 (уровень 2)

Дано: АВ = СD, ВС = AD (рис. 2.159). Доказать: ∠A = ∠C.
На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки AM и CN. BD, медиана ΔAВС, пересекает отрезок MN в точке О. Докажите, что ВО – медиана ΔMBN.
В треугольниках АВС и А₁В₁С₁ АВ = A₁B₁, ∠А = ∠A₁, ∠B = ∠B₁. На сторонах ВС и В₁С₁ отмечены точки D и D₁ так, что ∠CAD = ∠C₁A₁D₁. Докажите, что: а) ΔADC = ΔA₁D₁C₁; б) ΔADB = ΔA₁D₁B₁.

Вариант 2 (уровень 2)

Дано: АВ = AD, ВС = DC (рис. 2.162). Доказать: ∠B = ∠D.
Дан равнобедренный ΔАВС с основанием АС и высотой BD. На лучах ВА и ВС вне треугольника АВС отложены равные отрезки AM и CN. Луч BD пересекает отрезок MN в точке О. Доказать, что ВО – высота ΔMBN.
В треугольниках DEC и D₁E₁C₁ DE = D₁E₁, ∠D = ∠D₁, ∠E = ∠E₁. На сторонах DE и D₁E₁ отмечены точки P и P₁ так, что ∠DCP = ∠D₁C₁P₁. Докажите, что: a) ΔDCP = ΔD₁C₁P₁; б) ΔCPE = ΔC₁P₁E₁.

III уровень сложности (сложный)

Вариант 1 (уровень 3)

Дано: АВ = CD, АС = BD (рис. 2.165). Доказать: ∠CAD = ∠BDA.
ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ME = PF. Докажите, что луч KN – биссектриса угла EKF (рис. 2.166).
В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно – так, что ВМ = BN. Докажите, что ΔBDM = ΔBDN.

Вариант 2 (уровень 3)

Дано: АВ = CD, АС = BD (рис. 2.168). Доказать: ∠ACB = ∠DBC.
ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ∠MKE = ∠PKF. Докажите, что ΔNЕК = ΔNFK (рис. 2.169).
В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне АВС отмечены точки М и N соответственно, так, что ∠BDM =∠BDN. Докажите, что ΔBDM = ΔBDN.

Самостоятельная работа № 6
Указания к решению и ОТВЕТЫ

С-6. I уровень сложности (ответы)

Геометрия 7 Атанасян Самостоятельная 6

С-6. II уровень сложности (ответы)

Задания и Ответы на Вариант 1 (уровень 2)

№ 1. Дано: АВ = СD, ВС = AD (рис. 2.159). Доказать: ∠A = ∠C.
Докажите самостоятельно.

№ 2. На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки AM и CN. BD, медиана ΔAВС, пересекает отрезок MN в точке О. Докажите, что ВО – медиана ΔMBN.

Доказательство:
1) ΔАВС – равнобедренный с основанием АС, и медиана BD является его биссектрисой (рис. 2.160).
2) ΔMBN – равнобедренный с основанием MN, так как МВ = BN (МВ = ВА– МА; BN = ВС – МС, ВА = ВС, МА = NC). BD – биссектриса ΔMBN, и по свойству биссектрисы равнобедренного треугольника она является медианой, т. е. ВО – медиана ΔMBN.

Доказательство:
а) ΔАВС = ΔА₁В₁С₁ по стороне и прилежащим к ней углам (АВ = A₁B₁, ∠A = ∠A₁, ∠B = ∠B₁ по условию задачи) (рис. 2.161). ΔADC = ΔA₁D₁C₁ по стороне и прилежащим к ней углам (АС = А₁С₁, ∠C = ∠C₁ из равенства треугольников АВС и А₁В₁С₁, ∠CAD = ∠C₁A₁D₁ по условию задачи).
б) Так как ΔADC = ΔA₁D₁C₁, то DC = D₁C₁, следовательно, равны отрезки BD и B₁D₁ (ВС = В₁С₁ из равенства треугольников АВС и А₁В₁С₁). Так как АВ = А₁В₁, ∠B = ∠B₁ из равенства треугольников АВС и А₁В₁С₁ и BD = В₁D₁, то ΔABD = ΔA₁B₁D₁ по двум сторонам и углу между ними.

Задания и Ответы на Вариант 2 (уровень 2)

№ 1. Дано: АВ = AD, ВС = DC (рис. 2.162). Доказать: ∠B = ∠D.
Докажите самостоятельно.

№ 2. Дан равнобедренный ΔАВС с основанием АС и высотой BD. На лучах ВА и ВС вне треугольника АВС отложены равные отрезки AM и CN. Луч BD пересекает отрезок MN в точке О. Доказать, что ВО – высота ΔMBN.

Доказательство:
1) ΔАВС – равнобедренный с основанием АС, и высота BD, проведенная из его вершины к основанию, является и его биссектрисой, т. е. ВО – биссектриса ∠ABC и ∠MBN тоже (рис. 2.163).
2) ΔMBN – равнобедренный с основанием MN (ВМ = ВА + AM, BN = ВС + CN; так как ВА = ВС и АМ = CN, то ВМ = BN). В равнобедренном ΔMBN биссектриса ВО, проведенная из его вершины к основанию, является и его высотой.

Доказательство:
а) ΔDEC = ΔD₁E₁C₁ по стороне и прилежащим к ней углам (DE = D₁E₁, ∠D = ∠D₁, ∠E = ∠E₁) (рис. 2.164).
Так как ΔDEC = ΔD₁E₁C₁, то DC = D₁C₁. Тогда ΔDCP= ΔD₁C₁P₁ по стороне и прилежащим к ней углам (DC = D₁C₁, ∠D = ∠D₁, ∠PCD= ∠P₁C₁D₁).
б) Так как ΔDEC = ΔD₁E₁C₁, тo EC = E₁C₁, ∠ECD = ∠E₁C₁D₁.
Так как ∠ECD = ∠E₁C₁D₁, ∠PCD = ∠P₁C₁D₁, a ∠ECP = ∠ECD – ∠DCP, ∠E₁C₁P₁ = ∠E₁C₁D₁ – ∠D₁C₁P₁, ∠ECP = ∠E₁C₁P₁.
Так как ЕС = E₁C₁ ∠E = ∠E₁, ∠ECP = ∠E₁C₁P₁, то ΔPEC = ΔP₁E₁C₁ по стороне и прилежащим к ней углам.

Геометрия 7 Атанасян Самостоятельная 6.

С-6. III уровень сложности (ответы)

Задания и Ответы на Вариант 1 (уровень 3)

№ 1. Дано: АВ = CD, АС = BD (рис. 2.165). Доказать: ∠CAD = ∠BDA.
Докажите самостоятельно.

№ 2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ME = PF. Докажите, что луч KN – биссектриса угла EKF (рис. 2.166).

Доказательство: ΔМЕК = ΔPFK по двум сторонам и углу между ними (ME = FP, МК = КР по условию задачи, ∠M = ∠P как углы при основании равнобедренного ΔMNP). Следовательно, КЕ= KF.
ΔKEN = ΔKFN по трем сторонам (КЕ = KF; KN – общая сторона; NE = NF, так как NE = MN – ME, NF = PN – PF, a MN = PN, ME = PF). Следовательно, ∠EKN = ∠FKN.
Так как ∠EKN = ∠FKN, то KN – биссектриса угла ∠EKF.

№ 3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно – так, что ВМ = BN. Докажите, что ΔBDM = ΔBDN.

Доказательство: Так как D – середина основания равнобедренного ΔАВС с основанием АС, то BD – медиана, а значит, и биссектриса ΔАВС. Следовательно, ∠ABD = ∠CBD (рис. 2.167).
∠NBA = ∠CBM как вертикальные.
∠NBD = ∠NBA + ∠ABD, a ∠MBD = ∠MBC + ∠CBD. Так как ∠ABD = ∠CBD, ∠MBC = ∠NBA, то ∠NBD = ∠MBD.
ΔNBD = ΔMBD по двум сторонам и углу между ними (NB = МВ; BD – общая сторона; ∠NBD = ∠MBD).

Задания и Ответы на Вариант 2 (уровень 3)

№ 1. Дано: АВ = CD, АС = BD (рис. 2.168). Доказать: ∠ACB = ∠DBC.
Докажите самостоятельно.

№ 2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ∠MKE = ∠PKF. Докажите, что ΔNЕК = ΔNFK (рис. 2.169).

Доказательство: ΔМЕК = ΔPFK по стороне и прилежащим к ней углам (МК = КР, так как К – середина МР; ∠MKE = ∠PKF по условию задачи; ∠M = ∠P как углы при основании равнобедренного ΔMNP).
Так как ΔМЕК = ΔPFK, то ME = PF, следовательно, EN = FN (EN = MN – ME, FN = PN – PF, a MN = FN как боковые стороны равнобедренного треугольника).
Так как ΔМЕК = ΔPFK, то КЕ = KF. ΔNEK = ΔNFK по трем сторонам (NK – общая сторона, NE = EF, ЕК = ЕК).

№ 3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне АВС отмечены точки М и N соответственно, так, что ∠BDM =∠BDN. Докажите, что ΔBDM = ΔBDN.

Доказательство: Так как D – середина основания АС равнобедренного ΔАВС, то BD – медиана и биссектриса ΔАВС. Следовательно, ∠ABD = ∠CBD (рис. 2.170).
∠NBA = ∠CBM как вертикальные. Поэтому ∠NBD = ∠MBD (∠NBD = ∠NBA + ∠ABD, ∠MBD = ∠MBC + ∠CBD, a ∠NBA = ∠CBM, ∠ABD = ∠CBD).
ΔBDM = ΔBDN по стороне и прилежащим к ней углам (BD – общая сторона, ∠NBD = ∠MBD, ∠BDM = ∠BDN).

Вы смотрели: Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 21. Решение задач на применение третьего признака равенства треугольников. Самостоятельная работа № 6 с ответами и решениями (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 6. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».