Собственные частоты и собственные вектора (6 видео)

Конечно-элементный анализ для всех. Часть 1

Джордж Лайрд, Ph.D., PE
Инженер-механик на PredictiveEngineer.com,
e-mail для связи: FEA@PredictiveEngineering.com.
Отправляйте свои комментарии к статье по адресу: DE-Editors@deskeng.com.

Мало кто проводит аналитическую работу просто из любопытства или от избытка свободного времени. Как правило, мы занимаемся ею тогда, когда не уверены в надежности конструкции в плане безопасности и окупаемости. В зависимости от типа риска наши опасения могут быть довольно слабыми, но, учитывая, как требовательны сегодня производители и насколько потребители склонны к судебным тяжбам, в случае неудачи вы можете оказаться в эпицентре серьезного разбирательства.

Если вы уже проводили анализ, вам должны быть знакомы понятия, используемые при анализе статического напряжения; задав нагрузку и граничные условия, вы сразу можете определить, удачна ли модель, по тому, что она окрашена в мягкие тона серого и голубого, без малейшего вкрапления красного. Однако подсознательно вас тревожит воздействие большого вибромотора или заводского оборудования, непрерывно работающего с частотой 12,5 Гц. Или вам необходимо прикрепить короб с электроникой к стене здания, расположенного в сейсмоактивной зоне, а ваш босс ставит под сомнение предложенный вами вариант конструкции монтажных кронштейнов. Как бы то ни было, мир статики вам подвластен. А как насчет всего остального?

В данном цикле статей мы вкратце рассмотрим основы динамического анализа и увидим, что они легко могут быть применены вами для проверки вашей конструкции на прочность и надежность при воздействии динамических нагрузок, будь то вибрация, землетрясение или даже запуск ракеты.

Содержание

Будем проще
На примере балки
На примере конструкции целлюлознобумажного производства
Поведение конструкции под воздействием динамической нагрузки
Итоговые расчеты
Основные этапы анализа собственных форм и частот колебаний
Собственные частоты и собственные вектора
Где учитесь?
Собственные частоты и собственные вектора
💡 Видео

Видео:Собственные векторы и собственные значения матрицыСкачать

Будем проще

Анализ статического напряжения — сущий пустяк для большинства специалистов, занимающихся аналитической работой. Эта процедура воспринимается как крайне понятная и простая: мы прикладываем фиксированную нагрузку и наблюдаем проистекающее статическое поведение (как правило, линейное при заданном линейном поведении материалов). В результате мы получаем несколько аккуратных прогибов и деформаций, которые благополучно соответствуют нашим ожиданиям относительно поведения конструкции. И хотя в ходе процесса могут возникнуть небольшие несоответствия, полученный конечный результат, как правило, представляется нашим техническим умам вполне логичным.

Динамическое поведение структуры также можно рассматривать в подобном ключе, достаточно только взглянуть на ситуацию под немного другим углом и подумать о том, как будет деформироваться наша структура в ходе динамического воздействия. Когда структура подвергается удару или некой меняющейся во времени нагрузке (переменной или стабильной), она реагирует на подобное воздействие весьма характерным образом. Если нагрузка не чрезмерна и структура под ее воздействием не разрушается и не подвергается пластической деформации, то динамическая реакция вашей структуры, скорее всего, будет линейной. То есть если нагрузку убрать и дать структуре вернуться в состояние покоя, то она вернется в исходное, недеформированное состояние. Тот же принцип следует использовать при анализе линейного статического напряжения: когда нагрузка исчезает, напряжение конструкции вновь обнуляется.

Что именно мы подразумеваем под характеристическим динамическим поведением? Все структуры имеют характеристический, или собственный, вид колебаний. Звук или нота колеблющейся гитарной струны — это типичный пример собственной частоты колебаний. При ударе по гитарной струне ее вибрация соответствует определенной ноте, или тону. Эта нота — и есть характеристическая частота струны.

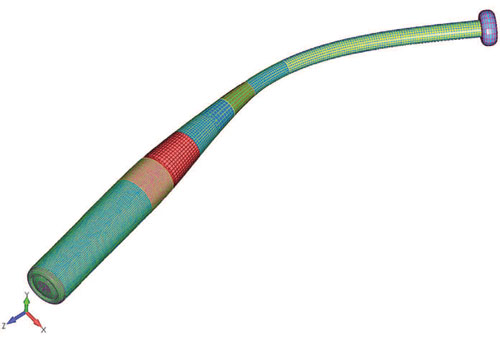
Другим примером могут послужить алюминиевые бейсбольные биты. Лучшие алюминиевые биты проектируются так, чтобы их характеристические колебания могли ограничить деформацию, которая происходит при ударе по мячу не оптимальной для удара частью биты. Каждая частота создает физическую деформацию или форму, и суммарная динамическая реакция биты является комбинацией всех форм ее собственных колебаний (рис. 1 и 2).

Рис. 1. Первая форма собственных колебаний алюминиевой бейсбольной биты фирмы NCAA

Рис. 2. Вторая форма собственных колебаний алюминиевой бейсбольной биты NCAA

В конечноэлементном анализе (КЭА) эти собственные частоты называются собственными частотами (eigenvalues), а их формы обозначаются как собственные векторы (eigenvectors) или собственные формы колебаний (eigenmodes). Эта терминология заимствована из немецкого языка, где eigen означает «характерный» или «свойственный для», и первоначально получила распространение среди математиков XIX века. В динамическом анализе вам также встретятся термины «нормальная форма колебаний» и «анализ нормальных колебаний». Слово «нормальное» применительно к слову «колебание» — это еще один синоним естественных, характерных, собственных (eigen) форм колебаний. Описывая формы колебаний, мы чаще всего будем использовать термин «нормальные колебания», чтобы подчеркнуть естественный, неизбежный характер реакции структуры.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

На примере балки

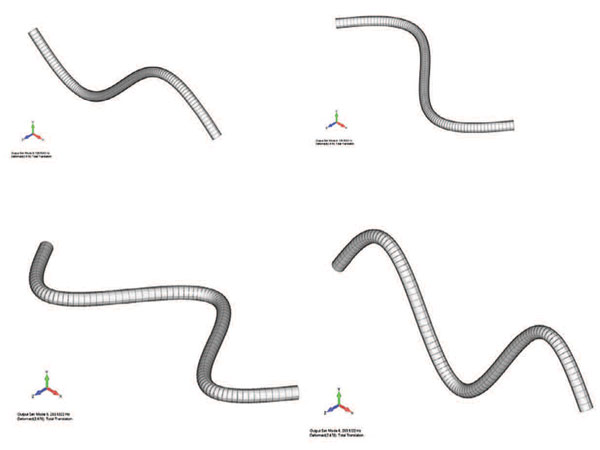
Если рассматривать свободно опертую балку (закрепленную с одного конца), ее собственные формы колебаний определяются геометрией, тогда как частота колебаний зависит от прочности и плотности. Просто? Взгляните на график первых трех форм колебаний нашей балки (рис. 3 и 4). Первые три формы балки обозначены четко, но отображаются попарно, чтобы охватить весь возможный диапазон движения данной балки. В трехмерном отображении первая форма может колебаться в 360градусном диапазоне по продольной оси. Численно процесс расчета собственных форм колебаний дает нам всего две ортогональные моды (формы), но эти две моды подразумевают вариации в диапазоне 360°.

Рис. 3. Балка в состоянии покоя плюс две первые формы ее собственных колебаний (два направления движения)

Рис. 4. Пары второй и третьей форм собственных колебаний свободно опертой балки

Все структуры имеют практически бесконечное количество собственных форм колебаний. К счастью, реакция структуры лежит в основном в низких частотах, так что высокими частотами мы можем в принципе пренебрегать. Эмпирическим путем доказано, что первые три формы колебаний отражают практически все возможные варианты реакции структуры, поэтому мы можем спокойно пренебречь высокими частотами (обоснование этого утверждения приведено в части II данного цикла статей).

Собственная частота колебаний, иначе говоря их собственные значения, зависит от жесткости и плотности балки. Таким образом, уравнение частоты колебаний для структур может быть представлено как

где К — жесткость структуры, а m — ее масса. Это на удивление простое уравнение дает нам всю основную информацию о структуре. Классический способ графического представления данного уравнения — это тело, подвешенное на пружине, причем тело может двигаться только вверх и вниз либо с одной степенью свободы (DOF), согласно терминологии конечноэлементного анализа.

Собственный вектор колебаний данной системы — колебания вверх и вниз.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

На примере конструкции целлюлознобумажного производства

В производственных структурах применяется то же самое уравнение. Собственная частота колебаний структуры определяется той же формулой:

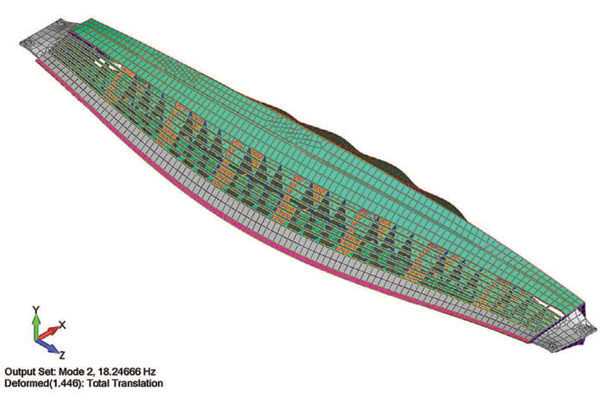
Например, рассмотрим конструкцию, используемую в целлюлознобумажном производстве. Данная структура имеет 10 м в длину и изготовлена из нержавеющей стали. На целлюлознобумажном комбинате рабочая частота составляет порядка 9 Гц. Если нормальная частота колебаний конструкции практически равна рабочей частоте, структура резонирует и разрушается. А главное, при этом серьезно пострадает предприятие, в которое вложен не один миллион долларов (рис. 5 и 6).

Рис. 5. Первая форма колебаний оборудования целлюлозно-бумажного комбината

Рис. 6. Вторая собственная форма колебаний оборудования целлюлозно-бумажного комбината

Параметры исходной конструкции давали первую форму колебаний при частоте 8,4 Гц, а это равносильно катастрофе. Рассматриваемая доска изготавливается из стальных пластин толщиной 9,5 мм, поэтому нашей первой мыслью в направлении оптимизации конструкции было простое увеличение толщины пластин. Мы прорабатывали данный вариант в течение нескольких дней, но при увеличении толщины пластин масса структуры также возрастала, повышаясь одновременно с жесткостью (см. приведенное выше уравнение). В результате всех этих усилий мы получили лишь незначительное улучшение (резонансная частота колебаний

11 Гц) при толщине пластин 25 мм, но такое изменение конструкции стоило бы предприятию огромных денег.

На этом мы отказались от спешных попыток найти решение проблемы и задумались над тем, как формируется прочность в вытянутых тонких структурах. Мы поняли, что связь между нижней и верхней поверхностями доски очень слабая. Эта догадка привела нас к идее добавления диагональных стальных стержней, соединяющих верхнюю и нижнюю поверхности и позволивших бы нам сохранить толщину пластин 9,5 мм. Обновленная конструкция была протестирована на компьютере и показала первую собственную частоту колебаний 13 Гц. Теперь собственная частота колебаний изделия стала гораздо больше, чем рабочая частота комбината, резонанс стал невозможен, а система приобрела динамическую устойчивость. Кроме того, сохранение толщины пластин (9,5 вместо 25 мм) означало вдвое меньшую стоимость внесения изменений по сравнению с первым малоэффективным вариантом доработки конструкции.

Видео:Собственные значения и собственные векторы. ТемаСкачать

Поведение конструкции под воздействием динамической нагрузки

Если на структуру действует кратковременная или изменяющаяся во времени нагрузка (например, электромотор создает постоянную, синусоидально меняющуюся нагрузку) и если собственное значение колебаний конструкции ниже или выше, чем частота возбуждения, то поведение структуры будет таким же, как при воздействии статической нагрузки. Допустим, у нас есть структура с собственным значением колебаний в 10 Гц и она подвергается кратковременному удару (например, полусинусоидальной волной с частотой 10 Гц). В этом случае можно ожидать, что структура будет вибрировать от удара, а затем постепенно вернется в исходное состояние покоя в отсутствие воздействия.

Однако если структура подвергнется динамической нагрузке, изменяющейся во времени (например, воздействие синусоидальной волны частотой 10 Гц), то произойдет резонанс. Если поглощения вибрации практически нет (как у металлов или пластика), можно будет наблюдать классический гармонический резонанс, подобный тому, что привел к обрушению Тэкомского моста в 1940 году.

Именно резонанс разрушает конструкции, а наихудшая разновидность резонанса возникает тогда, когда на изделие снова и снова оказывается переменное возбуждающее воздействие. Наиболее эффективным способом предотвращения подобной неприятности является создание такой конструкции, собственная частота колебаний которой выше или ниже, чем ее рабочая частота; решение этой задачи лежит в основе проведения анализа собственных частот колебаний.

Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Итоговые расчеты

В предыдущих выкладках мы ни разу не упомянули амплитуду колебаний. То есть мы говорили об их частоте и форме, но вопрос амплитуды остался незатронутым. В частотном анализе (анализе собственной частоты колебаний) рассматривается структура без приложения к ней какойлибо нагрузки. Без нагрузки (то есть без воздействия какихлибо сил или давления) прогнозировать реальный вид вынужденных колебаний невозможно. Выведение собственных форм колебаний (формы допустимых видов деформации) предполагает проведение математических расчетов, ход которых можно посмотреть в любом учебнике. Однако ключевым для нас является решение уравнения динамики:

Если пренебрегать демпфированием (С) (а это можно смело делать в отношении многих конструкций), а прикладываемая сила f(t) равна нулю, уравнение принимает более краткую и удобную форму:

Это ключевое уравнение для анализа свободных колебаний, показывающее, что только масса и прочность структуры влияют на формы ее колебаний.

Для решения данного уравнения воспользуйтесь вашим любимым пособием по математике. Суть вопроса в том, что вычисление собственной частоты колебаний структуры сводится к компактной формуле:

И поскольку при расчете собственной частоты колебаний конструкции никакие силы не учитываются, связанные с ним собственные формы колебаний не поддаются измерению. В этом случае ваша программа для конечноэлементного анализа регулирует формы собственных колебаний таким образом, чтобы максимальное перемещение внутри каждой формы приближалось к 1.0 или к некой величине в зависимости от массы структуры. Когда данные формы свободных колебаний отображаются в программе для конечноэлементного анализа, мы видим воображаемую амплитуду; такая визуализация может стать проблемой для многих новичков, впервые отважившихся погрузиться в мир динамического анализа. Но более подробно о ее особенностях рассказано в части 2 данной статьи.

Видео:Собственные значения и собственные векторыСкачать

Основные этапы анализа собственных форм и частот колебаний

Определите, какой тип нагрузки может воздействовать на вашу конструкцию и может ли эта нагрузка вызвать резонанс. Постарайтесь определить частотные характеристики вашей нагрузки и убедитесь, что они не совпадают с собственными частотами вашей конструкции.

Проведите частотный анализ и посмотрите на первые три собственные частоты колебаний. Проверьте, попадают ли они в определенную вами опасную зону.

Если собственные частоты не попадают в диапазон частот вашей нагрузки, можете прекращать работу. Вы закончили ее, и всё получилось правильно.

Если собственные частоты вашего изделия попадают в диапазон опасных частот и вы не можете изменить конструкцию для улучшения ситуации, тогда продолжайте читать наши статьи. В них мы расскажем, почему ваше положение не так уж и плохо.

Видео:Линал 1.8 Собственные векторы и собственные числаСкачать

Собственные частоты и собственные вектора

Найдем такие вектора (называются собственными векторами) v
и такие числа — значения (называются собственными значениями) l
матрицы A, для v, l и A выполняется:
A*v = l*v.

Также вычисляется кратность собственных значений и находит характеристическое уравнение матрицы.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Где учитесь?

Для правильного составления решения, укажите:

Видео:Собственные векторы и собственные значенияСкачать

Собственные частоты и собственные вектора

Глава 3. Работа с векторами и матрицами

3.8 Собственные числа и собственные векторы матриц

Собственные числа и собственные векторы матриц

В технических расчетах весьма актуальна задача определения собственных чисел и собственных векторов квадратных матриц. В MathCAD имеется несколько встроенных функций для решения стандартных и нестандартных задач.

Рассмотрим стандартную задачу на собственные числа A · L =λ· L или ( A –λ·Е)· L =0, где Е – единичная матрица, А – квадратная матрица, λ – вектор собственных чисел, L – спектр собственных векторов (рис. 3.15 ).

Для решения стандартной задачи используются следующие функции:

– eigenvals ( A ) –вычисляет вектор собственных чисел матрицы А, превращающий ее в диагональную матрицу;

– eigenvecs ( A ) – вычисляет спектр собственных векторов матрицы А. Результат расчета – матрица, каждый столбец которой А i > представляет собой нормированный собственный вектор для одного из собственных чисел λ _{i .}

Пример стандартной задачи: по заданному тензору напряжений найти три главных напряжений (собственные числа) и соответствующие им направляющие косинусы для нормалей к трем главным площадкам (собственные векторы).

Стандартная задача на собственные числа

или , где Е — единичная матрица

собственные числа собственные векторы

Создание диагональной матрицы из собственных чисел

Рис. 3. 15 Определение собственных чисел квадратной матрицы

Нестандартная задача на собственные числа имеет вид A · L =λ·В· L или ( A –λ·В)· L =0, где А и В – квадратные матрицы (неединичные), λ – вектор собственных чисел; L – спектр собственных векторов (рис. 3.1 6 ).

Нестандартная задача на собственные числа

или , где А и В симметричные матрицы

собственные числа собственные векторы

Рис. 3. 16 Обобщенные собственные числа матрицы

Пример нестандартной задачи: определение собственных частот колебаний упругих систем. В этой задаче собственное число λ=ω 2 – квадрат собственной частоты колебаний, собственный вектор L i > – форма для собственной частоты ω _i .

Для решения нестандартной задачи используются следующие функции:

– genvals ( A , B ) – вычисляет вектор обобщенных собственных чисел λ _i ;

– genvecs ( A , B ) – вычисляет спектр собственных векторов. Результат расчета – матрица, каждый столбец которого L i > соответствует собственному числу λ _i .

Вектор собственных чисел можно преобразовать в диагональную матрицу с помощью функции diag (). Результат ее действия – диагональная матрица, на главной диагонали которой расположены элементы вектора λ.