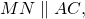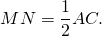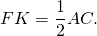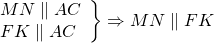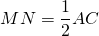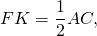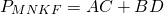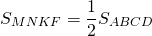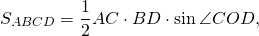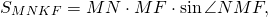В этой статье мы рассмотрим все основные свойства и признаки четырехугольников.
Для начала я расположу все виды четырехугольников в виде такой сводной схемы:
Схема замечательна тем, что четырехугольники, стоящие в каждой строке обладают ВСЕМИ СВОЙСТВАМИ ЧЕТЫРЕХУГОЛЬНИКОВ, РАСПОЛОЖЕННЫХ НАД НИМИ. Поэтому запоминать надо совсем немного.
Трапеция — это четырехугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами.
1. В трапеции сумма углов, прилежащих к боковой стороне равна 180°: А+В=180°, C+D=180°
2. Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне: 
3. Биссектрисы смежных углов трапеции пересекаются под прямым углом.
4.Трапеция называется равнобедренной, если ее боковые стороны равны:
В равнобедренной трапеции
- углы при основании равны,
- проекции боковых сторон на основание равны:
.
.5. Площадь трапеции равна произведению полусуммы оснований на высоту:
Параллелограм — это четырехугольник, у которого противоположные стороны попарно параллельны: 
В параллелограмме:
- противоположные стороны и противоположные углы равны
- диагонали параллелограмма делятся точкой пересечения пополам:
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.
Площадь параллелограмма равна произведению основания на высоту:
или произведению сторон на синус угла между ними:
:
Ромб — это параллелограмм, у которого все стороны равны:
- противоположные углы равны
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали ромба являются биссектрисами углов
Площадь ромба равна половине произведения диагоналей:
или произведению квадрата стороны на синус угла между сторонами:
Прямоугольник — это параллелограмм, у которого все углы прямые:
- Диагонали прямоугольника равны.
- Диагонали точкой пересечения делятся пополам.
Площадь прямоугольника равна произведению его сторон:
.
Квадрат — это прямоугольник, у которого все стороны равны
Квадрат — это ромб, у которого все углы прямые.
Соответственно: квадрат обладает свойствами ромба и прямоугольника:
- все углы равны 90 градусов
- диагонали точкой пересечения делятся пополам
- диагонали взаимно перпендикулярны
- диагонали являются биссектрисами углов
- диагонали равны
Площадь квадрата равна квадрату его стороны.
Площадь квадрата равна половине произведения диагоналей.
И.В. Фельдман, репетитор по математике.
Видео:Формула для биссектрисы треугольникаСкачать
Биссектриса параллелограмма — свойства, признаки и теоремы
Аксиома параллельности прямых, которая приведена Евклидом в книге «Начала», служит основой для доказательства многих свойств биссектрисы параллелограмма. О них знали пифагорейцы. Но понятие о самой фигуре ввел именно Евклид. Она представляет собой четырехугольник с параллельными противоположными сторонами.
Видео:№133. Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольникСкачать
Равнобедренный треугольник в параллелограмме
Биссектриса параллелограмма может быть проведена из вершины острого или тупого угла фигуры. Доказательство теоремы о равнобедренности образуемых прямой треугольников в этих случаях имеет аналогичный порядок. Чтобы доказать утверждение, нужно знать признак равнобедренности треугольника:
С помощью аналогичных рассуждений можно доказать, что биссектриса тупого угла параллелограмма делит противоположную сторону на отрезки и отсекает от него равнобедренный треугольник.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать
Точка пересечения прямых
Согласно свойству, проведенные из смежных углов параллелограмма биссектрисы пересекаются в точке на противоположной стороне, если она в 2 раза больше меньшей. Доказать это утверждение можно следующим способом:
Доказательство свойства позволяет предположить, что биссектрисы смежных углов пересекаются внутри либо вне параллелограмма. При этом одна сторона больше или меньше половины другой. Если ее величина больше половины соседней, значит прямые пересекутся внутри фигуры.
Биссектрисы, проведенные через смежные углы, пересекаются с продолжением противоположных сторон параллелограмма в вершинах ромба. В зависимости от величины другой стороны, ромб совпадает с ним либо обладает большим или меньшим периметром. Если частить с построением этой фигуры, то длины сторон параллелограмма будут бесконечными.
Видео:Свойство биссектрисы треугольника с доказательствомСкачать
Свойства односторонних углов
Параллелограмм АВСД имеет смежные углы при параллельных прямых АВ и СД, обозначенные а1 и а2. Для доказательства теоремы о перпендикулярности биссектрис нужно знать свойства смежных углов, сумма которых равна 180 градусам.
Поскольку биссектрисы можно провести внутри острого или тупого угла параллелограмма, то величину смежного с ним внешнего угла можно сложить, получив 180 градусов. Если обозначить их через АО и ДЕ, то углы ОАВ и ЕДС будут равны половинам а1 и а2 соответственно. Так как а1 + а2 = 180, то (а1 + а2) / 2 = 90, значит АО и ДЕ образуют прямой угол АКД.
Применять свойство биссектрис можно при нахождении периметра фигуры. Должны быть известны данные о соотношениях или длинах отрезков, образованных при пересечении противолежащей стороны биссектрисой. Например, она делит на отрезки ВК и КС сторону параллелограмма ABCD, величины которых известны.
Формула определения периметра будет иметь вид: P=2 (n+n+m). Где ВС=BК+КC=n+m, а АВ=ВК=n по свойству биссектрисы. С учетом признака равнобедренности треугольника можно построить эту прямую, дополнив рисунок фигуры без транспортира с помощью циркуля.
Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать
Противолежащие углы и биссектрисы
Согласно свойству параллельных прямых, биссектрисы a и b проходят параллельно друг другу. Они образуют внутри фигуры со сторонами mnkp другой параллелограмм, следовательно, он обладает параллельными противоположными сторонами. Прямые, на которых они лежат, соответствуют сторонам исходной фигуры, поэтому ее биссектрисы a и b являются равными.
Углы, которые образованы отрезками a и m, а также b и k, согласно свойствам биссектрис и параллелограммов, равны. Противолежащие равные по величине углы, образованные отрезками mp и nk, можно разделить пополам. Прямая b, пересекающая отрезки n и p, образует с ними накрест лежащие углы, признак которых состоит в их равенстве. Они равны разделенным пополам противоположным и являются соответственными при параллельных прямых n и p.
Видео:Cекретное свойство биссектрисыСкачать
Вершины образуемого прямоугольника
Биссектрисы параллелограмма пересекаются в точках, представляющих собой вершины прямоугольника, что можно доказать следующим образом:
Аналогичным способом можно доказать параллельность других сторон прямой СД. Следовательно, диагональ КР образованного биссектрисами параллелограмма прямоугольника КМРО содержит точки Х и Т. Доказательство предполагает следующее равенство: КР = КХ + ХТ + ТР = ХС + СД + ТД = ВС + СД, поэтому величина диагонали равна сумме двух смежных сторон параллелограмма.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать
Ромб и его диагонали
Параллелограмм, имеющий биссектрису, которая совпадает с его диагональю, представляет собой ромб. Чтобы доказать это, нужно провести диагональ AC, соединяющую противоположные вершины ABCD. Способ доказательства теоремы основан на равенстве противолежащих углов параллелограмма.
Согласно свойству биссектрисы, отрезок АС делит пополам углы BCD и BAD. Они имеют одинаковую величину, поскольку противоположные углы равны. Диагональ АС — основание треугольников ACB и ACD. Согласно признаку равнобедренности АВ и АС, а также AD и CD, равны между собой. По свойству равенства противоположных сторон параллелограмма AB = CD и AD = BC.
Фигура ABCD, представляющая собой по условию параллелограмм, имеет равные по величине AB, AD, BC и CD в соответствии с доказательством. Отсюда следует, что параллелограмм ABCD по определению ромб. В нем биссектриса АС — это его диагональ.
Видео:Геометрия Доказать, что если в четырехугольнике диагонали лежат на биссектрисах его углов, то такойСкачать
Примеры решения задач
Биссектрисы смежных углов параллелограмма пересеклись в точке на его противолежащей стороне. Зная его меньшую сторону, можно найти большую, а также наоборот. Допустим, что длина меньшей стороны фигуры составляет 5 сантиметров.
Обозначив вершины фигуры A, B, C, D, а точку на AD буквой Р, достаточно иметь в виду, что AD=AР+РD=AB+CD. Это доказывает признак равенства накрест лежащих углов СВР и АРВ, а также ВСР и СРD при параллельных прямых. Формула для нахождения большей стороны будет иметь вид: AD=2AB=10, поскольку AB = CD. При необходимости найти меньшую можно по формуле: AD=AB/2.
По условию задачи биссектриса, исходящая из острого угла параллелограмма, разделяет его противоположную сторону на отрезки 73 мм и 54 мм, если считать от вершины тупого угла. Требуется вычислить периметр параллелограмма ABCD. Точка Е делит сторону ВС на отрезки заданной длины, поскольку АЕ — биссектриса угла ВАD. Эта прямая представляет собой секущую для параллельных AD и BC.
Отсекая равнобедренный треугольник АВЕ, биссектриса ВЕ является его основанием, поэтому сторона параллелограмма АВ равна отрезку ВЕ, длина которого по условию 73 мм. В сумме ВЕ и ЕС равны ВС, что составляет 127 мм. Отсюда периметр ABCD соответствует удвоенной сумме его сторон: Р = 2 (73+127) = 400 мм. Чтобы найти большую сторону параллелограмма ABCD при известном периметре 128 мм, можно использовать аналогичное доказательство равнобедренности треугольника.
По условию соотношение отрезков, образуемых точкой пересечения биссектрисы DЕ с противоположной стороной ВС, равно 4:3, если считать от острого угла при вершине А. Из равенства противоположных сторон ABCD и признака равнобедренного треугольника следует AD=BC=АЕ=4х, а ЕВ=3х, поэтому CD=АЕ+ЕВ=4х+3х=7х. Зная периметр ABCD, можно составить уравнение Р=2 (7х+4х)=128. Отсюда 22х=128, а х=32, поэтому большая сторона параллелограмма CD=32*7=224 мм.
Видео:БИССЕКТРИСА В ТРАПЕЦИИ. Мат в 3 хода!Скачать
Теорема Вариньона
В школьном курсе теорема Вариньона часто фигурирует в качестве обычной задачи, в которой требуется доказать, что середины сторон четырёхугольника являются вершинами параллелограмма.
Её доказательство основано на свойствах средней линии треугольника.
Середины сторон четырёхугольника являются вершинами параллелограмма.
Дано: ABCD — четырёхугольник,
M, N, K, F — середины его сторон.
Доказать : MNKF — параллелограмм.
1) Проведём диагональ AC.
2) Рассмотрим треугольник ABC.
Так как точки M и N — середины сторон AB и BC, отрезок MN — средняя линия треугольника ABC.
3) Аналогично, FK — средняя линия треугольника ADC и
4) По признаку параллельности прямых, две прямые, параллельные третьей прямой, параллельны между собой:
5) В четырёхугольнике MKNF противоположные стороны параллельны и равны. Следовательно, MKNF — параллелограмм (по признаку).
Что и требовалось доказать.
Поскольку в школьном курсе геометрии рассматриваются только выпуклые четырёхугольники, доказательство приведено только для этого случая. Но и для невыпуклых четырёхугольников (в том числе, и для самопересекающихся), теорема также верна (доказывается аналогично).
Параллелограмм, образованный серединами сторон четырёхугольника, называется параллелограммом Вариньона (вариньоновским, вариньоновым).
Периметр параллелограмма Вариньона равен сумме диагоналей исходного параллелограмма:
(так как стороны MNKF равны половине диагонали AC или BD).
Площадь параллелограмма Вариньона равна половине площади исходного параллелограмма:
углы COD и NMF равны (как внутренние накрест лежащие при параллельных прямых AC и MN и секущей BD),
📹 Видео
Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать
3 свойства биссектрисы #shortsСкачать
№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать
Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать
#26. EGMO-2022, Problem 6Скачать
Биссектрисы трапеции | Осторожно, спойлер! | Борис Трушин !Скачать
Найдите биссектрису треугольникаСкачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать
Геометрия Биссектрисы углов A и C параллелограмма ABCD пересекают диагональ BD в точках E и FСкачать
Найти угол между биссектрисой и высотойСкачать
