Abcd четырехугольник вписанный в окружность m точка пересечения его диагоналей

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Ваш ответ

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,061
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Диагонали четырёхугольника ABCD, вписанного в окружность, взаимно перпендикулярны. Из вершин В и ССкачать

Олимпиадные задания по математике 8 — 11 класс

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Олимпиадные задания по математике 8 — 11 класс

Видео:Доказать, что точки лежат на одной окружностиСкачать

Олимпиадные задания по математике 8 класс

1. На доске была нарисована система координат и отмечены точки A(1;2) и B(3;1). Систему координат стерли. Восстановите ее по двум отмеченным точкам.

2. В некотором треугольнике биссектрисы двух внутренних углов продолжили до пересечения с описанной окружностью и получили две равные хорды. Верно ли, что треугольник равнобедренный?

3. В правильном шестиугольнике АВСDEF на прямой AF взята точка X так, что угол XСD = 45 o . Найдите угол FXE.

4. Около четырехугольника ABCD можно описать окружность. Точка p – основание перпендикуляра, опущенного из точки А на прямую ВС, Q – из А на DC, R – из D на АВ и Т – из D на ВС. Докажите, что точки p, Q, R и T лежат на одной окружности.

5. Восстановите остроугольный треугольник по ортоцентру и серединам двух сторон.

6. Противоположные стороны выпуклого шестиугольника ABCDEF параллельны. Назовем его «высотами» векторы с концами на прямых, содержащих противолежащие стороны, перпендикулярные им и направленные от AB к DE, от EF к BC и от CD к AF. Докажите, что вокруг этого шестиугольника можно описать окружность тогда и только тогда, когда сумма его «высот» равна нулевому вектору.

Видео:Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

Олимпиадные задания по математике 8 класс

1. Биссектриса угла В и биссектриса внешнего угла D прямоугольника ABCD пересекают сторону AD и прямую АВ в точках М и К соответственно. Докажите, что отрезок МК равен и перпендикулярен диагонали прямоугольника.

2. В равнобедренном треугольнике АВС на боковой стороне ВС отмечена точка М так, что отрезок СМ равен высоте треугольника, проведенной к этой стороне, а на боковой стороне АВ отмечена точка К так, что угол КМС – прямой. Найдите угол АСК .

3. Из листа бумаги в клетку вырезали квадрат 2×2. Используя только линейку без делений и не выходя за пределы квадрата, разделите диагональ квадрата на 6 равных частей.

4. В трапеции ABCD : AB = BC = CD , CH – высота. Докажите, что перпендикуляр, опущенный из Н на АС , проходит через середину BD .

5. Пусть AA ₁ и BB ₁ – высоты неравнобедренного остроугольного треугольника АВС , М – середина АВ . Окружности, описанные около треугольников AMA ₁ и BMB ₁ пересекают прямые АС и ВС в точках К и L соответственно. Докажите, что К , М и L лежат на одной прямой.

6. Один треугольник лежит внутри другого. Докажите, что хотя бы одна из двух наименьших сторон (из шести) является стороной внутреннего треугольника.

Видео:#29. Регион ВсОШ 2023, 9.5Скачать

Олимпиадные задания по математике 9 класс

1. Постройте треугольник по стороне, противолежащему углу и медиане, проведенной к другой стороне ( исследование вопроса о количестве решений не требуется ).

2. В выпуклом четырехугольнике ABCD Ð ABC = 90 0 , Ð BAC = Ð CAD , AC = AD , DH — высота треугольника ACD . В каком отношении прямая BH делит отрезок CD ?

3. Внутри отрезка АС выбрана произвольная точка В и построены окружности с диаметрами АВ и ВС . На окружностях (в одной полуплоскости относительно АС ) выбраны соответственно точки M и L так, что Ð MBA = Ð LBC . Точки K и F отмечены соответственно на лучах ВМ и BL так, что BK = BC и BF = AB . Докажите, что точки M , K , F и L лежат на одной окружности.

4. В треугольнике ABC M — точка пересечения медиан, O — центр вписанной окружности, A’ , B’ , C’ — точки ее касания со сторонами BC , CA , AB соответственно. Докажите, что, если CA’ = AB , то прямые OM и AB перпендикулярны.

5. Дан треугольник АВС . Точка О 1 — центр прямоугольника ВСDE , построенного так, что сторона DE прямоугольника содержит вершину А треугольника. Точки О 2 и О 3 являются центрами прямоугольников, построенных аналогичным образом на сторонах АС и АВ соответственно. Докажите, что прямые АО 1 , ВО 2 и СО 3 пересекаются в одной точке.

6. На плоскости расположен круг. Какое наименьшее количество прямых надо провести, чтобы, симметрично отражая данный круг относительно этих прямых (в любом порядке конечное количество раз), можно было накрыть им любую заданную точку плоскости?

Видео:#26. EGMO-2022, Problem 6Скачать

Олимпиадные задания по математике 9 класс

9.1. В выпуклом четырехугольнике АВС D Е – середина CD , F – середина А D , K – точка пересечения АС и ВЕ . Докажите, что площадь треугольника BKF в два раза меньше площади треугольника АВС .

9.2. Постройте треугольник АВС по углу А и медианам, проведенным из вершин В и С .

9.3. Дан квадрат ABCD . Найдите геометрическое место точек M таких, что Ð AMB = Ð CMD .

9.4. Треугольник ABC вписан в окружность. Через точки A и B проведены касательные к этой окружности, которые пересекаются в точке p . Точки X и Y – ортогональные проекции точки p на прямые AC и BC . Докажите, что прямая XY перпендикулярна медиане треугольника ABC , проведенной из вершины C .

9.5. Диагонали вписанного четырёхугольника ABCD пересекаются в точке M , Ð AMB = 60 ° . На сторонах AD и BC во внешнюю сторону построены равносторонние треугольники ADK и BCL . Прямая KL пересекает описанную около ABCD окружность в точках p и Q . Докажите, что pK = LQ .

9.6. Длина каждой стороны и каждой не главной диагонали выпуклого шестиугольника не превосходит 1. Докажите, что в этом шестиугольнике найдется главная диагональ, длина которой не превосходит 2 деленное на корень из 3 .

Видео:Четырехугольник АВСD со сторонами АВ=12 иСD=13 вписан в окружность. 27 вариант Ященко ОГЭ задача 25Скачать

Олимпиадные задания по математике 9 класс

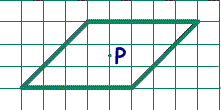
1. На рисунке изображен параллелограмм и отмечена точка p пересечения его диагоналей. Проведите через p прямую так, чтобы она разбила параллелограмм на две части, из которых можно сложить ромб.

2. Квадрат и прямоугольник одинакового периметра имеют общий угол. Докажите, что точка пересечения диагоналей прямоугольника лежит на диагонали квадрата.

4. Постройте треугольник по стороне, радиусу вписанной окружности и радиусу вневписанной окружности, касающейся этой стороны. (Исследование проводить не требуется.)

5. В некоторой точке круглого острова радиусом 1 км зарыт клад. На берегу острова стоит математик с прибором, который указывает направление на клад, когда расстояние до клада не превосходит 500 м. Кроме того, у математика есть карта острова, на которой он может фиксировать все свои перемещения, выполнять измерения и геометрические построения. Математик утверждает, что у него есть алгоритм, как добраться до клада, пройдя меньше 4 км. Может ли это быть правдой?

6. Фиксированы две окружности w₁ и w₂, одна их внешняя касательная l и одна их внутренняя касательная m. На прямой m выбирается точка X, а на прямой l строятся точки Y и Z так, что XY и XZ касаются w₁ и w2 соответственно, а треугольник XYZ содержит окружности w₁ и w₂. Докажите, что центры окружностей, вписанных в треугольники XYZ , лежат на одной прямой.

Видео:Геометрия Четырехугольник оказался вписанным Задача №26 ОГЭСкачать

Олимпиадные задания по математике 10 класс

10.1. Е и F – середины сторон ВС и AD выпуклого четырехугольника АВС D . Докажите, что отрезок EF делит диагонали АС и BD в одном и том же отношении.

10.2. Существует ли в пространстве замкнутая самопересекающаяся ломаная, которая пересекает каждое свое звено ровно один раз, причем в его середине?

10.3. На доске была нарисована окружность с отмеченным центром, вписанный в нее четырехугольник, и окружность, вписанная в него, также с отмеченным центром. Затем стерли четырехугольник (сохранив одну вершину) и вписанную окружность (сохранив ее центр). Восстановите какую-нибудь из стертых вершин четырехугольника, пользуясь только линейкой и проведя не более шести линий.

10.4. В треугольнике АВС : М – точка пересечения медиан, О – центр вписанной окружности. Докажите, что если прямая ОМ параллельна стороне ВС , то точка О равноудалена от сторон АВ и АС .

10.5. Трапеция АВС D с основаниями AB и CD вписана в окружность. Докажите, что четырехугольник, образованный ортогональными проекциями любой точки этой окружности на прямые AC , BC , AD и BD , является вписанным.

10.6. В тетраэдре DABC : Ð ACB = Ð ADB , ( С D ) ^ ( АВС ). В треугольнике АВС дана высота h , проведенная к стороне АВ , и расстояние d от центра описанной окружности до этой стороны. Найдите длину CD .

Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Олимпиадные задания по математике 10 класс

1. Каждый из двух подобных треугольников разрезали на два треугольника так, что одна из получившихся частей одного треугольника подобна одной из частей другого треугольника. Верно ли, что оставшиеся части также подобны?

2. Даны радиусы r и R двух непересекающихся окружностей. Общие внутренние касательные этих окружностей перпендикулярны. Найдите площадь треугольника, ограниченного этими касательными, а также общей внешней касательной.

3. Дан четырехугольник ABCD. A’, B’, C’ и D’ – середины сторон BC, CD, DA и AB соответственно. Известно, что AA’ = CC’ и BB’ = DD’. Верно ли, что ABCD параллелограмм?

4. В треугольнике АВС угол А равен 120 o . Докажите, что расстояние от центра описанной окружности до ортоцентра равно АВ + АС.

6. Есть два платка: один в форме квадрата, другой – в форме правильного треугольника, причем их периметры одинаковы. Существует ли многогранник, который можно полностью оклеить этими двумя платками без наложений (платки можно сгибать, но нельзя резать)?

6. Дан треугольник ABC и точки p и Q. Известно, что треугольники, образованные проекциями p и Q на стороны ABC, подобны (соответствуют друг другу вершины, лежащие на одних и тех же сторонах исходного треугольника). Докажите, что прямая pQ проходит через центр описанной окружности треугольника ABC.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Олимпиадные задания по математике 11 класс

1. AD и BE – высоты треугольника АВС . Оказалось, что точка C’ , симметричная вершине С относительно середины отрезка DE , лежит на стороне AB . Докажите, что АВ – касательная к окружности, описанной около треугольника DEC’ .

2. Прямая а пересекает плоскость α . Известно, что в этой плоскости найдутся 2011 прямых, равноудаленных от а и не пересекающих a. Верно ли, что а перпендикулярна α ?

3. Дана неравнобокая трапеция ABCD ( AB || CD ). Произвольная окружность, проходящая через точки А и В , пересекает боковые стороны трапеции в точках p и Q , а диагонали – в точках M и N . Докажите, что прямые pQ , MN и CD пересекаются в одной точке.

4. Докажите, что любой жесткий плоский треугольник T площади меньше четырёх можно просунуть сквозь треугольную дырку Q площади 3.

5. В выпуклом четырехугольнике ABCD : AC ⊥ BD , ∠ BCA = 10°, ∠ BDA = 20°, ∠ BAC = 40°. Найдите ∠ BDC . ( Ответ выразите в градусах. )

6. Пусть AA ₁, BB ₁ и CC ₁ – высоты неравнобедренного остроугольного треугольника АВС ; окружности, описанные около треугольников АВС и A ₁ B ₁ C , вторично пересекаются в точке Р , Z – точка пересечения касательных к описанной окружности треугольника АВС , проведённых в точках А и В . Докажите, что прямые АР , ВС и ZC ₁ пересекаются в одной точке.

Видео:ЕГЭ 2017 Четырехугольник и окружность (Планиметрия) Задание 16Скачать

Олимпиадные задания по математике 11 класс

1. Существуют ли два таких четырехугольника, что стороны первого меньше соответствующих сторон второго, а соответствующие диагонали больше?

2. Трапеция ABCD и параллелограмм MBDK расположены так, что стороны параллелограмма параллельны диагоналям трапеции (см. рис.). Докажите, что площадь зеленой части равна сумме площадей синих частей.

3. В остроугольном треугольнике АВС проведены высоты АА₁ и ВВ₁. Докажите, что перпендикуляр, опущенный из точки касания вписанной окружности со стороной ВС на прямую АС, проходит через центр вписанной окружности треугольника А₁СВ₁.

4. На медианах треугольника как на диаметрах построены три окружности. Известно, что они попарно пересекаются. Пусть C₁ — более удаленная от вершины C точка пересечения окружностей, построенных на медианах AM₁ и BM₂. Точки A₁ и B₁ определяются аналогично. Докажите, что прямые АА₁, ВВ₁ и СС₁ пересекаются в одной точке.

5. Докажите, что у любого выпуклого многогранника найдутся три ребра, из которых можно составить треугольник.

6. К двум окружностям w₁ и w₂, пересекающимся в точках А и В, проведена их общая касательная CD (C и D — точки касания соответственно, точка B ближе к прямой CD, чем А). Прямая, проходящая через А, вторично пересекает w₁ и w₂ в точках К и L соответственно (A лежит между K и L). Прямые KC и LD пересекаются в точке p. Докажите, что РВ — симедиана треугольника KpL (прямая, симметричная медиане относительно биссектрисы).

Олимпиадные задания по математике для учащихся 1-11 классов с решением и ответами:

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Abcd четырехугольник вписанный в окружность m точка пересечения его диагоналей

Видео:Вписанный в окружность четырёхугольник.Скачать

Разделы

Видео:Геометрия Четырёхугольник ABCD со сторонами AB = 2 и CD = 5 вписан в окружность. Диагонали AC и BDСкачать

Дополнительно

Задача по математике — 6838

Дан треугольник со сторонами 25, 25 и 48.
а) Докажите, что он тупоугольный.
б) Найдите расстояние между центрами его вписанной и описанной окружностей.

Задача по математике — 6839

Длины сторон $AB$, $AD$, $BC$ и $CD$ выпуклого четырёхугольника $ABCD$ в указанном порядке образуют арифметическую прогрессию.
а) Докажите, что в этот четырёхугольник можно вписать окружность.
б) Найдите радиус этой окружности, если известно, что $AB=6$, $AD=8$, $BC=10$, $CD=12$ и $BD=BC$.

Задача по математике — 6840

Дан выпуклый четырёхугольник $ABCD$ со сторонами $AB=3$, $BC=CD=5$, $AD=8$ и диагональю $AC=7$.
а) Докажите, что около него можно описать окружность.
б) Найдите диагональ $BD$.

Задача по математике — 6841

Сторона $AC$ треугольника $ABC$ больше стороны $AB$. Вписанная в треугольник окружность касается стороны $BC$ в точке $M$, а вневписанная — в точке $N$.
а) Докажите, что $MN=AC-AB$.
б) Найдите расстояние между центрами указанных окружностей, если сумма их радиусов равна 24, а $MN=10$.

Задача по математике — 6842

Диагонали $AC$ и $BD$ выпуклого четырёхугольника $ABCD$ перпендикулярны.
а) Докажите, что $AB^+CD^=BC^+AD^$.
б) Известно, что в этот четырёхугольник можно вписать окружность. Найдите её радиус, если $BC=8$, $CD=12$, $angle BAD=150^$.

Задача по математике — 6843

Точка $M$ — середина гипотенузы $AB$ прямоугольного треугольника $ABC$. На отрезке $CM$ как на диаметре построена окружность.
а) Докажите, что она проходит через середины катетов.
б) $AP$ и $BQ$ — касательные к этой окружности ($P$ и $Q$ — точки касания). Найдите отношение $AP:BQ$, если известно, что $tgangle ABC=2$.

Задача по математике — 6844

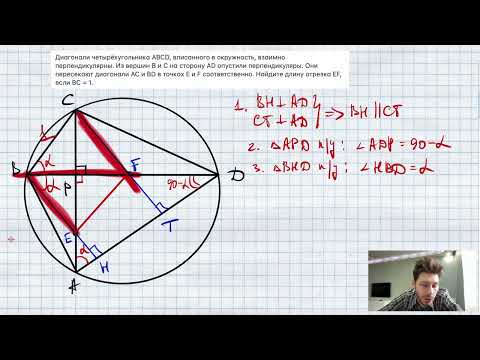
Четырёхугольник $ABCD$ с перпендикулярными диагоналями $AC$ и $BD$ вписан в окружность.
а) Докажите, что прямая, проходящая через точку пересечения диагоналей четырёхугольника перпендикулярно стороне $BC$, делит пополам сторону $AD$.
б) Найдите стороны четырёхугольника $ABCD$, если известно, что $AC=84$, $BD=77$, а диаметр окружности равен 85.

Задача по математике — 6845

Отрезок $CD$ — биссектриса треугольника $ABC$. Окружность, проходящая через точки $C$ и $D$ касается стороны $AB$ и пересекает стороны $AC$ и $BC$ в точках $M$ и $N$ соответственно.
а) Докажите, что $MNparallel AB$.
б) Найдите $MN$, если известно, что $AD=2$, $BD=4$ и $AM=1$.

Задача по математике — 6846

Основание и боковая сторона равнобедренного треугольника равны 26 и 38 соответственно.
а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.
б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.

Задача по математике — 6847

В окружность вписан четырёхугольник с тремя равными сторонами.
а) Докажите, что в этом четырёхугольнике есть параллельные стороны.
б) Найдите диагонали четырёхугольника, если известно, что радиус окружности равен 25, а каждая из трёх равных сторон четырёхугольника равна 30.

Задача по математике — 6848

В выпуклом четырёхугольнике $ABCD$ известно, что $cosangle ABC=-cosangle ADC$.
а) Докажите, что $angle ABD=angle ACD$.
б) Найдите радиус окружности, описанной около этого четырёхугольника, если известно, что $angle ACB=30^$, $BC=6$, а высоты треугольников $ABD$ и $CBD$, проведённые из вершины $B$, равны.

Задача по математике — 6849

Окружность с центром $O$, вписанная в треугольник $ABC$, касается сторон $AB$ и $AC$ в точках $M$ и $N$ соответственно, $AH$ — высота треугольника. Прямые $MN$ и $BC$ пересекаются в точке $K$.
а) Докажите, что $angle MKB=angle OAH$.
б) Найдите $AK$, если известно, что $angle ABC=77^$, $angle ACB=17^$, а отрезок, соединяющий точку $H$ с серединой $MN$, равен 8.

Задача по математике — 6850

На основаниях $AD$ и $BC$ трапеции $ABCD$ построены квадраты $ADEF$ и $BCGH$, расположенные вне трапеции.
а) Докажите, что прямая $FG$ проходит через точку пересечения диагоналей трапеции.
б) Прямая, проходящая через центры квадратов, пересекает основание $BC$ в точке $M$. Найдите $BM$, если известно, что $BC=20$, $ACperp BD$ и $BD:AC=3:2$.

Задача по математике — 6851

Окружность, вписанная в равнобедренную трапецию $ABCD$, касается боковых сторон $AB$ и $CD$ в точках $M$ и $N$ соответственно. Отрезок $AN$ пересекает окружность в точке $K$, а луч $MK$ пересекает основание $AD$ в точке $L$.
а) Докажите, что треугольник $AKL$ подобен треугольнику $MAL$.
б) Найдите отношение $AL:LD$.

Задача по математике — 6852

$AA_$, $BB_$ и $CC_$ — высоты остроугольного треугольника $ABC$ с углом $45^$ при вершине $C$.
а) Докажите, что треугольник $A_B_C_$ прямоугольный.
б) Найдите отношение, в котором высота $AA_$ делит отрезок $B_C_$, если известно, $BC=2B_C_$.

🎦 Видео

Решение задачи 25 из ОГЭ по математике 9 классСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Геометрия 11 класс. Вписанный четырехугольникСкачать

Геометрия Диагонали четырёхугольника ABCD, вершины которого расположены на окружности, пересекаютсяСкачать