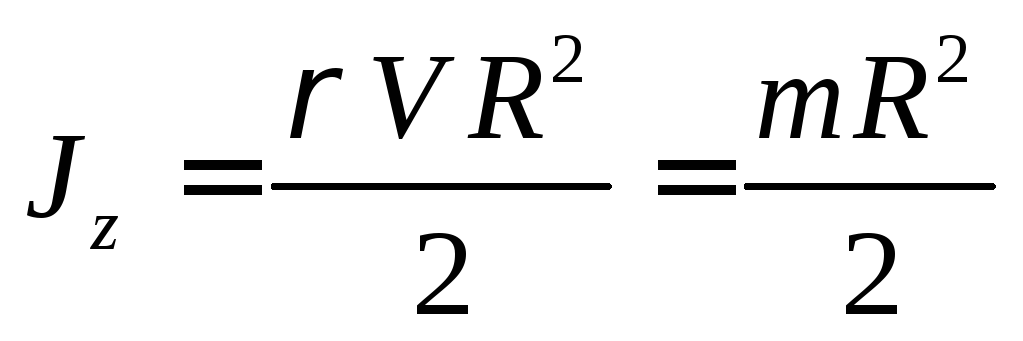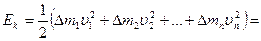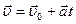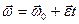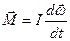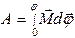В настоящее время является общепризнанным, что получить информацию о топологии (геометрии) реального глобального пространства Вселенной (глобального пространства) и о динамике изменения основных параметров этой топологии (геометрии), к которым относится текущий радиус Вселенной, мы можем только из астрономических наблюдений. Я полагаю и берусь доказать следующее: Во-первых, собранные к настоящему времени данные астрономических наблюдений однозначно указывают на то, что топология глобального трехмерного пространства Вселенной (глобального трехмерного пространства) является топологией трехмерной сферы, либо она является трехмерной топологией, которая является подмножеством сферы большей размерности. Во-вторых, радиус указанной трехмерной сферы (радиус Вселенной) или радиус указанной сферы большей размерности (больше трех) всегда растет со скоростью света в вакууме. Более того, сама скорость света в вакууме является величиной определяемой скоростью роста радиуса Вселенной. Более того, скорость роста радиуса указанной трехмерной сферы (радиуса Вселенной), как и равная ей скорость света в вакууме являются величинами неизменными, или по крайней мере чрезвычайно высокостабильными и не меняются буквально с первых минут после Большого взрыва или после начала очередного цикла расширения Вселенной.
Чтобы сразу заинтриговать достаточно искушенного читателя, замечу, что для предлагаемой модели постоянная Хаббла всегда равна скорости света в вакууме деленной на расстояние до максимально удаленных наблюдаемых объектов Вселенной. При этом время существования (расширения) Вселенной автоматически равно расстоянию до максимально удаленных наблюдаемых объектов Вселенной деленному на скорость света в вакууме, то есть автоматически совпадает с величиной обратной постоянной Хаббла. Интересно, что в критикуемой мной модели евклидова (плоского) расширяющегося пространства Вселенной (Лямбда-CDM теории) время существования (расширения) Вселенной также оценивается, как величина обратная постоянной Хаббла. Однако причина такой оценки в критикуемой мной модели евклидова (плоского) расширяющегося пространства Вселенной опирается не на математическую модель этой теории, на которую в качестве этой причины ошибочно указывают некоторые авторы, а на тот факт, что измеренное астрономами расстояние до максимально удаленных объектов во Вселенной в световых годах деленное на скорость света действительно оказалось примерно равно времени существования (расширения) Вселенной. Только в критикуемой модели евклидова (плоского) пространства такое совпадение расценивается как случайное для настоящего момента (периода) времени, а в предлагаемой мной модели это выполняется во Вселенной всегда и автоматически. Если посмотреть любой график расширения Вселенной для этой критикуемой мной модели, то легко понять и заметить, что это равенство времени существования (расширения) Вселенной и величины обратной постоянной Хаббла никогда в истории Вселенной не выполнялось, кроме настоящего времени.
При этом, в предлагаемой мной модели, при условии что радиус Вселенной растет со скоростью света, расстояние до максимально удаленных наблюдаемых объектов Вселенной автоматически равно радиусу Вселенной (радиусу соответствующей трехмерной сферы, либо радиусу соответствующей шестимерной или пятимерной сферы, подмножествами которых являются соответственно обычный кубический тор Клиффорда или сферический квази-кубический тор Клиффорда). Но в предлагаемой мной модели не обязательно выполнения равенства радиуса Вселенной расстоянию до максимально удаленных наблюдаемых объектов Вселенной, как необходимого условия для автоматического выполнения указанного равенства времени существования (расширения) Вселенной и расстояния до максимально удаленных наблюдаемых объектов Вселенной деленного на скорость света в вакууме. Обязательным необходимым условием для выполнения данного равенства является постоянство скорости роста радиуса Вселенной. Дополнительно предполагается только, что скорость роста радиуса Вселенной больше, чем скорость света деленная на число пи. Это необходимо, чтобы мы не могли видеть одни и те же Объекты Вселенной и в прямом направлении и в противоположном, но с другой стороны. Равенство же скорости роста радиуса Вселенной скорости света в вакууме устанавливается из иных наблюдений, о которых я расскажу несколько ниже.
Тот, кто действительно интересуется наукой, и у кого хватило ума или воображения, чтобы усечь разницу между моей моделью и официозной моделью евклидова (плоского) плоского пространства, дальше просто не оторвется и не отвертится от полного прочтения настоящей статьи.
Предлагаемая мной модель имеет еще одно важное преимущество. В предлагаемой мной модели космологическое красное смещение в спектре наблюдаемых сейчас объектов Вселенной определяется только отношением радиуса Вселенной в настоящий момент (сейчас) к радиусу Вселенной в момент излучения этими объектами света, который мы сейчас наблюдаем. Сразу оговорюсь, что величина, которую я называю здесь красным смещением, для удобства описания является отношением длины волны в наблюдаемой линии спектра (например линии водорода) наблюдаемого отдаленного объекта Вселенной, к стандартной (измеренной для близких лабораторных объектов) длине волны той же линии (в выбранном примере — линии водорода). Это на единицу больше, чем красное смещение по учебникам и справочникам.
То есть, при условии постоянной скорости увеличения радиуса Вселенной, в предлагаемой мной модели космологическое красное смещение в спектре наблюдаемых объектов Вселенной равно отношению настоящего (на настоящий момент времени (сегодня)) времени существования Вселенной ко времени существования Вселенной в момент излучения ими света, который мы наблюдаем сейчас. То есть, при условии постоянной скорости роста радиуса Вселенной, в предлагаемой мной модели указанное отношение времен и соответствующее космологическое красное смещение в спектре наблюдаемых объектов равно отношению существующего в настоящий момент расстояния до максимально удаленных от Земли и видимых с Земли объектов Вселенной к расстоянию до максимально удаленных от Земли и видимых с Земли объектов Вселенной в момент излучения ими света. При условии постоянной скорости роста радиуса Вселенной, зная скорость роста радиуса Вселенной, непосредственно по красному смещению в их спектрах мы можем определить расстояния между Землей и этими объектами сегодня. В предлагаемой модели это расстояние определяется следующей простейшей формулой
L=S*T*(1-1/K)
где
L — расстояния между Землей и наблюдаемым объектом Вселенной, для которого определяется космологическое красное смещение;
S — скорость роста радиуса Вселенной (которая равна, как мы докажем далее
равна С — скорости света в вакууме;
T — возраст Вселенной в настоящее время;
K — красное смещение, определяемое как л0/л, где л0 — длина длины волны в наблюдаемой линии спектра (например линии водорода) наблюдаемого отдаленного объекта Вселенной, л — стандартная (измеренная для близких лабораторных объектов) длина волны той же линии (в выбранном примере — линии водорода).
Определение расстояния до удаленных объектов Вселенной по их светимости и приравнивание его к расстоянию, полученному с помощью данной формулы по космологическому красному смещению в рамках данной предлагаемой мной модели приводит к выводу о том, что S — скорость роста радиуса Вселенной равна С — скорости света в вакууме.
Хотя я полагаю, что Фридмановская модель расширения Вселенной содержит много существенных ошибок вследствие соответствующих ошибок ОТО (общей теории относительности), я имею в виду ошибочное десятое уравнение Эйнштейна. Эту ошибку не исправило, а только запутало введение космологической постоянной лямбда. Тем не менее и в этой модели есть решение для сферической модели Вселенной, в рамках которой Вселенная всегда расширяется с постоянной скоростью. Главной ошибкой в этой модели является введение критической плотности, но об этом подробнее во введении к другой моей статье «Геометрия Вселенной и главная проблема физики 30».
Чтобы еще раз окончательно заинтриговать читателя я, пожалуй, проведу одну нескромную аналогию. Предлагаемая мной модель топологии и динамики Вселенной настолько же проще, удобнее и правильнее, чем критикуемая мной модель евклидова (плоского) пространства Вселенной (Лямбда-CDM теория), насколько гелиоцентрическая модель Коперника проще, удобнее и правильнее, чем геоцентрическая модель Вселенной, которою еще два века с таким упорством отстаивала церковь и инквизиция, преследовавшая Галилея и других сторонников модели Коперника. Впрочем, современная инквизиция отстаивает свою модель (и свою кормушку) не менее ожесточенно, хотя посадить меня пока не пыталась. Для этого теперь есть не менее эффективные методы информационной изоляции.
Конечно же топология реального глобального пространства может несколько отличаться от предлагаемой модели, но в любом случае она топологически близка к этой модели и должна ею аппроксимироваться.
Трехмерными топологиями, которые являются подмножествами вышеуказанных сфер, размерности которых больше трех, являются следующие топологии: Во-первых, такой топологией является обычный трехмерный кубический (R1=R2=R3) тор Клиффорда, свободно вписанный в шестимерное евклидово пространство (S1*S1*S1) (T3-R6). При равенстве друг другу всех трех радиусов R1=R2=R3 трех образующих окружностей (первой, второй и третьей) обычного трехмерного тора Клиффорда он называется кубическим тором Клиффорда и является подмножеством шестимерной сферы, радиус которой равен корень квадратный из трех умножить на R1. Во-вторых, указанной топологией является сферический квази-кубический (R1=R2) трехмерный тор Клиффорда, свободно вписанный в пятимерное евклидово пространство (S1*S2) (T3-R5). При равенстве друг другу радиуса R1 образующей окружности и радиуса R2 образующей двумерной сферы сферического трехмерного тора Клиффорда он называется сферическим квази-кубическим тором Клиффорда и является подмножеством пятимерной сферы с радиусом равным корень квадратный из двух умножить на R1.
В пользу предлагаемой мной модели говорят следующие собранные к настоящему времени данные астрономических наблюдений:
Во-первых, самые удаленные из наблюдаемых галактик, находятся от нас примерно на почти одинаковом расстоянии по всем направлениям, почти равном в световых годах возрасту Вселенной, и удаляются от нас примерно с одной и той же скоростью близкой к скорости света в вакууме. Действительно, согласно современным представлениям наиболее удаленный от нас наблюдаемый объект во Вселенной — галактика GN-z11 — расположен на расстоянии от нас около 13,4 миллиардов световых лет. Почти на таком же расстоянии расположены от нас и другие максимально удаленные от нас объекты по всем направлениям в пространстве. Возраст Вселенной оценивается астрофизиками в величину примерно 13,8 миллиардов лет. Следовательно, средняя скорость удаления от нас этого объекта и других максимально удаленных наблюдаемых объектов по всем другим направлениям в пространстве близка к скорости света. С высочайшей степенью вероятности, мы не проживаем случайно именно в то время, когда средняя скорость удаления от нас этих максимально удаленных наблюдаемых объектов по всем направлениям в пространстве почти совпала со скоростью света — вполне определенной и неизменной физической константой. Следовательно, наиболее вероятно, что скорость удаления от нас этих максимально удаленных наблюдаемых объектов по всем направлениям в пространстве всегда была близка к скорости света. Поскольку Земля не является центром Вселенной, факт удаления от Земли максимально удаленных наблюдаемых объектов по всем направлениям в пространстве с одинаковой скоростью — со скоростью света в моделях с расширяющимся пространством Вселенной не может быть объяснен для евклидова (плоского) трехмерного пространства без двух крайне надуманных допущений: Первым таким допущением является допущение об однородном расширении этого евклидова (плоского) трехмерного пространства, предполагающее экспоненциально растущую скорость увеличения радиуса трехмерного шара, которым является наша расширяющаяся Вселенная в предположении о евклидовости ее трехмерного пространства. Вторым таким допущением является допущение о достаточной удаленности Земли от границы этого шара.
В то же время, факт удаления от Земли максимально удаленных наблюдаемых объектов по всем направлениям в пространстве с одинаковой скоростью — со скоростью света в моделях с расширяющимся пространством Вселенной легко объясняется для пространства со сферической топологией либо с трехмерной топологией, которая является подмножеством сферы большей размерности (больше трех), без использования подобных сложных допущений . Для этого достаточно предположить, что радиус соответствующей сферы (радиус Вселенной) растет с постоянной скоростью.
Однако вышеуказанные допущения для модели пространства Вселенной в виде евклидова (плоского) трехмерного пространства делают практически необъяснимыми для этой модели другие наблюдаемые явления, поскольку для подобных объяснений требуются уже намного более надуманные допущения, которые представляются буквально уже просто высосанными из пальца. Такие еще более надуманные допущения для модели евклидова (плоского) трехмерного пространства Вселенной необходимы для объяснения того факта, что самые удаленные из наблюдаемых галактик, находятся от нас примерно на одинаковом расстоянии по всем направлениям, равном в световых годах возрасту Вселенной. В случае же сферической топологии пространства Вселенной для объяснения указанного факта достаточно предположить, что радиус соответствующей сферы (радиус Вселенной) растет с постоянной скоростью. Далее я подробно расскажу об указанных допущениях для моделей пространства Вселенной в виде евклидова (плоского) трехмерного пространства:
Сначала для такого евклидова (плоского) трехмерного пространства Вселенной рассмотрим случай, когда граница видимости объектов Вселенной удаляющихся от нас вследствие расширения пространства находится от нас на расстояниях меньших чем минимальное расстояние до границы трехмерного пространственного шара, являющегося нашей Вселенной (границы Вселенной). В этом случае, вследствие экспоненциального роста скорости этой границы Вселенной и экспоненциального роста скорости удаления от Земли любых достаточно удаленных объектов Вселенной, мы не смогли бы видеть свет от объектов Вселенной, излученный ими на ранних стадиях существования Вселенной (временная отсечка), в том числе мы не смогли бы видеть свет (радиоволны) реликтового излучения (микроволнового космического фона), поскольку это свет от всех объектов Вселенной при такой евклидовой (плоской) трехмерной топологии давно уже должен был пройти через Землю на тех стадиях расширения Вселенной, когда скорость удаления от Земли любых точек границы Вселенной (границы трехмерного пространственного шара, являющегося нашей Вселенной) была намного меньше скорости света.
Для объяснения наблюдаемости реликтового излучения и наблюдаемости излучения первых древнейших галактик (при условии экспоненциально растущей скорости увеличения радиуса трехмерного евклидова (плоского) шарообразного пространства Вселенной), сторонники современной теории евклидова (плоского) трехмерного пространства Вселенной (Лямбда-CDM теории) прибегают к чрезвычайно крайне надуманному объяснению, основанному на предположении о том, что ранее скорость увеличения радиуса трехмерного шарообразного пространства Вселенной была экспоненциально или гиперболически убывающей неизвестно сколько по времени (подгоняйте как угодно), а в первые сотни тысяч лет после возникновения Вселенной имело место гипер-инфляционное расширения, которое продолжалось неизвестно сколько по времени с весьма приблизительными параметрами (подгоняйте как угодно), а средняя скорость расширения Вселенной, как и скорость удаления от нас всех максимально удаленных наблюдаемых объектов по всем направлениям в пространстве, в настоящее время случайно оказались примерно равными скорости света.
А теперь для такого евклидова (плоского) трехмерного пространства Вселенной рассмотрим случай, когда граница видимости объектов Вселенной удаляющихся от нас вследствие указанного однородного расширения пространства находится от нас на расстояниях больших, чем минимальное расстояние до границы трехмерного пространственного шара, являющегося нашей Вселенной (границы Вселенной). В этом случае, в направлении минимального расстояния до границы трехмерного пространственного шара, являющегося нашей Вселенной, мы можем увидеть объекты, находящиеся на границе Вселенной (на границе этого шара), а далее этой границы мы не увидим ничего. Кроме того в этом направлении мы ни при каких обстоятельствах не увидим реликтового излучения, поскольку оно в таком случае должно было давно уже пройти через Землю. В противоположном направлении мы сможем увидеть объекты, расположенные на значительно больших расстояниях, а потому количество таких наблюдаемых объектов на небе в этом направлении максимального расстояния до границы Вселенной должно быть значительно больше, чем в направлении минимального расстояния до границы Вселенной. Однако, мы реально наблюдаем примерно одинаковое количество объектов одинаковой природы (звезд соответствующих типов, квазаров, галактик, скоплений галактик, сверхскоплений галактик, интенсивности и температуры реликтового излучения, и т.п.) во Вселенной во всех направлениях.
Несколько слов по поводу так называемой «измеренной» сторонниками евклидова (плоского) пространства Вселенной скорости расширения Вселенной, которая заявляется равной 73.8 километров в секунду на каждые 3.26 миллионов световых лет (мегапарсек): Отсюда следует, что пространство и несомые им иные материальные объекты) на расстоянии от нас в световых годах равном возрасту Вселенной удаляются от нас со скоростью примерно 312405 километров в секунду. Не смущает подозрительная близость этой величины к скорости света в вакууме? Очевидно, что мы сталкиваемся с откровенной подгонкой под известный вышеупомянутый результат других наблюдений, согласно которому скорость удаления от нас всех максимально удаленных наблюдаемых объектов по всем направлениям в пространстве близка к скорости света. Очевидно, что сторонники евклидова (плоского) пространства Вселенной намеренно или по недомыслию забывают, что мы видим эти максимально удаленные объекты такими, какими они были на заре существования Вселенной, то есть в возрасте около 400 000 лет, и свет который приходит от них к нам был излучен именно тогда, то есть более 13,4 миллиардов лет назад. Следовательно, этот свет (фотоны) никогда не были удалены от Земли более чем на 400 000 световых лет, но вследствие расширения пространства его путешествие к нам растянулось примерно на 13,4 миллиардов лет. Но теперь следует вспомнить, что расстояние от нас до этих несомых пространством объектов (вместе с радиусом (размерами) самого пространства) согласно указанной теории однородного расширения евклидова (плоского) пространства постоянно экспоненциально растет во времени, а само это расширение пространства является однородным.
Рассмотрим теперь для указанной теории евклидова (плоского) пространства первый случай, когда расстояние от нас до указанных максимально удаленных объектов было в 2 раза меньше, чем теперь, скорость их удаления вместе с несущим их пространством также была в 2 раза меньше, чем в настоящее время, то есть в 2 раза меньше скорости света в вакууме. То есть пространство на максимальном расстоянии от этих объектов до нас расширялось тогда в 2 раза медленнее скорости света, а до этого оно расширялось еще намного медленнее. Вследствие того, что в теории евклидова (плоского) пространства расширение Вселенной (границ Вселенной и расстояния между объектами Вселенной) происходит экспоненциально во времени, рассматриваемый случай имел место всего 13,8*(-ln(1/(2)))=13,8*(0,7)=9,66 миллиардов лет назад. Расстояние между положениями Земли сейчас положением Земли (ранних объектов соответствующих Солнечной системе) 9,66 миллиардов лет назад составляет не более 13,8/2=6,9 миллиардов световых лет для случая, когда Земля находится на самой границе Вселенной. Это означает, что даже свет излученный 9,66 миллиардов лет назад объектами, которые тогда 9,66 миллиардов лет назад находились на расстоянии от Земли (ранних объектов соответствующих Солнечной системе) равном 9,66-6,9=2,76 миллиардов световых лет, к настоящему времени навсегда пролетел и безвозвратно покинул Землю (ранние объекты соответствующие Солнечной системе). А это почти половина тогдашнего радиуса Вселенной. Свет же излученный с этих расстояний и даже несколько больших расстояний ранее заведомо навсегда покинул Землю еще раньше, даже если раньше Вселенная расширялась иначе. Легко проверить, что эта аппроксимация в 2,76 миллиардов световых лет приблизительно выполняется для любого положения (расстояния) Земли от центра Вселенной. А это уже означает, что Земля (ранние объекты соответствующие Солнечной системе) должна находиться практически в центре Вселенной, чтобы мы могли видеть реликтовое излучение примерно одинаковым со всех направлений, каковым мы его и видим. То же самое касается и других максимально удаленных от Земли объектов (древнейших галактик, гигантских древних квазаров, и т.п.). Если же Земля находится на самом краю или почти на самом краю Вселенной, это означает, что мы будем видеть реликтовое излучение и других древнейшие объекты только в направлении на центр Вселенной и только в области с максимальным коническим углом 150 градусов. Если же Земля находится посередине между краем и центром Вселенной, это означает, что мы не будем видеть реликтового излучения и других максимально удаленных древнейших объектов в направлении противоположном направлению на центр Вселенной в области с минимальным коническим углом около 5 градусов; а в угловом распределении интенсивности реликтового излучения по другим направлениям и в уловом распределении количества древнейших объектов Вселенной по другим направлениям будет наблюдаться существенная анизотропия. Однако реально мы видим практически одинаковое изотропное распределение интенсивности реликтового излучения и одинаковое изотропное распределение количества древнейших объектов Вселенной по углу наблюдения. Следовательно, пространство Вселенной не является евклидовым (плоским).
Рассмотрим теперь для указанной теории евклидова (плоского) пространства второй случай, когда расстояние от нас до указанных максимально удаленных объектов было в 2,5 раза меньше, чем теперь, скорость их удаления вместе с несущим их пространством также была в 2,5 раза меньше, чем в настоящее время, то есть в 2,5 раза меньше скорости света в вакууме. То есть пространство на максимальном расстоянии от этих объектов до нас расширялось тогда в 2,5 раза медленнее скорости света, а до этого оно расширялось еще намного медленнее. Вследствие того, что в теории евклидова (плоского) пространства расширение Вселенной (границ Вселенной и расстояния между объектами Вселенной) происходит экспоненциально во времени, рассматриваемый случай имел место всего 13,8*(-ln(1/(2,5)))=13,8*(0,92)=12,7 миллиардов лет назад. Расстояние между положениями Земли сейчас положением Земли (ранних объектов соответствующих Солнечной системе) 12,7 миллиардов лет назад составляет 13,8*(1-1/2,5)=8,28 миллиардов световых лет. Это означает, что даже свет излученный 12,7 миллиардов лет назад объектами, которые тогда 12,7 миллиардов лет назад находились на расстоянии от Земли (ранних объектов соответствующих Солнечной системе) равном 12,7-8,28=4,42 миллиардов световых лет, к настоящему времени навсегда пролетел и безвозвратно покинул Землю (ранние объекты соответствующие Солнечной системе). А это 80 процентов тогдашнего радиуса Вселенной составлявшего 5,52 миллиардов световых лет. А это уже означает, что Земля (ранние объекты соответствующие Солнечной системе) должна находиться буквально в центре Вселенной, чтобы мы могли видеть реликтовое излучение одинаковым со всех направлений, и почти в центре Вселенной, чтобы среди этих направлений не было огромного пустого пятна, от которого реликтовое излучение не поступает совсем. Если Земля находится посередине между краем и центром Вселенной, это означает, что мы не будем видеть реликтового излучения и других максимально удаленных древнейших объектов в направлении противоположном направлению на центр Вселенной в области с минимальным коническим углом около 110 градусов. То же самое касается и других максимально удаленных от Земли объектов (древнейших галактик, гигантских древних квазаров, и т.п.).
(Чтобы понять тенденцию рассмотрим также третий случай, когда расстояние от нас до указанных максимально удаленных объектов было в 1,5 раза меньше, чем теперь, скорость их удаления вместе с несущим их пространством также была в 1,5 раза меньшие, чем в настоящее время, то есть в 1,5 раза меньше скорости света в вакууме. То есть пространство на максимальном расстоянии от этих объектов до нас расширялось тогда в 1,5 раза медленнее скорости света, а до этого оно расширялось еще намного медленнее. Вследствие того, что в теории евклидова (плоского) пространства расширение Вселенной (границ Вселенной и расстояния между объектами Вселенной) происходит экспоненциально во времени, рассматриваемый случай имел место всего 13,8*(-ln(1/(1,5)))=13,8*(0,41)=5,66 миллиардов лет назад. То есть между первым и вторым случаем прошло 4 миллиарда лет. Расстояние в положении Земли между этими событиями равно 13,8* (0,66-0,5)= 2,208 миллиардов световых лет. Это означает, что даже свет излученный 9,66 миллиардов лет назад объектами, которые тогда 9,66 миллиардов лет назад находились на расстоянии от Земли (ранних объектов соответствующих Солнечной системе) равном 4-2,208=1,792 миллиардов световых лет, еще 5,66 миллиардов лет назад навсегда пролетел и безвозвратно покинул Землю (ранние объекты соответствующие Солнечной системе).)
Это означает, что свет излученный на ранних стадиях существования Вселенной давно, много миллиардов лет назад должен был безвозвратно пролететь через Землю, и мы при условии евклидова (плоского) пространства Вселенной не могли бы видеть ни реликтового излучения, ни первых древнейших галактик, ни древних гигантских квазаров по крайней мере почти равномерно по всем направлениям. Однако мы наблюдаем все эти объекты именно так. Очевидно, что сторонники евклидова (плоского) пространства Вселенной не вполне понимают: что и как они измеряют. Что бы избежать указанных противоречий, они придумывают истории о том, что Вселенная экспоненциально расширяется с современными параметрами только последние 4 миллиарда лет (всего несколько лет назад считали, что 6-7 миллиардов лет), а до этого около скорость ее расширения была почти постоянной, а в самом начале Вселенная инфляционно расширялась с немыслимыми скоростями за 10 в -35 степени секунды ее размеры (радиус) увеличились от 0 до нескольких миллиардов световых лет, и постоянно придумывают прочие сложности по мере того, как растущая точность измерений уничтожает ранее нагроможденные навороты. Прогнозирую, что лет через пять или раньше упомянутые последние 4 миллиарда лет экспоненциального расширения превратятся уже в 2-3 миллиарда лет. При этом они не любят вспоминать о том, что однородное расширение евклидова (плоского) пространства уже само по себе чисто математически порождает экспоненциальное разбегание границ и объектов Вселенной. Лучше, конечно, получить Нобелевские премии за открытие экспоненциального расширения. А с экспонентами шутки плохи, особенно когда показатель степени становится отрицательным. Что бы заглянуть во времена, когда размеры Вселенной были в 3 раза меньше нынешних, придется «заглянуть» во времена до «Большого взрыва», согласно формуле на 13,8*(-ln(1/(3)))=13,8*(1,2)=16,56 миллиардов лет назад. Что конечно же делает непригодными ранее использованные параметры параметры однородного расширения, а заодно и соответствующей экспоненты. Вообще ситуация с теорией евклидова (плоского) пространства Вселенной (Лямбда-CDM теорией) все больше напоминает ситуацию с инквизицией пятисотлетней давности. Как и тогда современная научная инквизиция по всему миру гасит любых современных Коперников и Галилеев, полностью вычищая их из информационного пространства. Спасибо что в наши дни за правду хотя бы не сажают, хотя с нынешними тенденциями и до этого скоро дойдет. Я конечно же говорю о серьезных альтернативных официозным теориях, а не о глупом благонамеренном бреде, который по сути никому не угрожает, и который благополучно печатают даже в официозных толстых журналах, наверное для того, чтобы выпятить собственное превосходство. Та же ситуация и с серьезными альтернативами ОТО (общей теории относительности).
Во-вторых, за все время наблюдений ни одна из наблюдаемых далеких галактик не скрылась из вида, и, по-видимому, в поле возможной видимости не появляется новых галактик, что указывает на высокую степень постоянства скорости их удаления за время современных астрономических наблюдений. Не изменяется и видимая область поверхности последнего рассеяния — космическая карта реликтового излучения — карта флуктуаций космического микроволнового фона. Это подтверждает вывод о том, что скорость удаления от нас максимально удаленных объектов (галактик и т.п., поверхности последнего рассеяния) по всем направлениям в пространстве за время наблюдений является постоянной, и всегда была близка к скорости света.
Кроме того, наблюдения за красным смещением достаточно далеких галактик и скоплений и сверхскоплений галактик, показывают высочайшую степень постоянства этого красного смещения, связанного с глобальным расширением пространства, то есть с учетом поправки на их иное относительное движение. Таким образом эти наблюдения подтверждают высочайшую степень постоянства скорости их глобального (связанного с глобальным расширением пространства) удаления от Земли.
В-третьих, на крупных масштабах соответствующих примерно десяткам сверхскоплений галактик, пространство Вселенной наблюдается, как достаточно однородная структура, за малым количеством наблюдаемых исключений, проявляющих себя, как указание на наличие во Вселенной одной или нескольких выделенных осей (подробнее об этом немного ниже).
В-четвертых, априори Земля не является центром Вселенной, что подтверждает также и третий факт, следовательно, для любой точки (объекта) во Вселенной выполняется то же правило, что и для Земли, а именно: наиболее удаленные от любого объекта по всем направлениям другие видимые объекты во Вселенной находятся от него на расстоянии немного меньшем (или равным), чем 13,8 миллиардов световых лет (на расстоянии Хаббловской длины) и удаляются от него со скоростью немного меньшей (или равной) скорости света.
Уже первые четыре вышеперечисленных факта (перечисленные после слов: во-первых; во-вторых; в-третьих; в-четвертых) практически невозможно объяснить никакой иной геометрией глобального пространства Вселенной, кроме его геометрии именно в виде трехмерной гиперсферы, либо геометрией близкой к ней, включая геометрию недеформированного (либо мало-деформированного) трехмерного гипертора, у которого радиус третьей образующей окружности много больше как радиуса второй образующей окружности, так и радиуса третьей образующей окружности. Также геометрией близкой к геометрии трехмерной гиперсферы является геометрия сферически деформированного трехмерного гипертора, у которого радиус третьей образующей окружности много больше как радиуса второй образующей окружности, так и радиуса первой образующей окружности. В число близких по геометрии поверхностей необходимо включить также трехмерные поверхности, являющиеся подмножеством гиперсфер более высоких размерностей. К таким трехмерным поверхностям относится обычный трехмерный тор Клиффорда, свободно вписанный в шестимерное евклидово пространство (T3-R6), поскольку при равенстве друг другу всех трех радиусов R1=R2=R3 его образующих окружностей (первой, второй и третьей), он является подмножеством шестимерной сферы с радиусом равным корень квадратный из трех умножить на R1. К таким трехмерным поверхностям относится сферический трехмерный тор Клиффорда, свободно вписанный в пятимерное евклидово пространство (T3-R5), поскольку при равенстве друг другу радиуса R1 его образующей окружности радиусу R2 его образующей двумерной сферы, он является подмножеством пятимерной сферы с радиусом равным корень квадратный из двух умножить на R1.
При этом радиус такой трехмерной гиперсферы (глобального пространства Вселенной), в том числе трехмерной гиперсферы, которой мы аппроксимируем в соответствующей глобальной части наш трехмерный гипертор, или радиус соответствующей пятимерной или шестимерной сферы для указанных торов Клиффорда должен расти со временем согласно формуле:
где Tглоб. — глобальное время существования Вселенной, а C — скорость света в вакууме, Rглоб. — радиус нашей трехмерной (или пятимерной или шестимерной для соответствующих торов Клиффорда) гиперсферы или квази-гиперсферы (глобального пространства Вселенной), A -соответствующий постоянный численный коэффициент, который в принципе может иметь значения от нуля, но больше нуля, до числа пи (3,1415. ). Максимум равный числу пи (3,1415. ) имеет место, поскольку наблюдаемое пространство не простирается далее половины длины максимально большой (меридианной) окружности на сфере, так как мы не наблюдаем один и тот же удаленный (почти максимально) объект по разным направлениям. При этом максимально удаленные от нас объекты Вселенной доступные нашему наблюдению удаляются от нас с постоянной скоростью равной скорости света в вакууме. Поэтому свет от таких объектов может идти к нам бесконечно долго, поскольку движение к нам света, распространяющегося в пространстве со скоростью света, компенсируется расширением самого пространства, вследствие которого эти объекты удаляются от нас тоже со скоростью света. Таким образом свет, поступающий к нам от таких объектов шел к нам все время существования Вселенной равное Tглоб. За это время расстояние от нас до этих объектов вследствие увеличения Rглоб. и соответствующего увеличения дуги распространения света на соответствующей расширяющейся сфере, являющейся пространством нашей Вселенной, увеличилось до значений равных Tглоб.*C, то есть стало равно Rглоб.*A. Следовательно, максимально удаленные от нас объекты, которые мы можем видеть лежат от нас на угловом расстоянии в радианах равном A. Этот угол отсчитывается от луча проходящего через Землю и исходящего из геометрического центра соответствующей сферы содержащей или являющейся нашим трехмерным пространством Вселенной. Когда А много меньше 1, скорость роста Rглоб. во столько же раз больше скорости света и мы можем наблюдать лишь незначительную часть пространства Вселенной. Значения A меньше 1 соответствуют скорости роста Rглоб. больше скорости света. В случае, когда А равно 1 мы можем видеть объекты во Вселенной в пределах (четырехмерного — для трехмерной сферы) телесного угла по противоположным направления обзора равного двум радианам или примерно 120 градусов.
В-пятых, как известно существует «расстояние до поверхности последнего рассеяния». Это расстояние от Земли, до поверхности, за которой вся (в основном) первоначальная (образованная сразу после Большого взрыва) полностью ионизированная водородно-гелиевая плазма рекомбинировала с образованием нейтральных атомов и стала прозрачной для микроволнового излучения, образованного в результате рекомбинации атомов водорода (захвата протоном электрона на атомную орбиту). Так вот это расстояние, согласно последним данным наблюдений за указанным микроволновым излучением, называемым также «реликтовым излучением», либо «космическим микроволновым фоном», равно 3,1486 Хаббловских длин. Читателя с «незамыленным» взглядом сразу же должна насторожить «подозрительная» близость только что указанного числа 3,1486 к числу пи равному 3,1415. . А Хаббловская длина, как известно, равна расстоянию, которое свет в вакууме проходит за время возраста Вселенной равного 13,8 миллиардов световых лет. Как известно, «расстояние до поверхности последнего рассеяния» (от Земли) немного меньше «расстояния до горизонта частиц». «Расстояние до горизонта частиц» определяется в световых годах, как время за которое свет пройдет от Земли до максимально удаленных объектов во Вселенной при условии, что Вселенная при этом не будет расширяться. (Методы расчета этого расстояния вызывают у меня большие сомнения, но, тем не менее, я воспользуюсь известным общепризнанным мнением, что «расстояние до горизонта частиц» может быть равно «горизонту частиц», то есть расстоянию в реальном трехмерном пространстве Вселенной между максимально удаленными возможными объектами во Вселенной.) При этом следует различать понятия «горизонт частиц» и «расстояние до горизонта частиц» (расстояние от Земли), которое иногда путают даже серьезные астрономы. Если полагать, что глобальное пространство Вселенной евклидово («плоское»), то «расстояние до горизонта частиц» (расстояние от Земли) определяется расстоянием от Земли до центра шара, являющегося нашей Вселенной. Если полагать, что Земля находится в центре этого шара, то «расстояние до горизонта частиц» в два раза меньше «горизонта частиц»; а если полагать, что Земля находится на краю этого шара, то есть максимально удалена от его центра, то «расстояние до горизонта частиц» равно «горизонту частиц». Поскольку «расстояние до горизонта частиц» немного больше «расстояния до поверхности последнего рассеяния», то получается, что если Земля находится на краю вышеуказанного шара, являющегося нашей Вселенной», то «горизонт частиц» равен «расстоянию до горизонта частиц», и расстояние в реальном трехмерном пространстве Вселенной между максимально удаленными возможными объектами во Вселенной, равное диаметру вышеуказанного трехмерного шара, примерно равно 3,1486 Хаббловских длин (Хаббловская длина в световых годах — возраст Вселенной). (В световых годах это расстояние равно 3,1486 умножить на 13,8 миллиардов сетовых лет, то есть равно 43,45 миллиардов световых лет.) То есть, при предположения (условии), что пространство Вселенной евклидово («плоское») и, что Земля находится на краю вышеуказанного шара, то получается, что диаметр вышеуказанного трехмерного шара, являющегося нашей Вселенной, в световых годах в 3,1486 раз больше возраста Вселенной. В этом случае радиус Вселенной в световых годах в 1,5743 раз больше возраста Вселенной, что невозможно без вывода о том, что радиус Вселенной когда-то рос, со скоростью, превышающей скорость света в вакууме. Если же предположить, как считают некоторые авторы, что Земля и в такой «плоской» геометрии является не краем, а центром Вселенной, и что «горизонт частиц» в два раза дальше «расстояния (от Земли) до горизонта частиц», то ситуация для «плоской» (евклидовой) геометрии еще хуже, поскольку в этом случае мы должны считать, что «горизонт частиц» в два раза больше «расстояния до горизонта частиц», а радиус Вселенной в световых годах в 3,1486 раз больше возраста Вселенной.
Указанные противоречия и натяжки сразу же автоматически снимаются в предположении, что базовая геометрия глобального пространства Вселенной либо является геометрией трехмерной сферы, либо является геометрией обычного кубического трехмерного тора Клиффорда (T3-R6-0), свободно вписанного в шестимерное евклидово пространство и являющегося подмножеством пятимерной гиперсферы вложения, либо является геометрией сферического квази-кубического (R1(1)=R2(1)=R1(2) трехмерного тора Клиффорда (T3-R5-2), свободно вписанного в пятимерное евклидово пространство и являющегося подмножеством четырехмерной гиперсферы вложения. Сюда же мы можем добавить поверхности с незначительными или несущественными деформациями вышеуказанных поверхностей, а также различные квази-гиперсферические поверхности. Например, базовая (до квантового расслоения) геометрия глобального пространства Вселенной может являться геометрией самопересекающегося трехмерного гипертора (квази-гиперсферическая поверхность), для которого выполняются условия (R1 <<R3 и R2<<R3), где R1 — радиус его первой образующей окружности, R2 — радиус его второй образующей окружности, R3 — радиус его третьей образующей окружности. Здесь несмотря на выполнение условий R1<<R3 и R2<<R3, подразумевается, что гипертороидальное расслоение трехмерной сферы еще не является квантовым, обусловленным соотношением неопределенностей Гейзенберга, или иными сопоставимыми по порядку малости квантовыми эффектами.
Для указанных геометрий базового трехмерного пространства Вселенной «горизонт частиц» автоматически совпадает с «расстоянием до горизонта частиц» и равен длине максимальной полуокружности (половине меридиана) либо указанной трехмерной гиперсферы, либо трехмерной квази-гиперсферы, либо вышеуказанных гиперсфер вложения для соответствующих указанных торов Клиффорда. То есть «горизонт частиц» попросту равен числу пи (3,1415. ) умноженному на радиус либо соответствующей трехмерной гиперсферы, либо соответствующей трехмерной квази-гиперсферы, либо соответствующей гиперсферы вложения для соответствующих указанных торов Клиффорда. Дело здесь в том, что любая точка на поверхности гиперсферы, как и любая точка на поверхности обычной двумерной сферы не является ни ее центром, ни ее краем. В то же время, поскольку «расстояние до горизонта частиц» немного больше «расстояния до поверхности последнего рассеяния», то получается, что длина полуокружности указанных гиперсфер или квази-гиперсфер, равная «горизонту частиц», равна в световых годах Хаббловской длине (возрасту Вселенной) умноженной на 3,1486. Это означает, что радиус указанной трехмерной или соответствующей четырхмерной, или пятимерной гиперсферы или квази-гиперсферы, примерно равен Хаббловской длине, а точнее равен Хаббловской длине, умноженной на 1,00226=3,1486/3,1415 , то есть на отношение близкой к числу пи указанной величины равной 3,1486 к самому числу пи (3,1415. ). Поскольку методы определения указанной величины 3,1486 не дают надежды на ее достоверное определения с точностью до третьего знака после запятой, то мы можем с полным основанием и с хорошей точностью считать, что радиус указанной трехмерной или соответствующей четырехмерной, или пятимерной гиперсферы или квази-гиперсферы равен Хаббловской длине, то есть в световых годах равен возрасту Вселенной. В такой геометрии Вселенной «горизонт частиц» равен половине длины окружности с радиусом раным Хаббловской длине (возрасту Вселенной).
Таким образом, вышеуказанный экспериментально обнаруженный факт, что расстояние до поверхности последнего рассеяния равно 3,1486 (почти пи) Хаббловских длин, получает естественное «геометрическое» объяснение. Кроме того, такая геометрия означает, что радиус соответствующей трехмерной гиперсферы или соответствующей квази-гиперсферической трехмерной поверхности, являющейся базовым пространством нашей Вселенной, либо радиус соответствующей гиперсферы вложения для базового пространства Вселенной, моделируемого соответствующими указанными торами Клиффорда, совпадает с Хаббловской длиной, а также что этот радиус все время существования Вселенной рос со средней скоростью равной скорости света в вакууме. Поскольку у нас нет оснований полагать, что мы случайно проживаем именно в тот момент времени, когда средняя скорость роста этого радиуса совпала со скоростью света в вакууме, то это практически со сто процентной вероятностью означает, что указанный радиус всегда рос со скоростью равной скорости света в вакууме.
Таким образом, мы приходим к первому соотношению масштаба: радиус соответствующей трехмерной гиперсферы, либо четырехмерной или пятимерной гиперсфер вложения, либо соответствующей квази-гиперсферической трехмерной поверхности, с помощью которых мы моделируем базовое трехмерное пространство нашей Вселенной, совпадает с Хаббловской длиной, и растет практически равномерно во времени со скоростью равной скорости света в вакууме, которая является практически постоянной за все время существования Вселенной.
Для нас это фактически эквивалентно закону сохранения кинетической энергии расширения базового трехмерного пространства Вселенной:
E=M*C*С, где: E — совокупная кинетическая энергия трехмерной поверхности, являющейся базовым трехмерным пространством Вселенной; M — совокупная эффективная масса (вероятно гравитационная масса) трехмерной поверхности, являющейся базовым трехмерным пространством Вселенной; С — скорость увеличения радиуса соответствующей гиперсферы (соответствующей трехмерной гиперсферы, либо соответствующей трехмерной квази-гиперсферы, либо соответствующей гиперсферы вложения для соответствующих указанных торов Клиффорда, с помощью которых мы моделируем базовое трехмерное пространство Вселенной), совпадающая со скоростью света в вакууме.
То есть, радиус указанных трехмерной гиперсферы, в том числе трехмерной гиперсферы, которой мы аппроксимируем в соответствующей глобальной части наш трехмерный тор (гипертор), либо радиус соответствующей пятимерной или шестимерной гиперсфер вложения для указанных соответствующих торов Клиффорда, должен расти со временем согласно формуле:
где: Tглоб. — глобальное время Вселенной,
C — скорость света в вакууме,
Rглоб. — радиус глобального базового пространства Вселенной, понимаемый как радиус соответствующей нашей трехмерной (или пятимерной или шестимерной для соответствующих торов Клиффорда) гиперсферы или квази-гиперсферы (глобального пространства Вселенной).
То есть ранее указанный соответствующий постоянный численный коэффициент A равен единице.
При такой геометрии в электромагнитных волнах (фотонах) мы можем наблюдать только одно полушарие, (а точнее гипер-сферический угол равный 2 радиана, то есть примерно 120 градусов, что меньше полушария с углом равным 180 градусов), соответствующей гиперсферической или квази-гипресферической поверхности. Следует при этом заметить, что этот максимально наблюдаемый угол касается и самой поверхности последнего рассеяния. Иной — больший или меньший угол поверхности последнего рассеяния мы могли бы наблюдать, если бы некоторое время после последнего рассеяния радиус соответствующей гиперсферы или квази-гиперсферы (глобального пространства Вселенной) рос бы со скоростью соответственно меньшей или большей скорости света.
При этом мы, находясь в геометрическом центре такого полушария, всегда будем наблюдать, что одни и те же максимально удаленные видимые нами галактики и звезды будут всегда удаляться от нас со скоростями почти равными скорости света и не будут исчезать из вида, но при этом на горизонте Вселенной не будут появляться новые галактики и звезды, которых ранее было невозможно увидеть, а видимая часть поверхности последнего рассеяния не будет уменьшаться или увеличиваться и не будет видоизменяться, что собственно пока и наблюдается. То есть мы всегда будем наблюдать, что максимально удаленные видимые нами галактики удаляются от нас со скоростью близкой к скорости света в вакууме и находятся от нас на расстоянии немного меньшем хаббловской длины, что собственно и наблюдается.
Все другие виды геометрии базового трехмерного глобального пространства Вселенной я полагаю невозможными, поскольку для соответствия указанным фактам они требуют слишком большого количества искусственных допущений. Например, «плоская» (евклидова, то есть не криволинейная) модель Лямбда-CDM космологической теории, уже потребовала предположения о довольно сложной, а потому крайне маловероятной динамике расширения Вселенной, а именно о первоначальной космической инфляции глобального пространства (расширение всего пространства со скоростями превышающими скорость света в вакууме), а также о смене замедленного расширения на ускоренное расширение. Полагаю, что недостаточность наблюдаемого красного смещения для объяснения малой светимости соответствующих стандартных свечей имеет куда более прозаическое объяснение, чем увеличение плотности неизвестно откуда берущейся темной энергии. Например, в ранней Вселенной химический состав ядра стандартной свечи мог существенно отличаться от его состава в зрелой и поздней Вселенной, что и приводило к более слабому взрыву, то есть к отклонению от современного стандарта. Не исключено, что и существенно большая кривизна глобального пространства в ранней Вселенной так же могла приводить к более раннему и слабому взрыву, то есть к отклонению стандартной свечи от современного стандарта. Неплохо бы просчитать и уменьшение светимости при переходе от евклидовой (плоской) к римановой (сферической) топологии.
Итак, мы доказали на основе наблюдаемых данных, что первым таким соотношением масштаба является следующее: радиус соответствующей трехмерной гиперсферы, либо четырехмерной или пятимерной гиперсфер вложения для соответствующих торов Клиффорда, либо соответствующей квази-гиперсферической трехмерной поверхности, с помощью которых мы моделируем базовое трехмерное пространство нашей Вселенной, совпадает с Хаббловской длиной, и растет практически равномерно во времени со скоростью равной скорости света в вакууме, которая является практически постоянной за все время существования Вселенной.
Мы записали первое (глобальное) соотношение масштаба в виде следующей формулы:
Rглоб.=С*Tглоб. (2)
где: Rглоб. — радиус глобального базового пространства Вселенной, понимаемый как радиус соответствующей трехмерной сферы (гиперсферы), либо четырехмерной или пятимерной сфер (гиперсфер) вложения для соответствующих торов Клиффорда, либо соответствующей квази-гиперсферической трехмерной поверхности, с помощью которых мы моделируем базовое трехмерное пространство нашей Вселенной;
Tглоб. — глобальное (базовое (не квантовое)) время Вселенной;
С — скорость света в вакууме.
В общефилософском смысле и в соответствии с излагаемой нами концепцией, значение скорости света в вакууме является следствием и определяется именно указанной постоянной скоростью увеличения радиуса соответствующей трехмерной гиперсферы, либо четырехмерной или пятимерной гиперсфер вложения для соответствующих торов Клиффорда, либо соответствующей квази-гиперсферической трехмерной поверхности, с помощью которых мы моделируем глобальное базовое трехмерное пространство нашей Вселенной.
Для нас это фактически эквивалентно закону сохранения «приведенной кинетической» энергии, а также собственной энергии расширения базового трехмерного пространства Вселенной:
где: Eглоб.пр. — собственная кинетическая энергия расширения трехмерной поверхности, являющейся базовым трехмерным пространством Вселенной;
Mглоб.пр. — совокупная эффективная масса (вероятно совпадающая с гравитационной массой) трехмерной поверхности, являющейся базовым трехмерным пространством Вселенной;
С — скорость увеличения радиуса соответствующей гиперсферы (соответствующей трехмерной гиперсферы, либо соответствующей трехмерной квази-гиперсферы, либо соответствующей гиперсферы вложения для соответствующих нижеуказанных торов Клиффорда, с помощью которых мы моделируем базовое трехмерное пространство Вселенной), совпадающая со скоростью света в вакууме.
В такую «приведенную кинетическую» или полную энергию расширения базового трехмерного пространства Вселенной, могут входить, как собственная кинетическая, так и потенциальная энергия расширения пространства Вселенной, обусловленная наличием у него глобальной положительной кривизны, стремящейся увеличивать радиус пространства, и гравитационного само-притяжения, стремящегося схлопнуть пространство в точку. В гиперсферической или квази-гиперсферической геометрии обе силы, по крайней мере при указанной постоянной скорости расширения, должны уравновешивать друг друга. Действительно, положительная компонента потенциальной энергии, обусловленная наличием глобальной кривизны пространства Вселенной прямо пропорциональна полной скалярной кривизне пространства, то есть обратно пропорциональна квадрату его глобального радиуса — радиуса соответствующей гиперсферы (или квази-гиперсферы). В то же время, действующей гравитационной силой самосжатия глобального пространства Вселенной является лишь компонент гравитационной силы, направленный к геометрическому центру трехмерной (или четырехмерной или пятимерной для соответствующих торов Клиффорда) гиперсферы, вследствие уравновешивающего эффекта сил, действующих по касательной к поверхности гиперсферы. Поэтому, для того чтобы получить соответствующий отрицательный потенциал и отрицательную энергию этой действующей гравитационной силы самосжатия глобального пространства Вселенной (указанного компонента гравитационной силы, направленный к геометрическому центру), необходимо обычный отрицательный гравитационный потенциал обратно пропорциональный расстоянию, в данном случае обратно пропорциональный радиусу соответствующей гиперсферы, еще раз разделить на радиус этой гиперсферы. То есть отрицательная компонента потенциальной энергии, обусловленная гравитационным само-сжатием пространства Вселенной, также обратно пропорциональна квадрату его глобального радиуса — радиуса соответствующей гиперсферы (или кваз-гиперсферы). Поскольку оба указанных компонента полной собственной потенциальной энергии пространства Вселенной имеют изначально гравитационную природу, мы с неизбежность приходим к гипотезе о том, что указанные силы расширения и сжатия пространства Вселенной должны уравновешивать друг друга. А подтверждением этой гипотезы является вышеуказанный астрономически наблюдаемый факт увеличения радиуса пространства Вселенной — радиуса соответствующей трехмерной (или четырехмерной или пятимерной для соответствующих торов Клиффорда) гиперсферы со скоростью равной скорости света в вакууме. В классическом идеале полная потенциальная энергия пространства Вселенной равна нулю, или, что по смыслу — тоже самое, константе, и мы приходим к тому, что «приведенная кинетическая» энергия расширения пространства превращается в простую кинетическую энергию его расширения, которая является константой. Что является дополнительным, хотя и косвенным, подтверждением наличия у пространства Вселенной не только собственной кинетической энергии, но и собственной гравитационной, и собственной инерционной массы.
К сожалению, в результате печально сложившегося консенсуса в настоящее время доминирует Лямбда-CDM (темная энергия (лямбда-член)- темная материя (CDM)) космологическая теория, постулирующая плоское пространство Вселенной, искусственно привлекающая необъясняемые и ненаблюдаемые темную энергию и темную материю, для объяснения движений звезд и галактик, которые не могут быть объяснены в «плоском пространстве» гравитацией наблюдаемой материи (вещества звезд, газа и черных дыр). И уж если называть вещи своими именами, то Лямбда-CDM космологическая теория это пример, свойственного всей истории человечества и истории науки в частности, коллективного и не вполне бескорыстного заблуждения. Наиболее «серьезным» аргументом в пользу «плоского пространства» является «наблюдаемый» якобы факт, говорящий о том, что сумма углов «глобального Вселенского треугольника», построенного с помощью наблюдения с Земли пятна флуктуации реликтового излучения, с точность до 0,1 процента равна 180 градусов. Но если расстояние (в световых годах) до этого пятна, а точнее расстояние до поверхности последнего рассеяния еще можно с некоторыми натяжками считать оцененным правильно, а угловой размер этого пятна можно считать измеренным верно, то оценка размеров этого пятна в световых годах не выдерживает уже никакой критики и кишит теми же тавтологическими приемами и теми же недоказанными допущениями, что и введение темной материи и темной энергии. По существу метод оценки размеров пятна флуктуации реликтового излучения в световых годах уже опирается на постулат о том, что глобальное пространство Вселенной является евклидовым по крайней мере на размерах наблюдаемой Вселенной. А потому ни о какой якобы «измеренной» и составляющей 180 градусов сумме углов «глобального Вселенского треугольника» не может быть и речи.
Кроме того, существует закрытое трехмерное риманово пространство, обладающее глобальной кривизной, но сохраняющее, так же как и поверхность двумерного цилиндра, сумму углов треугольника равной 180 градусов. Это пространство (трехмерная поверхность) обычного трехмерного тора Клиффорда (T3-R6-0) (S1*S1*S1) — трехмерного тора свободно вписанного в шестимерное евклидово пространство. В аналитической геометрии и топологии обычный трехмерный тор Клиффорда (T3-R6-0) часто называют также кубическим тором. (К сожалению в космической топологии кубическим тором часто ошибочно называют обычный трехмерный гипертор (трехмерный тор T3-R4) свободно вписанный в четырехмерное евклидово пространство, когда рассматривают его в качестве фундаментальной кубической (в общем случае параллелепипедной) ячейки универсального накрывающего пространства в виде разбитого на такие же ячейки евклидова трехмерного пространства. Эта ошибка и вытекающая из нее путаница не редко приводит авторов к ошибочным расчетам или оценкам.) Кроме того существуют два вида частично закрытого трехмерного риманова пространства также сохраняющие сумму углов треугольника равной 180 градусов. Это пространство (трехмерная поверхность) простого (одинарного) трехмерного цилиндра Клиффорда (S1*R1*R1) в другой записи (S1*R2), а также пространство (трехмерная поверхность) тороидального (двойного) трехмерного цилиндра Клиффорда (S1*S1*R1).
В конце концов нашу Вселенную можно гипотетически представить в виде не только бесконечно малой части бесконечного открытого евклидова пространства, но и в виде достаточно малой части огромного риманова пространства (например трехмерной гиперсферы или трехмерного гипертора); в этих (последних) случаях, даже если сумма углов «глобального Вселенского треугольника» и иных наблюдаемых во Вселенной (Вселенной Большого взрыва) больших треугольников действительно окажется очень близка к 180 градусам, этот факт легко будет объяснить достаточной малостью радиуса наблюдаемой Вселенной (материи образовавшейся в результате Большого взрыва), по сравнением с размерами и радиусом (радиусами) глобального риманова пространства, (в котором наблюдаемая Вселенная (Вселенная Большого взрыва) занимает лишь небольшую часть).
И, наконец, в трехмерном пространстве Вселенной, являющемся трехмерной гиперсферой (или квази-гиперсферой, или принадлежащем соответствующей четырехмерной или пятимерной гиперсфере для глобального пространства в виде соответствующих торов Клиффорда), радиус которой растет со скорость света в вакууме, у любого луча света, кроме составляющей скорости, которая геометрически является касательной к базовому глобальному трехмерному пространству, являющемуся трехмерной сферой (или соответствующим трехмерным тором Клиффорда, или соответствующей трехмерной квази-гиперсферой), имеется еще и радиальная составляющая скорости, перпендикулярная базовому глобальному трехмерному пространству Вселенной, которая возникает вследствие роста указанного радиуса (трехмерной гиперсферы или квази-гиперсферы, или соответствующей четырехмерной или пятимерной гиперсферы для глобального пространства в виде соответствующих торов Клиффорда). В силу наличия этой указанной составляющей скорости, которая перпендикулярна базовому глобальному трехмерному пространству Вселенной и также равна скорости света в вакууме, реальная траектория свободно (без влияния вложенной барионной (и иной возможной вложенной) материи и черных дыр) распространяющегося света всегда будет четырехмерной, то есть не будет иметь той же самой глобальной кривизны, которая свойственна самому риманову базовому глобальному трехмерному пространству Вселенной. Здесь скажутся: эффект изменения собственной глобальной кривизны пространства с течением времени распространения света; эффект наличия радиальной составляющей скорости распространения света, обусловленный ростом радиуса трехмерной гиперсферы; и вероятно специфика релятивистского сложения скоростей. Эти эффекты также необходимо учитывать при измерении кривизны базового глобального трехмерного пространства Вселенной методами непосредственного визуального измерения.
В сулу указанных обстоятельств свет от вышеуказанного пятна реликтового излучения распространяется практически прямолинейно в соответствующем четырехмерном пространстве вложения нашей трехмерной сферы, моделирующей глобальное базовое пространства Вселенной, (или в соответствующих пятимерном или шестимерном пространствах вложения для соответствующих четырехмерной или пятимерной сферы для глобального пространства в виде соответствующих торов Клиффорда). Действительно, угловое расстояние от Земли или соответствующей ей собственной точки глобального базового пространства Вселенной до любой видимой точки поверхности последнего рассеяния одинаково и зависит от соотношения средней эффективной скорости увеличения радиуса нашей трехмерной сферы и скорости света в вакууме. Если считать, что скорость увеличения радиуса нашей трехмерной сферы равна скорости света в вакууме, то это угловое расстояние равно одному радиану. Это угловое расстояние рассчитывается, как угол между двумя лучами исходящими из центра нашей трехмерной сферы и проходящими один в направлении на Землю, другой в направлении на соответствующую точку поверхности последнего рассеяния. При этом фактическое эффективное расстояние от Земли до любой точки поверхности последнего рассеяния не может превышать диаметра (размера) всей поверхности последнего рассеяния, которая равна всего-то 380000 световых лет умножить на 2, поскольку соответствующее угловое расстояние не увеличивается, а свет, достигающий от этой точки до Земли (изначально также находящейся внутри области последнего рассеяния) двигается по кратчайшей в трехмерном пространстве траектории и не поворачивает вспять. Таким образом радиальный (в направлении от центра нашей трехмерной сферы) путь света от любой выбранной нами точки поверхности последнего рассеяния до Земли равен в световых годах возрасту Вселенной (или Хаббловской длине), то есть составляет примерно 13,8 миллиардов световых лет, в то время, как путь света вдоль поверхности нашей трехмерной сферы (путь ортогональный радиальному) не может превышать в световых годах 0,76 миллионов световых лет. Таким образом путь света от выбранной нами точки поверхности последнего рассеяния до Земли вдоль поверхности нашей трехмерной сферы (путь ортогональный радиальному) примерно в 20000 раз меньше пути этого же света в радиальном направлении. Следовательно, для обнаружения эффектов кривизны нашей трехмерной сферы, методами измерения с Земли суммы углов глобальных Вселенских треугольников, одна из сторон которых является пятном реликтового излучения, необходима точность не менее 0,005%. Заявленная же точность вышеуказанного эксперимента равна 0,1%. Следовательно, вышеуказанное широко разрекламированное экспериментальное доказательство евклидовости (плоскостности) пространства Вселенной, является не более чем очередной научной фикцией, коими столь изобилует современная наука и, к сожалению, в особенности физика. При этом я ничуть не умаляю и значимости и многочисленности ее современных достижений и побед.
Видео:Урок 114. Работа. Теорема о кинетической энергииСкачать

Кинетическая энергия по окружности
Видео:Урок 86 (осн). Энергия. Превращения энергииСкачать

Кинетическая энергия по окружности
«Физика — 10 класс»
Почему для увеличения угловой скорости вращения фигурист вытягивается вдоль оси вращения.
Должен ли вращаться вертолёт при вращении его винта?
Заданные вопросы наводят на мысль о том, что если на тело не действуют внешние силы или действие их скомпенсировано и одна часть тела начинает вращение в одну сторону, то другая часть должна вращаться в другую сторону, подобно тому как при выбросе горючего из ракеты сама ракета движется в противоположную сторону.
Момент импульса.
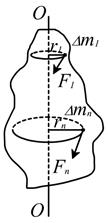
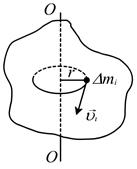
Если рассмотреть вращающийся диск, то становится очевидным, что суммарный импульс диска равен нулю, так как любой частице тела соответствует частица, движущаяся с равной по модулю скоростью, но в противоположном направлении (рис. 6.9).
Но диск движется, угловая скорость вращения всех частиц одинакова. Однако ясно, что чем дальше находится частица от оси вращения, тем больше её импульс. Следовательно, для вращательного движения надо ввести ещё одну характеристику, подобную импульсу, — момент импульса.
Моментом импульса частицы, движущейся по окружности, называют произведение импульса частицы на расстояние от неё до оси вращения (рис. 6.10):
Линейная и угловая скорости связаны соотношением v = ωr, тогда
Все точки твёрдого дела движутся относительно неподвижной оси вращения с одинаковой угловой скоростью. Твёрдое тело можно представить как совокупность материальных точек.
Момент импульса твёрдого тела равен произведению момента инерции на угловую скорость вращения:
Момент импульса — векторная величина, согласно формуле (6.3) момент импульса направлен так же, как и угловая скорость.
Основное уравнение динамики вращательного движения в импульсной форме.
Угловое ускорение тела равно изменению угловой скорости, делённому на промежуток времени, в течение которого это изменение произошло: 

Изменение момента импульса равно произведению суммарного момента сил, действующих на тело или систему, на время действия этих сил.
Закон сохранения момента импульса:
Если суммарный момент сил, действующих на тело или систему тел, имеющих неподвижную ось вращения, равен нулю, то изменение момента импульса также равно нулю, т. е. момент импульса системы остаётся постоянным.
Изменение импульса системы равно суммарному импульсу сил, действующих на систему.
Вращающийся фигурист разводит в стороны руки, тем самым увеличивает момент инерции, чтобы уменьшить угловую скорость вращения.
Закон сохранения момента импульса можно продемонстрировать с помощью следующего опыта, называемого «опыт со скамьёй Жуковского». На скамью, имеющую вертикальную ось вращения, проходящую через её центр, встаёт человек. Человек держит в руках гантели. Если скамью заставить вращаться, то человек может изменять скорость вращения, прижимая гантели к груди или опуская руки, а затем разводя их. Разводя руки, он увеличивает момент инерции, и угловая скорость вращения уменьшается (рис. 6.11, а), опуская руки, он уменьшает момент инерции, и угловая скорость вращения скамьи увеличивается (рис. 6.11, б).
Человек может также заставить вращаться скамью, если пойдёт вдоль её края. При этом скамья будет вращаться в противоположном направлении, так как суммарный момент импульса должен остаться равным нулю.
На законе сохранения момента импульса основан принцип действия приборов, называемых гироскопами. Основное свойство гироскопа — это сохранение направления оси вращения, если на эту ось не действуют внешние силы. В XIX в. гироскопы использовались мореплавателями для ориентации в море.
Кинетическая энергия вращающегося твёрдого тела.
Кинетическая энергия вращающегося твёрдого тела равна сумме кинетических энергий отдельных его частиц. Разделим тело на малые элементы, каждый из которых можно считать материальной точкой. Тогда кинетическая энергия тела равна сумме кинетических энергий материальных точек, из которых оно состоит:
Угловая скорость вращения всех точек тела одинакова, следовательно,
Величина в скобках, как мы уже знаем, это момент инерции твёрдого тела. Окончательно формула для кинетической энергии твёрдого тела, имеющего неподвижную ось вращения, имеет вид
В общем случае движения твёрдого тела, когда ось вращения свободна, его кинетическая энергия равна сумме энергий поступательного и вращательного движений. Так, кинетическая энергия колеса, масса которого сосредоточена в ободе, катящегося по дороге с постоянной скоростью, равна
В таблице сопоставлены формулы механики поступательного движения материальной точки с аналогичными формулами вращательного движения твёрдого тела.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
Видео:Потенциальная и кинетическая энергияСкачать

Закон сохранения энергии для вращательного движения
1. Момент импульса, законы изменения и сохранения момента импульса.
2. Работа и кинетическая энергия при вращательном движении. Закон изменения и сохранения механической энергии при вращательном движении.
3. Сопоставление поступательного и вращательного движений. Заключение.
ОТВОДИМОЕ ВРЕМЯ: 2 часа.
1. Суханов курс физики. – М.: 1996.
2. Савельев общей физики. Том 1. – M: – Наука, 1996. § 29, 41,42,43.
3. Трофимова физики. – М.: Высшая школа, 1999. § 17,19.
4. , Детлаф по физике. – М.: Наука, 1996. Глава 5.
Материальное обеспечение занятия:
Демонстрации: «Скамья Жуковского», «Фигурист».
Наряду с законами сохранения энергии и импульса закон сохранения момента импульса является одним из важнейших Фундаментальных законов природы.
В физике понятие, момента импульса расширяют на немеханические системы (которые не подчиняются законам Ньютона) и постулируют закон сохранения импульса для всех физических процессов.
I. МОМЕНТ ИМПУЛЬСА. ЗАКОН ИЗМЕНЕНИЯ И ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Вспомним основной закон динамики вращательного движения:

учтем, что 

Поскольку предполагалось, что момент инерции J=const можно внести его под знак дифференциала.
Тогда получим 


Скорость изменения момента импульса тела равна векторной сумме моментов сил, действующих на тело.
Это более общая формулировка основного закона вращательного движения, она справедлива и для тела с изменяющимся моментом инерции.
Момент импульса измеряется в 1кг·м/с. Килограмм-метр в квадрате в секунду равен моменту импульса тела с моментом инерции 1кг·м, вращающегося с угловой скоростью 1рад/с.
Момент импульса – вектор, его направление всегда совпадает с направлением угловой скорости (рис 1).
Выберем произвольную систему тел.
Ведем понятие момента импульса данной системы как векторную сумму моментов импульсов ее отдельных частей:

где все векторы определены относительно одной и той же оси вращения заданной системы отсчета. Момент импульса системы тел – величина аддитивная; момент импульса системы тел равен векторной сумме моментов импульсов ее отдельных частей независимо от того, взаимодействуют они между собой или нет.
Выясним, какая величина определяет изменение момента импульса системы тел. Продифференцируем (3) по-времени:

Из Формулы (2) ясно, что 

где 

Суммарный момент всех внутренних сил относительно любой точки равен нулю, так как внутренние силы – это взаимодействия между частицами системы. По третьему закону Ньютона эти силы попарно равны по модулю, противоположны по направлению и лежат на одной прямой, то есть имеют одинаковые радиус-векторы. Поэтому моменты сил каждой пары взаимодействия равны по модулю и противоположны по направлению, Значит, суммарный момент всех внутренних сил равен нулю.

В результате уравнение (5) принимает вид:

где 
Производная момента импульса системы по времени равна суммарному моменту всех внешних сил относительна данной оси.
Пришли к важному выводу в уравнении (7): момент импульса системы тел может изменяться под действием только суммарного момента всех внешних сил.
В проекциях на оси неподвижной прямоугольной декартовой системе координат с началом в точке 0 закон изменения момента импульса системы записывается в виде:

Здесь Lx, Ly, Lx и Mx, My, Mx – моменты импульса системы и главные моменты внешних сил относительно соответствующих осей координат.
Из основного закона динамики вращательного движения следует закон сохранения момента импульса.
Момент импульса замкнутой системы относительно любой неподвижной точки не изменяется с течением времени.
Для замкнутой системы 


Закон сохранения момента импульса принадлежит к числу самых фундаментальных физических законов, он связан с изотропностью пространства. Изотропность пространства проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора направления осей координат инерциальной системы отсчета, т. е. не изменяются при повороте в пространстве замкнутой системы как целого на любой угол.
Особый интерес представляет случай, когда момент импульса сохраняется для незамкнутой системы. Если относительно некоторой оси выбранной системы отсчета главный момент внешних сил 
Обычно 



Система тел: скамья, человек, гантели,
Эта система не замкнутая, но момент внешних сил относительно вертикальной оси Z равен нул^, следовательно

Подставляем
Найдем 
где J0 – момент инерции скамьи с человеком, m – масса одной гантели, r1 – расстояние гантели до оси в первом случае, r2 – расстояние гантели до оси во втором случае.

Пусть твердое тело движется поступательно под действием консервативных и неконсервативных сил, т.е. общий случай. Тогда равнодействующая всех сил, действующих на тело 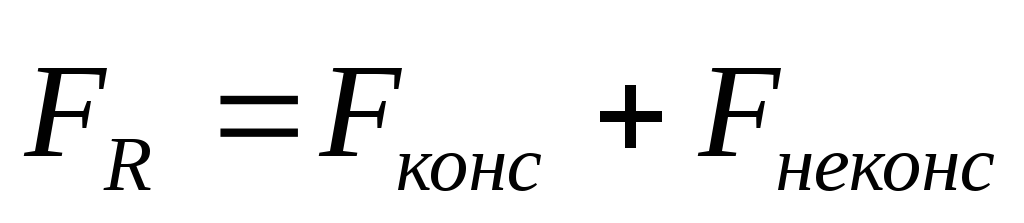

По теореме о кинетической энергии 

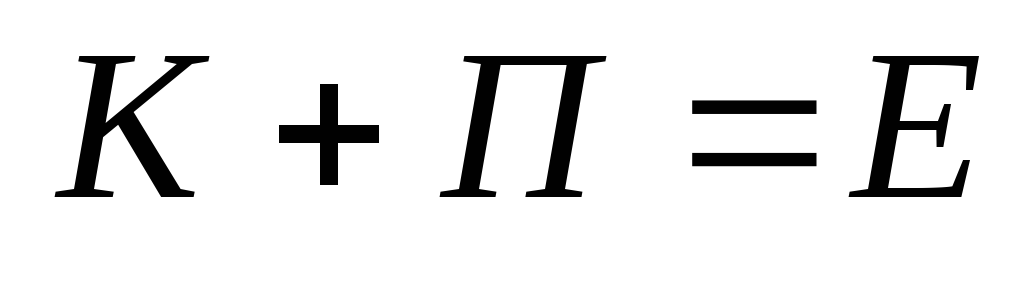

Если 

Формулировка закона сохранения энергии:
Полная механическая энергия тела не изменяется в отсутствии работы неконсервативных сил.
Для механической системы из Nчастиц нетрудно показать, что (*) имеет место.

Первая сумма здесь – суммарная кинетическая энергия системы частиц.
Вторая – суммарная потенциальная энергия частиц во внешнем поле консервативных сил
Третья – потенциальная энергия взаимодействия частиц системы друг с другом.
Вторая и третья суммы представляют собой полную потенциальную энергию системы.

Работа неконсервативных сил состоит из двух слагаемых, представляемых собой работу внутренних и внешних неконсервативных сил 
Также как и в случае движения отдельного тела, для механической системы из Nтел, если

Полная механическая энергия системы частиц, находящихся только под действием консервативных сил, сохраняется.
Таким образом, при наличии неконсервативных сил полная механическая энергия не сохраняется.
Неконсервативными силами являются, например, сила трения 

Силы, приводящие к дессинации называются дессинативными. Некоторые силы не обязательно являются дессинативными.
Закон сохранения энергии имеет всеобщий характер и применим не только к механическим явлениям, но и ко всем процессам в природе. Полное количество энергии в изолированной системе тел и полей всегда остается постоянным. Энергия лишь может переходить из одной формы в другую.
Динамика вращательного движения
Видео:Потенциальная и Кинетическая🤔Скачать

§12. Кинетическая энергия вращательного движения твердого тела. Момент инерции тел
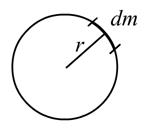
Рассмотрим твердое тело, вращающееся на неподвижной оси.
Мысленно разобьем его на Nэлементарных участков с массой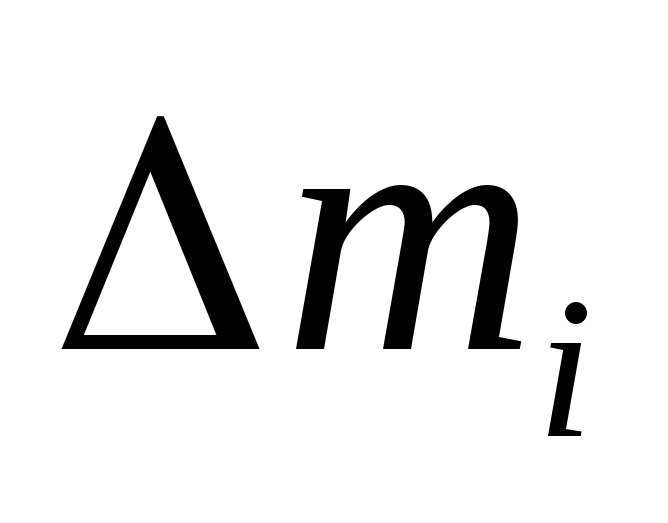

(т.к. кинетическая энергия – величина аддитивная).
Ясно, что все элементарные участки вращаются по окружности, разного радиуса, но с одинаковой угловой скоростью 

Если размеры тела много меньше расстояния от него до некоторой его оси вращения z, то произведение массы этого тела на квадрат расстояния до данной оси вращения называется моментом инерции этого тела относительно оси вращенияz:
В нашем случае 
Моментом инерции всего тела вращения называется сумма моментов инерции всех его элементарных частей
Суммирование по элементарным участкам определяется разбиением, и лишь при 

Таким образом, кинетическая энергия есть
поступательное движение вращательное движение




при движении при вращении
Моменты инерции некоторых однородных (
Момент инерции обруча или тонкостенного цилиндра относительно оси, проходящей через центр инертности перпендикулярно плоскости обруча.
Момент инерции диска или цилиндра относительно оси симметрии тела.
Выберем внутри цилиндра тонкостенный цилиндр с 

Учитывая, что 

Момент инерции плоского стержня относительно оси, проходящей через центр тела и перпендикулярно к нему
Момент инерции шара относительно оси, проходящей через его центр.
1. Момент импульса вpащающегося, тела относительно оси
L = Jw.
2. Закон сохpанения момента импульса
SL = const.
где L – момент импульса i-го тела, входящего в состав системы. Закон сохpанения момента импульса для двух взаимодействующих тел
где J1, J2, w1, w2 – моменты инеpции и угловые скоpости
тел до взаимодействия, J1 / , J2 / , w1 / , w2 / – те же величины после
взаимодействия. Закон сохpанения момента импульса для одного тела, момент инеpции, котоpого меняется,
где J1 и J2 – начальный и конечный моменты инеpции, w1 и w2 –
начальная и конечная угловые скоpости тела.
3. Между формулами, описывающими поступательное и вращательное движения есть аналогия:
Wk = ( mv 2 )/2; Wk = (Jw 2 )/2;
С. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ.
1. Уравнение гармонических колебаний
x = Acos(wt + j),
где х– смещение точки от положения равновесия;t – время;
А, w, j – соответственно амплитуда, угловая частота, начальная фаза колебаний; (wt + j)-фаза колебания в моментt
2. Угловая частота колебаний w = 2pn, или w = 2p/T,
где n и T – частота и период колебаний.
3. Скорость точки, совершающей гармонические колебания,
v = x / = – Awsin(wt + j).
4. Ускорение при гармоническом колебании
a = x // = – Aw 2 cos(wt + j).
5. Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящими по одной прямой, определяется по формуле
где А1 и А2 – амплитуды составляющих колебаний; j1 и j2 – их начальные фазы.
6. Дифференциальное уравнение гармонических колебаний материальной точки mx // = – kx, или x // + wx = 0,
гдеm – масса точки; k -коэффициент квазиупругой силы (kw 2 ) . 7. Полная энергия материальной точки, совершающей гармонические колебания, W = (mA 2 w 2 )/2 = (kA 2 )/2.
8. Период колебаний тела, подвешенного на пружине
T = 2pÖ(m/k),
где m – масса тела; k– жесткость пружины.
9. Период колебаний математического маятника T = 2pÖ(l/g),
гдеl – длина маятника; g – ускорение свободного падения.
10. Период колебаний физического маятника T = 2pÖ(J/mgl).
11. Период крутильных колебаний тела, подвешенного на упругой нити T = 2pÖ(J/k),
где J– момент инерции тела относительно оси, совпадающей с упругой нитью; k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
12. Дифференциальное уравнение затухающих колебаний
mx // = – kx – rx / , или x // +2dx / + w 2 x = 0,
где r – коэффициент сопротивления; d – коэффициент затухания; d = r/(2m); w – cобственная частота колебаний (w = Ö(k/m).
13. Уравнение затухающих колебаний x = A . e – d t .cos(wt + j)
где А – начальная аплитуда; w – частота; е – основание натурального логарифма; d – коэффициент затухания.
14. Дифференциальное уравнение вынужденных колебаний
mx // = – kx – rx / + F .cos(wt), или x // + 2dx / + w 2 x = f .cos(wt).
где F .cos(wt) – внешняя периодическая сила, действующая на колеблющуюся точку и вызывающая вынужденные колебания; F – ее амплитудное значение; f = F /m.
Вариант 1.
Кинематика.
А.1. Пуля пущена с начальной скоростью vпод углом aк горизонту. Определить максимальную высоту подъема, дальность полета и радиус кривизны траектории пули в ее наивысшей точке.
Динамика.
Б.1.Через блок массой Мперекинута невесомая, нерастяжимая нить, к концам которой подвешены грузы с массами m1и m2 . Определить ускорения, с которыми будут двигаться грузы, если их предоставить самим себе, трением в оси блока пренебречь.
Законы сохранения при прямолинейном движении.
В.1.Тело массой m1движется навстречу второму телу массой m2 и абсолютно не упруго соударяется с ним. Скорости тел непосредственно перед ударом были v1 и v2 . Определить расстояние, пройденное телами после удара, если коэффициент трения μ ?
Энергия и работа.
Д.1. Под действием постоянной силы F вагонетка прошла путь Sи приобрела скорость v . Определить работу силы, если масса вагонетки равна m и коэффициент трения k .
Законы сохранения при вращательном движении.
Е.1. Стержень длиной Lи массой M может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. В середину стержня ударяет пуля массой m2,летящая в горизонтальном направлении со скоростью vи застревает в нем. На какой угол отклонится стержень после удара?
6. Механические колебания.
С.1.Частица массой m совершает гармонические колебания с циклической частотой ω , по закону x= Asin(ωt). Определить период колебаний и амплитуду колебаний, если максимальная сила, действующая на частицу, равна F . Определить, также кинетическую, потенциальную и полную энергии через время tот начала колебания.
Вариант 2.
Кинематика.
А.2. Точка движется по окружности так, что зависимость пути от времени дается уравнением S = А – Bt + Ct 2 . Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорения.
Динамика.
Б.2.Акробат на мотоцикле описывает «мертвую петлю» радиусом R. С какой наименьшей скоростью должен проезжать акробат верхнюю точку петли, чтобы не сорваться?
Видео:Физика - движение по окружностиСкачать

Кинетическая энергия вращения
Лекция 3. Динамика твердого тела
План лекции
3.2. Основные уравнения вращательного движения. Момент инерции.
3.3. Кинетическая энергия вращения.
3.4. Момент импульса. Закон сохранения момента импульса.
3.5. Аналогия между поступательным и вращательным движением.
Момент силы
Рассмотрим движение твердого тела вокруг неподвижной оси. Пусть твердое тело имеет неподвижную ось вращения ОО (рис.3.1) и к нему приложена произвольная сила 
Рис. 3.1
Разложим силу 
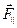
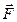
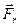
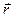
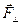
Не любая сила, приложенная к телу, будет вращать его. Силы 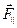
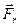
Сила 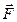
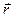
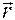
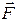
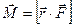
Вектор 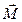
Модуль момента силы
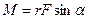
где α – угол между векторами 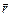
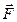
Из рис.3.1. видно, что 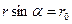
r0 – кратчайшее расстояние от оси вращения до линии действия силы и называется плечом силы. Тогда момент силы можно записать
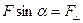
где F 
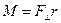
Если на тело действует несколько сил, то результирующий момент силы равен векторной сумме моментов отдельных сил, но так как все моменты направлены вдоль оси, то их можно заменить алгебраической суммой. Момент будет считаться положительным, если он вращает тело по часовой стрелке и отрицательным, если против часовой стрелки. При равенстве нулю всех моментов сил ( 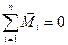
Понятие момента силы можно продемонстрировать с помощью «капризной катушки». Катушку с нитками тянут за свободный конец нитки (рис. 3.2).
Рис. 3.2
В зависимости от направления силы натяжения нити 
Используя условие равновесия ( 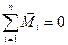
3.2. Основное уравнение вращательного
движения. Момент инерции
Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси ОО (рис.3.3). Разобьём мысленно это тело на элементы массами Δm1, Δm2, …, Δmn. При вращении эти элементы опишут окружности радиусами r1, r2, …, rn . На каждый элемент действуют соответственно силы F1, F2, …, Fn . Вращение тела вокруг оси ОО происходит под действием полного момента сил М.
Согласно II закону Ньютона, каждая сила F, действующая на элемент массой Dm, вызывает ускорение данного элемента a, т.е.
Подставив в (3.4) соответствующие значения, получим
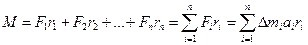
Рис. 3.3
Зная связь между линейным угловым ускорением ε ( 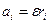
М = 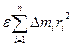
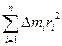
I – момент инерции тела относительно неподвижной оси.
Тогда мы получим
Или в векторном виде
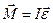
Это уравнение является основным уравнением динамики вращательного движения. По форме оно сходно с уравнением II закона Ньютона. Из (3.10) момент инерции равен
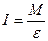
Таким образом, моментом инерции данного тела называется отношение момента силы к вызываемому им угловому ускорении. Из (3.11) видно, что момент инерции является мерой инертности тела по отношению к вращательному движению. Момент инерции играет ту же роль, что и масса при поступательном движении. Единица измерения в СИ [I] = кг·м 2 . Из формулы (3.7) следует, что момент инерции характеризует распределение масс частиц тела относительно оси вращения.
Итак, момент инерции элемента массы ∆m движущегося по окружности радиусом r равен
Для тела содержащего n элементов
I= 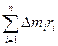
В случае непрерывного распределения масс сумму можно заменить интегралом
где интегрирование производится по всей массе тела.
Отсюда видно, что момент инерции тела зависит от массы и её распределения относительно оси вращения. Это можно продемонстрировать на опыте (рис.3.4).
Рис. 3.4
Два круглых цилиндра, один полый (например, металлический), другой сплошной (деревянный) с одинаковыми длинами, радиусами и массами начинают одновременно скатываться. Полый цилиндр, обладающий большим моментом инерции, отстанет от сплошного.
Вычислить момент инерции можно, если известна масса m и ее распределение относительно оси вращения. Наиболее простой случай – кольцо, когда все элементы массы расположены одинаково от оси вращения (рис. 3.5):
I = 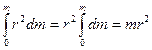
Рис. 3.5
Приведем выражения для моментов инерции разных симметричных тел массой m.
1.Момент инерции кольца, полого тонкостенного цилиндра относительно оси вращения совпадающей с осью симметрии.
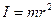
r – радиус кольца или цилиндра
2.Для сплошного цилиндра и диска момент инерции относительно оси симметрии
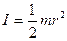
3. Момент инерции шара относительно оси, проходящей через центр
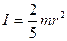
4. Момент инерции тонкого стержня длинной l относительно оси, перпендикулярной стержню и проходящей через его середину
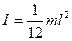
l – длина стержня.
Если ось вращения не проходит через центр масс, то момент инерции тела относительно этой оси определяется теоремой Штейнера.
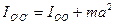
Согласно этой теореме, момент инерции относительно произвольной оси О’O’ ( 
Рис. 3.6
Кинетическая энергия вращения
Рассмотрим вращение абсолютно твердого тела вокруг неподвижной оси ОО с угловой скоростью ω (рис. 3.7). Разобьем твердое тело на n элементарных масс ∆mi. Каждый элемент массы вращается по окружности радиуса ri с линейной скоростью 
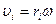
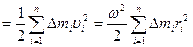
Рис. 3.7
Вспомним по (3.13), что 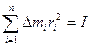
Таким образом, кинетическая энергия вращающегося тела
Ек = 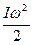
Мы рассмотрели кинетическую энергию вращения вокруг неподвижной оси. Если тело участвует в двух движениях: в поступательном и вращательном движениях, то кинетическая энергия тела складывается из кинетической энергии поступательного движения и кинетической энергии вращения.
Например, шар массой m катится; центр масс шара движется поступательно со скоростью u (рис. 3.8).
Рис. 3.8
Полная кинетическая энергия шара будет равна
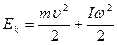
3.4. Момент импульса. Закон сохранения
момента импульса
Физическая величина равная произведению момента инерции I на угловую скорость ω, называется моментом импульса (моментом количества движения) L относительно оси вращения.
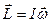
Продифференцировав уравнение (3.24) по времени, получим
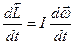
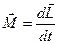
где, М – суммарный момент внешних сил. В изолированной системе момент внешних сил отсутствует (М=0) и
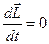
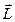
Полученный результат представлен собой закон сохранения момента импульса (момента количества движения): момент импульса (момент количества движения) замкнутой системы является величиной постоянной.
При поступательном движении системы внутренние силы не могут изменить ни импульса системы, ни ее массы, поэтому скорость центра масс остается неизменной.
При вращательном движении внутренние силы могут изменить распределение масс, а значит, момент инерции относительно оси вращения. Следствием этого должно быть изменение угловой скорости вращения тела
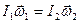
1. Фигурист на коньках изменением положения рук, регулирует свой момент инерции, а, следовательно, и скорость вращения своего тела.
2. Спортсмен, когда делает сальто, поджимает к туловищу руки и ноги, чтобы уменьшить момент инерции и увеличить угловую скорость.
3.5. Аналогия между поступательным
и вращательным движением
Если сопоставить соотношения между величинами, характеризующими поступательное движение, с такими же соотношениями для вращательного движения вокруг оси, увидим аналогию между ними. Достаточно запомнить пять соотношений между величинами поступательного и вращательного движениям (см. таблицу), чтобы перейти от описания одного вида движения к другому.
| Поступательное движение | Вращательное движение |
Путь S Скорость 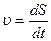 Ускорение Ускорение 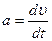 Масса m Сила F Масса m Сила F | Угол поворота φ Угловая скорость 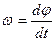 Угловое ускорение Угловое ускорение 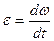 Момент инерции I Момент силы M Момент инерции I Момент силы M |
Формальной заменой указанных величин в формулах поступательного движения можно получить формулы применительно к вращательному движению.

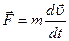
Ek= 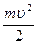
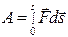
К началу
К следующей лекции К содержанию
Видео:1.142Скачать

Зависимость кинетической энергии и радиуса окружности
2017-05-20 
Кинетическая энергия частицы, движущейся по окружности радиуса $R$, зависит от пройденного пути $s$ по закону $T = as^$, где $a$ — постоянная. Найти силу, действующую на частицу, в зависимости от $s$.
Дифференцируя уравнение (1) по времени
Следовательно, искомое ускорение частицы
Следовательно, искомая сила $F = mw = 2as sqrt<1 + (s/R)^>$
📸 Видео
Кинетическая и потенциальная энергияСкачать

Урок 125. Работа, мощность и кинетическая энергия при вращательном движенииСкачать

Кинетическая энергия🤔 экзамен физика ЕГЭ и ОГЭСкачать

ПОТЕНЦИАЛЬНАЯ энергия | КИНЕТИЧЕСКАЯ энергияСкачать

В чем разница потенциальной и кинетической энергии ? Простыми словамиСкачать

Момент инерцииСкачать

Теорема Кенига, кинетическая энергия тела | Олимпиадная физика, механика | 9, 10, 11 классСкачать

Парадокс кинетической энергии ● 1Скачать

Вращательное движение. 10 класс.Скачать

Зависимость кинетической энергии от скорости и массыСкачать

Механическая работа и энергия. Кинетическая энергия. 3 часть. 9 класс.Скачать

Урок 118. Потенциальная энергия гравитационного взаимодействия. Вторая космическая скоростьСкачать

При исследовании зависимости кинетической энергии фотоэлектронов от частоты падающего света - №28514Скачать

Задача на теорему об изменении кинетической энергииСкачать