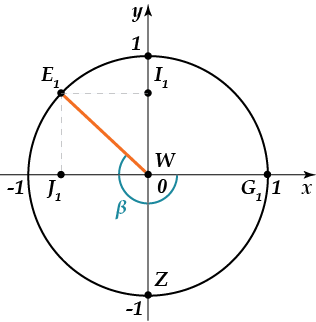Как найти координату точки на единичной окружности (8 видео)

Теория: 06 Вычисление координат точки на единичной окружности

На единичной окружности отмечена точка (displaystyle A ) как показано на рисунке. Угол (displaystyle BOA ) равен (displaystyle color ) Найдите абсциссу точки (displaystyle A )

Абсцисса точки (displaystyle A) равна Перетащите сюда правильный ответ .

Так как отрезок (displaystyle AB) перпендикулярен оси (displaystyle rm OX) то абсцисса точки (displaystyle A) равна длине отрезка (displaystyle OB)

Найдем длину отрезка (displaystyle OB)

Рассмотрим прямоугольный треугольник (displaystyle AOB) катетом которого является отрезок (displaystyle OB)

Гипотенуза (displaystyle OA) треугольника (displaystyle AOB) является радиусом единичной окружности.

Значит, (displaystyle OA=1)

Тогда, поскольку (displaystyle OB) – катет, прилежащий к углу (displaystyle color) то

Таким образом, получаем:

абсцисса точки (displaystyle A) (displaystyle = OB=cos(color))

Содержание

Тригонометрический круг: вся тригонометрия на одном рисунке
А теперь подробно о тригонометрическом круге:
Тригонометрия
💡 Видео

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.

Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .

И синус, и косинус принимают значения от до .

Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.

Знаки синуса, косинуса, тангенса и котангенса.

Синус — функция нечётная, косинус — чётная.

Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать

Тригонометрия

Найти координаты точки на единичной окружности, полученной поворотом точки ( Aleft( 1;0 right) ) на ( -225^circ ) .

Окружность единичная с центром в точке ( left( 0;0 right) ) , значит, мы можем воспользоваться упрощёнными формулами:

( beginx=cos beta =cos (-225^circ )\y=sin beta =sin (-225^circ )end ) .

Можно заметить, что ( -225^circ =-360^circ +135^circ ; -225^circ =-180^circ -45^circ ) . Изобразим рассматриваемый пример на рисунке:

Радиус ( <_>W ) образует с осью ( x ) углы, равные ( 45^circ ) и ( 135^circ ) . Зная, что табличные значения косинуса и синуса ( 45^circ ) равны ( displaystyle dfrac<sqrt> ) , и определив, что косинус здесь принимает отрицательное значение, а синус положительное, имеем:

Подробней подобные примеры разбираются при изучении формул приведения тригонометрических функций в теме «Формулы тригонометрии».

Таким образом, искомая точка имеет координаты ( left( -dfrac<sqrt>;dfrac<sqrt> right) ) .